Accelerazione di gravità sulla superficie terrestre
L’accelerazione di gravità è l’accelerazione, solitamente indicata col simbolo g, con cui cadono, in assenza di aria, tutti i corpi che si trovano sulla superficie terrestre.
In prossimità della superficie della terra il valore di g=9,8 con una buona approssimazione.
L’accelerazione di gravità determina la forza-peso, che è la forza con cui la Terra attrae un corpo.
Se indichiamo $F_p$ la forza-peso ed m la massa di un corpo, si ha
$F↖{→}_p=m⋅g↖{→}$
Con questa scrittura, viene specificato che sia $F_p$ che $g$ sono grandezze vettoriali.
Se vogliamo trovare la forza-peso del nostro corpo dobbiamo pesarci su una bilancia, individuando così la nostra massa in kg. Ad esempio, se la bilancia restituisce 70kg la nostra forza peso è data dalla formula
$F_p=70⋅9,8=686\; N$
L’accelerazione di gravità $g↖{→}$ non è costante (come G) ma dipende dalla distanza che un corpo ha dal centro della terra.
Assimiliamo la Terra a una sfera piena omogenea di massa M. Dall’equazione di Newton
$$F={GMm}/r^2$$
abbiamo l’intensità della forza di gravità che agisce su una particella di massa m posta all’esterno della Terra ad una generica distanza r dal suo centro.
Se lasciamo libera la particella, la forza di gravita F la fa cadere verso il centro della Terra con
un’accelerazione $a_g$, che chiameremo accelerazione gravitazionale.
Applicando la seconda
legge di Newton possiamo scrivere, a riguardo dei loro moduli
$$F=m⋅a_g=m⋅({GM}/r^2)$$
In quest’ultima formula $F=m⋅a_g$ rappresenta la forza-peso di un corpo di massa m ad una generica distanza r dal centro della Terra. Si tratta, dunque, della forza di gravità con cui la Terra attrae tale massa quando la massa m si trova ad una distanza r, in genere diversa dalla distanza R della superficie terrestre dal suo centro.
La legge di gravitazione universale permette di ottenere , come caso particolare, la forza-peso che descrive la gravità in prossimità della superficie terrestre cioè in corrispondenza della distanza R dal centro della terra.
$$g={GM}/R^2$$ (•)
Tramite l’esperimento
di Cavendish è stato possibile ricavare il valore della
massa della terra
$M=5,97⋅10^24\;kg$
il raggio della Terra
$R=6,37⋅10^6\;\;m$
e la costante universale di gravità
$$G=6,67⋅10^{-11}\;\; {Nm^2}/{kg^2}$$
inserendo tali valori nell’equazione (•) otteniamo
$$g=9,8\;\;m/s^2$$
Il valore di g non dipende dalla massa m del corpo; perciò nello stesso punto due corpi di massa diversa cadono con la stessa accelerazione g.
L’accelerazione di gravità, in un punto della superficie terrestre, dipende dalla distanza del punto dal centro della Terra.
Dato che la terra non è perfettamente sferica, l’accelerazione di gravità g varia da punto a punto sulla superficie terrestre.
In particolare, man mano che ci si allontana dalla superficie terrestre la distanza dal centro della Terra aumenta e l’accelerazione di gravità diminuisce. In alta montagna, il valore di g è minore che a livello del mare.
La formula di g può essere applicata per calcolare l’accelerazione di gravità sulla superficie di qualunque pianeta di cui si conosca raggio e massa.
Esempio :
la massa di Marte è $6,4⋅10^23$ kg e raggio $3,4⋅10^6$ m. L’accelerazione di gravità sulla superficie di Marte vale:
$$g=GM/R^2=6,67⋅10^{-11}{6,4⋅10^23}/{(3,4⋅10^6)^2}=3,7\;m/s^2$$
Esempio :
la massa della Luna è $7,3⋅10^22$ kg e il suo raggio è $1,7⋅10^6$ m. L’accelerazione di gravità sulla superficie della luna vale
$$g=GM/r^2=6,67⋅10^{-11}{7,3⋅10^22}/{(1,7⋅10^6)^2}=1,6\;m/s^2$$
La seguente tabella riporta alcuni valori di g calcolati per diverse altitudini rispetto alla superficie terrestre.
| Altitudine (km) | g (m/s2) | Esempio |
| 0 | 9,83 | Livello del mare |
| 8,8 | 9,80 | Monte Everest |
| 36,6 | 9,71 | Pallone aerostatico |
| 400 | 8,70 | Orbita terrestre |
| 35.700 | 0,225 | Orbita satellitare |
Fin qui abbiamo considerato la Terra come un sistema di riferimento inerziale ignorando la sua rotazione su se stessa. Questa semplificazione ci permette di considerare l’accelerazione di gravita g bene o male costante su tutta la superficie terrestre.
In realtà l’accelerazione di gravita g misurabile differisce da quella, calcolata per tre ragioni:
- perché la Terra non è omogenea;
- perché non è perfettamente sferica;
- perché la Terra, rispetto a un riferimento inerziale, gira.
Dipendenza di g dalla omogeneità della Terra
La Terra non è omogenea. La massa volumica (densità) della Terra è variabile radialmente e la densità della crosta terrestre (il guscio più esterno) della Terra è diversa nelle diverse aree della superficie terrestre. Pertanto g varia da regione a regione.
Dipendenza di g dalla sfericità della Terra
Come è stato accennato la Terra non è sferica. La forma della Terra si avvicina a quella di un ellissoide, appiattito ai poli e dilatato all’equatore.
Il raggio equatoriale supera quello polare di 21 km. Spostandosi infatti dall’equatore verso i poli, sempre a livello del mare, ci si avvicina al centro della Terra e quindi g per questo motivo crescerebbe. Un punto in vicinanza di un polo si trova pertanto più vicino al nucleo centrale ad alta densità rispetto a un punto situato sull’equatore.
Ci si può quindi aspettare che l’accelerazione di gravità g vada aumentando se ci spostiamo, a livello del mare, dall’equatore ai poli.
Dipendenza di g dalla rotazione della Terra
La Terra gira e l'asse di rotazione passa per i poli nord e sud della Terra. Un oggetto situato sulla superficie terrestre a qualsiasi latitudine salvo che ai poli ruota su una circonferenza intorno a quell’asse di rotazione ed è pertanto soggetto a un’accelerazione centripeta diretta verso il centro del circolo su cui viaggia. Questa accelerazione centripeta richiede l’esistenza di una forza centripeta, anch’essa diretta verso il centro di quel cerchio.
Per renderci conto del fatto che questo terzo requisito porta come conseguenza che l’accelerazione di gravita effettiva g differisca dall’accelerazione (teorica) gravitazionale g, e che il peso sia diverso dalla forza gravitazionale, analizziamo una semplice situazione, quella di una massa m posta all’equatore.
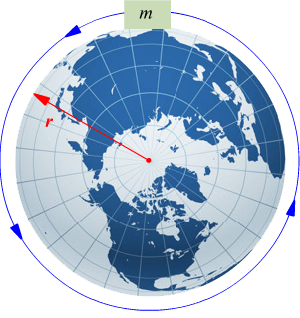
Lo schema seguente un diagramma delle forze relativo alla massa.
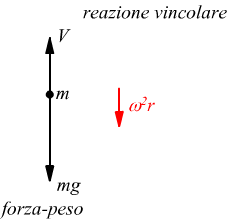
Le due forze che agiscono su di essa sono dirette radialmente lungo l’asse r che si estende dal centro della Terra. La superficie terrestre esercita sulla massa una forza normale V, diretta verso l’esterno nel verso positivo di r.
La Terra esercita sulla massa una forza gravitazionale rappresentata dal suo equivalente mg, diretta verso l'interno. Dato che la massa si muove su una traiettoria circolare attorno al centro della Terra, è soggetta a un’accelerazione centripeta che sappiamo uguale a $ω^2r$ con r raggio del cerchio (pari a circa il raggio della Terra) e ω velocita di rotazione terrestre.
Applicando alla massa la seconda legge di Newton possiamo scrivere
$V-mg=m(-ω^2r)$
L’intensità di V, è uguale al peso mg' della massa: sostituendolo a V nell’equazione precedente ricaviamo
$mg’=mg-mω^2r$
che conferma che il peso mg' della cassa è uguale all’intensità mg, della forza gravitazionale che agisce sulla cassa meno il prodotto della massa per l’accelerazione centripeta. Il peso misurato è effettivamente inferiore al modulo della forza gravitazionale, a causa della rotazione terrestre.
$g’=g-ω^2r$
da quest’ultima relazione si deduce che l’accelerazione di gravità che si riscontra in una caduta libera è effettivamente inferiore all’accelerazione gravitazionale calcolata in modo convenzionale; ciò a causa della rotazione terrestre.
Argomenti correlati:
 edutecnica
edutecnica