Leggi di Keplero
Nel XVII secolo lo scienziato tedesco Giovanni Keplero organizzò le accurate osservazioni astronomiche del suo predecessore, il danese Tycho Brahe sulla base delle idee del polacco Nicolò Copernico.
Il modello di Copernico prevedeva che il sole fosse al centro del sistema solare e che i pianeti eseguissero traiettorie circolari attorno ad esso..
Keplero dovette correggere questa ipotesi ammettendo che le orbite descritte dai pianeti attorno al sole non sono circonferenze ma ellissi.
Keplero arrivò allora alla formulazione di tre leggi empiriche che davano un notevole credito al sistema eliocentrico copernicano descrivendo la cinematica dei pianeti in modo che fosse in accordo con le osservazioni.
Le tre leggi di Keplero sono le seguenti:
- Legge delle Orbite.
I pianeti descrivono orbite ellittiche di cui il sole occupa uno dei fuochi. - Legge delle aree.
Il vettore posizione di ogni pianeta rispetto al sole descrive aree uguali della sua orbita ellittica in tempi uguali. - Legge dei periodi.
Il rapporto tra il cubo del semiasse maggiore dell’orbita e il quadrato del periodo di rivoluzione è lo stesso per tutti i pianeti $T^2/ a^3= k\;\; (cost.)$.
Le tre leggi di Keplero sono considerate empiriche, cioè sono state ricavate come leggi sperimentali ma sono perfettamente deducibili alla luce della legge di gravitazione universale
$$F=G{Mm}/r^2$$
La prima legge di Keplero è una considerazione sulla geometria delle orbite planetarie.
Nel seguente disegno si vede un pianeta di massa m che percorre un’orbita ellittica attorno al Sole.
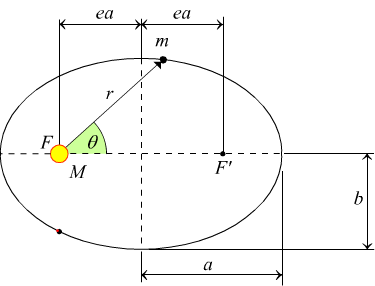
Il Sole, di massa M, si trova in F, uno dei fuochi dell’ellisse: l’altro fuoco F’ è chiamato «vuoto».
Ciascun fuoco si trova
a una distanza ea dal centro: il fattore numerico e rappresenta l’"eccentricità dell’ellisse. Sull’ellisse sono indicati il
semiasse maggiore a, e il semiasse minore b.
L’eccentricità zero definisce una circonferenza, nella quale i due fuochi coincidono in un unico punto.
Le eccentricità dei pianeti sono tanto piccole che le orbite, disegnate in scala, non si distinguono a occhio da circonferenze: per renderla evidente, l’eccentricità dell’orbita disegnata nella figura precedente è 0,75, mentre quella dell’orbita terrestre è soltanto 0,0167.
La seconda legge di Keplero è chiamata anche legge delle aree.
Nel disegno seguente schematizziamo un’orbita planetaria rispetto al sole S che occupa uno dei due fuochi dell’ellisse.
Mettiamo in evidenza il perielio P che è la posizione di minima distanza dal sole e l’afelio A che è la massima distanza dal sole.
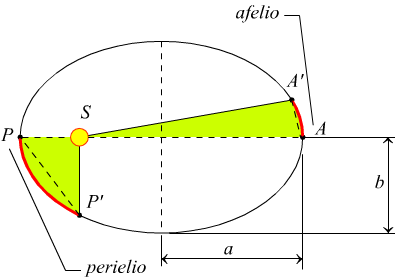
In questo schema i triangoli SPP' ed SAA' hanno la stessa area e dunque sono spazzati nello stesso tempo; questo significa che gli archi AA' e PP' sono percorsi nello stesso tempo: il pianeta è più veloce in PP' e più lento in AA’.
In termini qualitativi, questa seconda legge significa che il pianeta si muove più lentamente quanto è più lontano dal Sole, e più rapidamente quanto più è vicino al Sole.
Dimostriamo ora che la seconda legge di Keplero è perfettamente equivalente alla legge di conservazione del momento angolare. L’area dello spicchio ombreggiato nella figura seguente
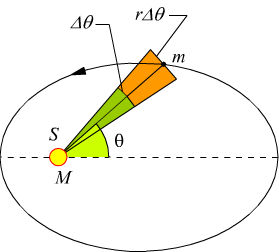
equivale quasi esattamente all’area
coperta nel tempo Δt da un segmento che collega il Sole al pianeta, separati dalla distanza r.
L’area ΔA dello spicchio è praticamente uguale all’area di un triangolo con base rΔθ e altezza r.
Si ha quindi
$$ΔA≅1/2r^2Δθ$$
Questa espressione di ΔA diventa sempre più esatta quando
Δt, e con esso Δθ tende a zero.
La rapidita istantanea con la quale viene descritta l’area è espressa da
$${dA}/{dt}=1/2r^2{dθ}/{dt}=1/2r^2ω^2$$
dove ω è la velocità angolare del segmento rotante che congiunge il pianeta al Sole.
La figura seguente
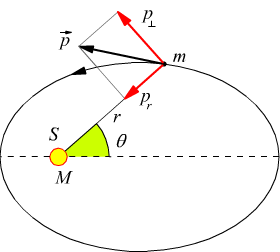
presenta il vettore quantita di moto $p↖{→}$ del pianeta, con le sue componenti. Sappiamo che l’intensita del momento angolare $L↖{→}$ del pianeta rispetto al Sole è data dal prodotto di $r↖{→}$ per la componente di $p↖{→}$ perpendicolare a $r↖{→}$, ossia, per un pianeta di massa m,
$L=rp_{⊥}=r(mv_{⊥})=r(mωr)=mr^2ω$
eliminando $ωr^2$ tra le due precedenti relazioni avremo:
$${dA}/{dt}=L/{2m}$$
Se ${dA}/{dr}$ è costante, come affermato da Keplero, ecco che l'eq.precedente conferma che anche L deve essere costante: è la legge di conservazione del momento angolare.
La terza legge di Keplero viene chiamata anche legge dei periodi. Consideriamo un’orbita circolare, che è comunque un caso particolare di ellisse con raggio r della circonferenza equivalente al semiasse maggiore dell'ellisse. Applicando la seconda legge di Newton, $F = ma$ nella legge di gravitazione universale
$$F=G{mM}/r^2$$
tenendo conto dell’accelerazione centripeta $a_c=ω^2r$ rotteniamo
$$mω^2r=G{mM}/r^2$$
sapedo che
$$ω={2π}/T$$
con T periodo del moto planetario troviamo infine la terza legge di Keplero, detta anche legge dei periodi.
$$T^2=({4π^2}/{GM})r^3$$ terza legge di Keplero
la quantità fra parentesi è una costante, il cui valore dipende soltanto dalla massa del corpo centrale.
L'equazione precedente è valida anche per orbite ellittiche, purché si sostituisca ad r il valore a del semiasse maggiore. In sostanza, il rapporto $T^2/a^3$ ha lo stesso valore per ogni orbita planetaria.
Argomenti correlati:
 edutecnica
edutecnica