Legge di gravitazione universale
La legge di gravitazione universale è una legge fisica formulata da Isaac Newton nel 1687, che descrive la forza di attrazione gravitazionale tra due corpi con massa. Secondo questa legge, la forza di attrazione gravitazionale tra due corpi è direttamente proporzionale al prodotto delle loro masse e inversamente proporzionale al quadrato della distanza che li separa.
L’uomo del passato era consapevole di essere attirato spontaneamente verso il basso (specialmente quando cadeva inciampando...), ma si immaginava che questa fosse una proprietà naturale e unica della Terra, piuttosto che di tutti i corpi, e nemmeno sapeva che fosse alla base del moto apparente dei corpi celesti.
Fu nel 1665 che il ventitreenne Isaac Newton si rese conto che tale forza era responsabile del moto lunare attorno alla Terra e dimostrò che ogni corpo dell’Universo attrae ogni altro corpo.
Questa tendenza dei corpi ad avvicinarsi prende il nome di gravitazione e la «sostanza» coinvolta nel fenomeno è la massa dei corpi.
La descrizione del comportamento di questa forza si basa tutt’oggi sulla formulazione del 1687 di Isaac Newton ciò nonostante la natura della forza gravitazione rimane ancora in parte incompresa.
Legge di gravitazione di Newton
La legge di gravità di Newton può essere enunciata nel seguente modo.
Due masse qualsiasi, di dimensioni trascurabili rispetto alla loro distanza, si attirano reciprocamente con una forza diretta secondo la loro congiungente, direttamente proporzionale alle masse stesse ed inversamente proporzionale al quadrato della loro distanza.
$$F=G{{m_1m_2}/r^2}\;\;\;\;[N]$$
dove m1 e m2 sono le masse delle due particelle e r la loro distanza.
La costante di gravitazione G è una costante universale che vale
$$6,67⋅10^{-11}\;\;\;\;\; {Nm^2}/{kg^2}$$
Secondo tale legge, l'attrazione gravitazionale è una proprieta
generale dei corpi.
Le azioni gravitazionali fra due
corpi sono mutue, cioè si presentano in coppia azione-reazione.
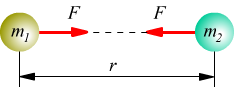
Nel disegno precedente $F↖{→}$ è un vettore che rappresenta la forza gravitazionale esercitata sulla particella di massa $m_1$ dalla particella di massa $m_2$ che per il principio di azione-reazione (terza legge della dinamica) corrisponde alla forza gravitazionale sulla massa $m_2$ esercitata da $m_1$. La forza è orientata come la retta congiungente le due masse, e si tratta di una forza di tipo attrattivo.
Il vettore $F↖{→}$ si può descrivere come avente la direzione dell’asse $r↖{→}$ che si estende dalla particella $m_1$ alla $m_2$ o, in modo più generico, definendo un vettore unitario, (o versore) orientato e diretto come l’asse $F↖{→}$, di modulo 1, tale che sia $|r↖{→} / r| = 1$, in cui $r↖{→}$ rappresenta di il vettore posizione della particella 2 rispetto alla 1 .
Possiamo quindi riscrivere la la legge di gravitazione universale in forma vettoriale nel seguente modo:
$$F↖{→}=G{m_1m_2}/r^2⋅r↖{→} / r$$
Fra tutte le forze esistenti, la forza di gravità può essere caratterizzata innanzitutto dalla sua universalità.
Tutti i corpi posseggono una massa, definita come il rapporto fra la forza applicata a essi e l'accelerazione che ne risulta. La forza di attrazione gravitazionale fra due corpi qualsiasi dipende
da entrambe le loro masse, essendo proporzionale al prodotto delle
due masse in questione.
Inoltre la forza di gravita è governata dalla legge dell’inverso dei quadrati;
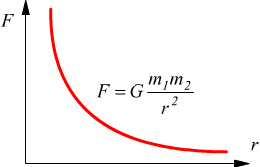
quindi la forza diminuisce molto rapidamente al crescere della distanza.
Dalla formulazione della legge si deduce che l'attrazione fra due corpi è indipendente da ciò che può esserci nello spazio compreso: una dimostrazione di ciò si ha considerando l’effetto che le varie parti della terra hanno su un corpo (sul suo peso).
Sono infatti ugualmente importanti nel determinare la forza risultante le parti vicine e quelle lontane della terra, altrimenti il teorema di Newton verrebbe a cadere.
Un’ulteriore dimostrazione si ha osservando l’orbita terrestre in corrispondenza alle eclissi solari: il passaggio delle luna fra sole e terra non produce alcuna variazione sull’orbita e quindi non altera la forza fra sole e terra. In altre parole non esistono schermi per la gravità.
Deduzione della legge di gravitazione
Newton comprese che la legge delle aree di Keplero, secondo la quale il raggio vettore che unisce il pianeta al sole copre aree uguali in tempi uguali, implica che ogni variazione di velocità Δv di un pianeta deve essere diretta sempre verso il sole.
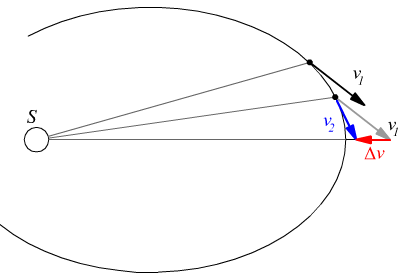
La variazione di velocità è l’accelerazione.
Dunque ogni pianeta ha una accelerazione costantemente diretta verso il sole.
Per la prima legge di Keplero, i pianeti percorrono orbite ellittiche intorno al sole, che occupa uno dei due fuochi.
Per semplificare, possiamo assumere che tali orbite siano circolari, col sole che occupa il centro; chiamiamo r il raggio.
La seconda legge di Keplero afferma che il raggio vettore posizione di ogni pianeta rispetto al sole, descrive aree uguali della sua orbita in tempi uguali.
Se l’area di un cerchio vale $A=πr^2$ essendo associata ad un settore circolare di 2π , l’area di un settore circolare descritto da un angolo θ vale
$$A=1/2θ\,r^2$$
derivando rispetto al tempo
$${dA}/{dt}=1/2r^2{dθ}/{dt}=1/2r^2ω$$
La costanza della velocità di variazione dell’area implica la costanza della velocità angolare &omega.
Questo vuol dire che il pianeta sta viaggiando di moto circolare uniforme con accelerazione centripeta $a_n=ω^2r$.
Chiameremo $m_p$ la massa del pianeta ed $m_s$ la massa del Sole.
In base alla seconda legge della dinamica il pianeta sarà soggetto ad una forza
$$F_p=m_pa_n=m_pω^2r=m_p({2π}/T)^2r$$
con T periodo di rivoluzione.
Per la terza legge di Keplero avremo $T^2=k_pr^3$; in questo modo avremo
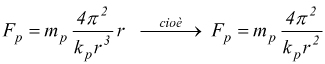
il risultato mette in evidenza come la forza esercitata dal sole sul pianeta è inversamente proporzionale al quadrato della distanza dal Sole.
Se ci collocassimo in un sistema di riferimento solidale col pianeta, vedremmo che il Sole compie un moto circolare uniforme attorno al pianeta con periodo T=24 ore.
Allora, anche per il Sole deve valere una formula analoga:
$$F_s=m_s{4π^2}/{k_s r^2}$$
Poi, per il principio di azione e reazione, le due forze devono essere uguali in modulo, $F_s=F_p$; dunque $m_sk_p=m_pk_s$.
$m_s k_p=m_p k_s$
poi è possibile definire la costante G
$$G={4π^2}/{m_p k_s}={4π^2}/{m_s k_p}\;⟶\;4π^2=Gm_pk_s$$
avremo
$$F_s=m_s{Gm_pk_s}/{k_sr^2}=G{m_p m_s}/r^2$$
ed è da questa uguaglianza che si ottiene dunque la costante di gravità G.
$$G=m_s{4π^2}/{k_s r^2}=m_p{4π^2}/{k_p r^2}$$
avremo quindi che il modulo della forza gravitazionale sole-pianeta è
$$F=G{m_p m_s}/r^2$$
e la direzione è quella della retta congiungente i due corpi.
Newton ne trasse tre conclusioni una delle quali era già stata prevista da Galileo.
In base alla prima, l’azione del sole costringe i pianeti a modificare continuamente la loro velocità, e questa variazione deve essere soggetta a leggi relativamente semplici.
Principio di sovrapposizione per la gravitazione
Dato un gruppo di particelle, possiamo trovare la forza gravitazionale risultante esercitata su ciascuna di esse applicando il principio di sovrapposizione.
Si tratta di un
principio generale che afferma che l’effetto risultante è dato dalla somma dei singoli effetti.
In questo caso ciò implica che dobbiamo calcolare la forza gravitazionale che ciascuna delle altre particelle esercita, a turno, sulla particella da noi considerata. Per trovare la forza risultante basta fare la somma vettoriale di queste singole forze.
Per n particelle interagenti il principio di sovrapposizione si può scrivere così:
$F_1=F_{12}+F_{13}+F_{14}+...+F_{1n}$
In questa espressione $F_1$ è la forza netta che agisce sulla particella 1; quanto alle altre diremo, a titolo di esempio, che $F_{14}$ rappresenta la forza netta esercitata sulla particella 1 dalla particella 4.
Questa equazione può essere espressa in forma più compatta come una sommatoria di vettori:
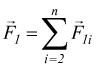
Esempio :
Dato il sistema costituito da tre particelle con masse $m_1 =6$ kg
ed $m_2 = m_3 =4$ kg, con d = 2 cm.
Qual è la forza di gravità
netta $F_1$ esercitata su $m_1$ dalle altre masse?
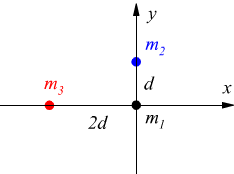
La forza $F_1$ cercata è la risultante delle due forze $F_12$ ed $F_13$ che le due particelle di massa $m_2$ e di massa $m_3$ esercitano sulla massa $m_1$.
La direzione di ciascuna delle forze gravitazionali agenti sulla particella 1 è diretta secondo la congiungente
tra quest’ultima e la particella considerata.
Siccome queste forze non giacciono su un solo asse, non possiamo sommare semplicemente le loro intensità, ma dobbiamo ricorrere a un’addizione vettoriale.
In modulo avremo
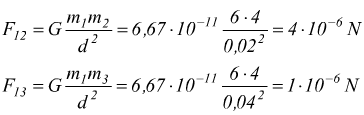
La direzione di queste due forze è qui sotto illustrata.
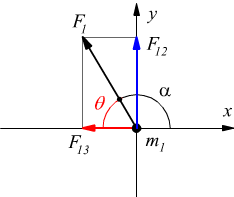
da cui si deduce
$$θ=arctg F_{12}/ F_{13}= arctg 4/1 ≃76°$$
Con l’angolo α formato dalla risultante $F_1$ con la direzione positiva dell’asse x pari a
$α=180°-θ=180°-76°=104°$
Argomenti correlati:
 edutecnica
edutecnica