Massa inerziale e gravitazionale
La massa gravitazionale caratterizza la capacità di un corpo di attirare gravitazionalmente altri oggetti e di essere attirato da essi.
La massa inerziale, invece, misura la difficoltà di un corpo ad essere accelerato.
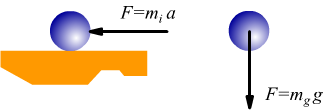
Gli esperimenti mostrano che la massa gravitazionale di un corpo è direttamente proporzionale alla sua massa . Per questo motivo alle due grandezze è stata assegnata la stessa unità di misura.
Sappiamo che ogni corpo materiale possiede una proprietà, l'inerzia, per cui una azione esterna è richiesta per alterare il suo stato di quiete o di moto (rettilineo uniforme).
Si e’ visto che vale la relazione $F =m⋅a$.
In esperienze analoghe di questo tipo la gravitazione,
in genere, non ha nulla a che vedere; se per esempio si considera un corpo su un piano orizzontale privo di attrito la forza (F) necessaria a dare una certa accelerazione orizzontale sarebbe la stessa nel caso reale ed in quello in cui la gravitazione non fosse presente.
La massa così introdotta è la massa inerziale $m_i$.
La seconda situazione è quella gravitazionale, il fatto cioè che i corpi si attraggono reciprocamente con una forza data dalla legge di Newton nella quale intervengono le masse. Per l'intensità vale la formula:
$$F=G{m_{g1} m_{g2}}/r^2$$
In questo caso l’inerzia sembra non rientrare.
Noi possiamo applicare una forza uguale e contraria e tenere il corpo in
quiete sotto l’azione della forza da noi applicata e della gravitazione,
oppure possiamo lasciarlo cadere verso la terra con moto accelerato. Le
masse che intervengono a descrivere il comportamento dei corpi nei riguardi
della gravitazione, vengono chiamate masse gravitazionali
$m_g$.
Nello scrivere in precedenza la legge della gravitazione noi abbiamo usato il simbolo generico di massa (m) come se le masse inerziali e gravitazionali dei corpi coincidessero. Si pone ora la domanda: questo è vero?
Consideriamo due corpi A e B portati ad interagire con un terzo corpo C alla stessa distanza da esso. Le forze di gravitazione hanno le intensità:
$$F_{AC}=G{m_{gA} m_{gC}}/r^2$$
$$F_{BC}=G{m_{gB} m_{gC}}/r^2$$
ed il loro rapporto
$$ F_{AC}/ F_{BC}= m_{gA}/ m_{gB}$$
Se il terzo corpo è la terra, le forze sono i pesi
$$p_A/p_B= m_{gA}/ m_{gB}$$ (•)
cioè la legge di gravitazione universale contiene implicitamente l’asserzione che i pesi dei vari corpi, allo stesso posto della terra,sono proporzionali alle loro masse gravitazionali.
D'altra parte per gli stessi corpi (A e B) è possibile determinare le masse inerziali con esperienze nelle quali non interviene la gravitazione.
Allora si può pensare di lasciare cadere i corpi sotto l’azione della gravità: tutte le esperienze di questo genere hanno mostrato che l’accelerazione di gravità (nel vuoto), è in un certo
punto sempre la stessa qualunque sia la massa inerziale dei
corpi. Il moto è causato in questi casi dalle forze di gravitazione
(peso) e si può scrivere per il II° principio della dinamica:
$\{\table p_A=m_{iA}g ; p_B=m_{iB}g $
$$p_A/p_B= m_{iA}/ m_{iB}$$ (★)
In altre parole i pesi dei corpi in un punto della terra stanno esattamente come le loro masse inerziali.
Il confronto fra (★) e (•) mostra che le masse inerziali dei corpi risulterebbero essere proporzionali alle masse gravitazionali.
Per giudicare meglio questa relazione Newton ricorse ad un esperimento. Se si riprende l’equazione del pendolo semplice distinguendo fra masse inerziali e masse gravitazionali si ha
$$ml{d^2θ}/{dt^2}=-m_ggsinθ$$
Risolvendo l’equazione differenziale si otterrebbe allora un periodo pari a
$$T=2π√ {{m_il}/{m_gg}}$$
che sì riduce a
$$T=2π√ {l/g}$$
solo se $m_i =m_g$.
Newton, costruì allora, un pendolo formato da un involucro nel quale poteva porre diverse sostanze. Egli sperimentò ponendo nell’involucro successivamente corpi diversi che avevano lo stesso peso (determinato con una bilancia) e quindi la stessa $m_g$.
Tutto il resto (anche la resistenza dell’aria, l’ampiezza
di oscillazione) era nelle successive esperienze mantenuto costante.
Una qualsiasi differenza in accelerazione, e quindi in T,si sarebbe dovuta imputare all’essere diverse le masse inerziali
per i vari corpi.
Newton peraltro non riuscì a mettere
in evidenza alcuna variazione di periodo e concluse che si può
porre $m_i =m_g$.
Il metodo usato da Newton non consente una precisione molto elevata.
Solo nel 1909 il fisico ungherese Eotvos realizzò un dispositivo sperimentale in grado di rivelare differenze nelle forze di gravitazione con una precisione di una parte su 100.
La proporzionalità fra $m_g$ ed $m_i$; controllata con grande precisione, ha successivamente permesso di porre pari ad 1 il loro rapporto e di ritenere equivalenti le masse inerziali e gravitazionali.
Ciò fra l’altro, rende possibile misurare le masse (inerziali) mediante pesate (con la bilancia) nelle quali si paragonano le forze peso che sollecitano corpi diversi nello stesso posto. La coincidenza delle masse inerziali e gravitazionali è, in meccanica classica ritenuta una fortunata coincidenza, mentre trova una sua logica spiegazione nella teoria generale della relatività: non si tratta di due diverse proprietà della materia, ma di due differenti aspetti di una unica e fondamentale caratteristica di tutta la materia.
Argomenti correlati:
 edutecnica
edutecnica