Gravità
L'esperimento di Cavendish è un esperimento scientifico condotto da Henry Cavendish nel 1797 per misurare la densità della Terra e calcolare la costante di gravitazione universale.
L'esperimento si serviva di una bilancia di torsione per misurare la forza di attrazione gravitazionale tra due masse sferiche di piombo. Attraverso questo esperimento, Cavendish fu in grado di determinare con precisione la densità della Terra e la costante di gravitazione universale G.
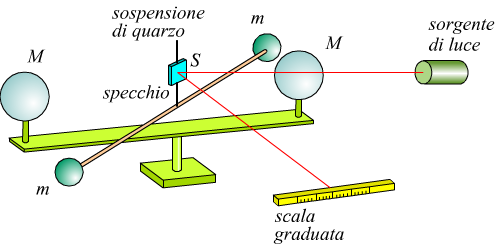
Il disegno precedente mostra la costituzione di una bilancia di torsione. Un sottile e lungo filo, avente una estremità fissata ad un supporto, porta all'altra estremità un equipaggio formato da un’asta rigida orizzontale e due masse uguali (m) di forma sferica. Il sistema costituisce una bilancia di torsione: applicando una coppia all'equipaggio si osserva una rotazione θ dell'asta intorno all’asse verticale.
La nuova posizione di equilibrio si raggiunge quando la coppia di reazione elastica (dovuta alla torsione del filo e proporzionale a θ) eguaglia la coppia applicata. La conoscenza delle caratteristiche elastiche del filo e la determinazione di θ consentono di valutare il momento della coppia applicata.
La determinazione di θ puo farsi fissando all’asta uno specchio S che viene illuminato da
un fascio parallelo di luce proveniente da una sorgente L.
Il
fascio riflesso e rilevato su una scala graduata.
L'esperienza, dunque, consiste nel porre due altre masse sferiche M, ciascuna ad uguale distanza da una delle masse m e nel misurare la coppia applicata all’equipaggio e dovuta alle forze attrattive fra le due coppie di masse m ed M.
Per far ciò si possono montare le due sfere M su una sbarra rigida che puo ruotare intorno ad un asse verticale che coincide con il filo della bilancia di torsione. Si possono allora fare due misure con le masse M nella posizione A e B .
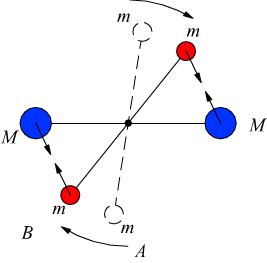
L’esperienza è delicata perché le forze di attrazione in gioco sono piccole. Se per esempio si considerano due masse sferiche (m ed M) di 100 kg ciascuna, ad un metro di distanza l'azione attrattiva risulta $6,670⋅10^{-7}$ N.
Essendo le forze cosi piccole, precauzioni devono essere prese per evitare azioni disturbatrici.
I risultati delle esperienze introdotti nella legge di gravitazione universale consentono la determinazione di G.
Per questa costante si trova il valore:
$$G=6,67⋅10^{-11}\;\;\;\;\; {Nm^2}/{kg^2}$$
La determinazione di G consente il calcolo della massa della terra (si dice alle volte che Cavendish determinando G ha pesato la terra).
Se infatti si considera il peso di un corpo di massa m, esso rappresenta la forza di attrazione fra corpo e terra (massa M).
$$F=mg=G{mM}/R^2$$
chiamiamo R, distanza fra massa m e centro della terra considerata sferica e formata da involucri sferici uniformi,e il raggio della terra $R=6,37⋅10^6$ m ; $g=9,8 m/s^2$ l'accelerazione di gravità sulla superficie della terra. Risulta
$$M=R^2g/G=5,97⋅10^24\;\;\;kg$$
La densità media della terra si ottiene dividendo tale valore per il
volume della terra.
Si ottiene una densità media di $5500 kg/m^3$ cioè
circa 5,5 volte quelle dell'acqua.
Siccome la densità media della crosta terrestre, formata essenzialmente da rocce, è notevolmente più bassa, $(2000÷3000 {kg}/m^3)$ si deve concludere che la densità media nell’interno della terra (al di sotto della crosta) e notevolmente superiore a $5500 {kg}/m^3$.
La legge di gravitazione, nota la massa della terra, consente di calcolare la massa del sole.
Se si considera il moto della terra intorno al sole, e per un calcolo grossolano si assume circolare la traiettoria con un raggio $R_{TS}=1,5⋅10^11\;m$ (determinato con osservazioni astronomiche) si puo' porre la forza di attrazione pari alla massa della terra per l'accelerazione centripeta:
$$G{M_T M_S}/R_{TS}^2=M_Tv^2/ R_{TS}$$
La velocità v con cui la terra percorre la sua orbita è
$$v=2πR_{TS}/T$$
essendo T un anno solare
$$v={6,28⋅1,5⋅10^11}/{3,156⋅10^7}=2,99⋅10^4\;m/s$$
dunque
$$M_S={v^2R_{TS}}/G={(2,99⋅10^4)^2(1,5⋅10^11)}/{6,67⋅10^{-11}}=2,01⋅10^30\;\;kg$$
cioe’ circa 300.000 volte la massa della terra.
Argomenti correlati:
 edutecnica
edutecnica