Energia potenziale gravitazionale
Il campo gravitazionale è un campo di forze conservativo.
Un campo di forze si dice conservativo quando il lavoro compiuto da esso su una particella dipende solo dalla posizione iniziale e finale della particella e non dal percorso seguito per raggiungere la posizione finale.
L'energia potenziale è una forma di energia che un oggetto possiede a causa della sua posizione ed è associata alla configurazione di un sistema in cui agiscono forze conservative, come nel caso del campo gravitazionale .
Quando una forza conservativa svolge un lavoro L su un corpo entro un sistema, la variazione ΔU di energia potenziale del sistema è
Energia potenziale gravitazionale della forza peso
In prossimità della superficie terrestre, dove possiamo ritenere costante l’accelerazione di gravità $g=9,81\;m/s^2$, applichiamo la definizione appena data.
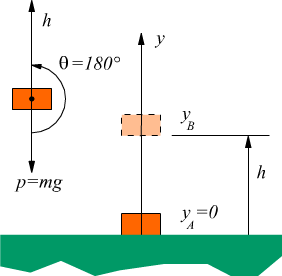
Supponiamo di dover sollevare una massa m da un punto A ad un punto B, avremo
$ΔU=U_B-U_A=-L_{AB}$
dove $L_{AB}$ è il lavoro da compiere per portare il corpo dal punto A al punto B.
La variazione di energia potenziale gravitazionale di un corpo è uguale al lavoro compiuto dalla forza-peso quando il corpo stesso si porta dalla posizione iniziale a quella finale.
Per definizione il lavoro è il prodotto scalare della forza applicata per lo spostamento effettuato, che in questo caso chiamiamo h.
$L_{AB}=F⋅h=Fhcosθ$
nel nostro caso è $F=mg$ : forza-peso della massa. Dal disegno si vede $θ=π=180°$ ne consegue $cosθ=-1$, avremo allora $L_{AB}=-mgh$.
La variazione di energia potenziale vale allora :
$ΔU=mgh$
Da queste considerazioni si traggono le seguenti conclusioni.
L'energia potenziale gravitazionale è l'energia associata alla posizione di un oggetto rispetto a una sorgente di gravità, come ad esempio la Terra.
Questa energia dipende dall'altezza dell'oggetto rispetto al punto di riferimento scelto e si manifesta quando l'oggetto si muove verso il basso a causa della forza di gravità.
In pratica, maggiore è l'altezza dell'oggetto, maggiore è la sua energia potenziale gravitazionale.
Energia potenziale gravitazionale nello spazio
Se le approssimazioni precedenti non sono valide, cioè se non siamo in prossimità della superficie terrestre e non possiamo ritenere valida la condizione g=cost. allora dobbiamo attuare un approccio più rigoroso che prevede l’uso della formula generale
$$ΔU=- ∫_{x_i}^{x_f}F(x)dx$$
dove
$x_i$ = punto iniziale di partenza
$x_f$ = punto finale di arrivo
In tal caso è possibile dimostrare che l’energia potenziale gravitazionale di due particelle, di due masse m e M, separate da una distanza r, può essere espressa dalla seguente espressione:
$$U=-{GMm}/r$$ (★)
Supponiamo che una pallina da tennis venga lanciata in aria come per allontanarla verticalmente dalla superficie terrestre (come indicato nel seguente disegno).
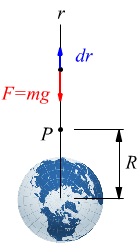
Questa pallina viene lanciata verticalmente verso l’alto e
passa per il punto P posto a distanza R dal centro della Terra.
Nel disegno Sono indicati la
forza gravitazionale F agente sulla pallina e un vettore spostamento differenziale
$dr↖{→}$, entrambi diretti lungo l’asse radiale r.
Calcoliamo il lavoro L svolto dalla forza di gravita sulla pallina durante il suo spostamento dalla posizione iniziale nel punto P a una posizione lontanissima, a distanza infinita. Dato che la forza gravitazionale F(r) è una forza variabile (e dipende da r), per esprimere il lavoro dobbiamo ricorrere alla formula iniziale
$$L=- ∫_{R}^{∞}F↖{→}(r)dr↖{→}$$
Il prodotto scalare tra la forza e lo spostamento differenziale può essere sviluppato in questo modo
$$F↖{→}⋅dr↖{→}=F(r)drcosθ=-{GMm}/r^2dr$$
perché $θ=180$ e $cosθ=-1$. Integrando:
$$L=- ∫_{R}^{∞}F↖{→}(r)dr↖{→}=GMm∫_{R}^{∞}{dr}/r^2=0-{GMm}/r$$
Dunque
$$L=-{GMm}/R$$
L qui rappresenta il lavoro richiesto per spostare la pallina dal punto P (posto a distanza R) all’infinito. Con l’equazione iniziale (ΔU = — L) possiamo anche scrivere il lavoro in termini di energia potenziale come
$U_∞-U=-L$
L’energia potenziale all’infinito ($r=∞$) vale zero e U è l’energia potenziale nel punto P. Si conclude che
$$U=L=-{GMm}/R$$
quindi, per un generico valore della distanza R ritroviamo la (★).Ricordiamo che la forza gravitazionale è una forza conservativa. Dunque il lavoro svolto dalla forza di gravitazione su una particella nel corso di un suo spostamento fra due punti non dipende dal percorso seguito dalla particella, ma soltanto dalle sue posizioni iniziale e finale. 11 lavoro è uguale e di segno opposto alla differenza di energia potenziale fra i due punti:
$L=-ΔU=-(U_f-U_i)$
ove $U_f$ e $U_i$ sono i valori dell’energia potenziale associata rispettivamente alla posizione finale e a quella iniziale della particella. E, dato che il lavoro L svolto da una forza conservativa è indipendente dal percorso, la variazione di energia potenziale gravitazionale $ΔU$ è pure indipendente dal particolare cammino seguito.
Argomenti correlati:
 edutecnica
edutecnica