Filtri  

      

I filtri sono particolari quadripoli, funzionanti in regime alternato che si comportano in modo selettivo rispetto alle frequenze di funzionamento a cui sono soggetti.
Quando si parla di filtri elettronici, bisogna fare una distinzione fra filtri passivi e filtri attivi. Se si definisce col termine A il rapporto fra la tensione di uscita e la tensione di ingresso al filtro elettronico, si avrà

Questo significa che i filtri attivi sono circuiti amplificatori del segnale, mentre i filtri passivi, attenuano il segnale. Infatti dalle relazioni precedenti risulta che nel caso dei filtri attivi, il segnale di uscita ha una ampiezza maggiore del segnale di ingresso mentre in un filtro passivo il segnale di uscita sarà minore o al più uguale al segnale di ingresso.

Il filtri passivi possono essere costruiti con semplici componenti passivi cioè resistenze condensatori e induttanze. Per fabbricare un filtro attivo, invece, bisogna poter disporre almeno di un componente attivo: Amplificatore operazionale, transistor, JFET...etc. (oltre a vari ed eventuali componenti passivi).

I filtri attivi , come abbiamo visto, sono in genere, studiati usando la nozione di funzione di trasferimento , perchè usando come strumento matematico la Trasformata di Laplace risulta più semplice l'analisi della risposta nel tempo, mentre l'utilizzo dei diagrammi di Bode semplifica la rappresentazione grafica nel dominio della frequenza. I filtri passivi, sono inquadrati ( con qualche deroga) nello stesso modo.
E' possibile una trattazione anche senza questi strumenti ma l'analisi matematica e grafica dei sistemi considerati potrebbe risultare più difficoltosa e meno rigorosa.

Adottando queste modalità operative, dobbiamo solo ricordarci che stiamo considerando dei sistemi lineari, in generale, funzionanti in regime variabile. Non siamo mai certi di che natura sia il segnale in ingresso: potrebbe essere costante potrebbe essere periodico, potrebbe essere armonico (sinusoidale). Per queste ragioni viene usata la pulsazione generalizzata e complessa s=σ+jω ; attraverso essa vengono definite per il condensatore la :

Reattanza capacitiva che solo in alternata diventa

per l'induttore la

Reattanza induttiva che solo in alternata diventa

Le resistenze rimangono dei numeri reali.
Se in un filtro il segnale di ingresso è periodico, il segnale di uscita avrà lo stesso periodo, quindi uscita ed ingresso hanno la stessa frequenza e la stessa pulsazione.

In tutti i tipi di filtri, attivi o passivi, viene studiato il legame fra l'attenuazione A_v=V_o/V_i al variare della pulsazione ω ( e quindi della frequenza ).

Filtri passivi

      

I filtri passivi si individuano in tre tipologie:

passa basso, se lasciano libero transito alle basse frequenze, bloccando quelle alte;
passa alto, se lasciano libero transito alle alte frequenze, bloccando quelle basse;
passa banda, se lasciano libero transito ad un gruppo di frequenze intermedie, bloccando quelle alte e quelle basse.

Filtro RC passa basso

      

E' costituito dalla serie di una resistenza R e di una capacità C, come indicato. La funzione di trasferimento vale

essa presenta un polo reale negativo per     

I diagrammi asintotici di Bode sono illustrati in figura

Applicando in ingresso un segnale sinusoidale di ampiezza V_iM costante,l'ampiezza del segnale sinusoidale in uscita è uguale a quella dell'ingresso ( 0 dB equivale a |A_v| =1 )
per valori di ω inferiori a

Viceversa per ω > ω_p, l'ampiezza di V_o si riduce via via sempre più e |A_v| diminuisce di 20dB/dec. In modo qualitativo si può giungere alle stesse conclusioni, facendo alcune considerazioni direttamente sul circuito.
Infatti per ω=0 (cioè in continua), la reattanza di C risulta infinita (circuito aperto), in questo modo v_i si trasferisce integralmente in uscita e V_oM=0 e quindi e |A_v|_dB= - ∞.

Ritornando ai diagrammi di Bode, si vede che per ω > ω_p, il modulo A_v in decibel vale -3db e quindi, non espresso in decibel,   .

Lo sfasamento fra uscita e ingresso è circa nullo a frequenze basse, per le quali la trasmissione del segnale non è influenzata ancora dalla capacità, mentre raggiunge -90° a frequenze elevate, quando l'effetto capacitivo diviene predominante.

Per la sua caratteristica di privilegiare la trasmissione delle frequenze basse (sostanzialmente inferiore a ω_p ), il circuito viene detto filtro passa-basso. In regime sinusoidale l'attenuazione diventa:

La frequenza di taglio ricordando che

In questa rappresentazione della risposta in frequenza, si constata che:

• per ω=0 si haV_o/V_i=1 cioè V_o=V_i, la tensione di uscita è uguale alla tensione di ingresso, il quadripolo è trasparente e il segnale applicato passa indisturbato;
• per ω → ∞ si ha V_o/V_i → 0 cioè V_o→0 la tensione di uscita tende a zero, il quadripolo diviene opaco e il segnale applicato non passa; o come si vede dalla figura:

• per 0 < ω < ∞ il segnale tende ad essere attenuato, poco alla frequenze basse, molto alle frequenze alte, conferendo al quadripolo il comportamento tipico di un filtro passa basso.

Il limite fra la banda passante e la banda oscura è fissato convenzionalmente per quel valore di pulsazione in cui il rapporto di attenuazione diviene che si ha in corrispondenza del polo come si è detto.

Il modulo e la fase della f.d.t. valgono in base alle uguaglianze precedenti

Filtro RC passa alto

      

Si ottiene scambiando fra di loro R e C, come illustrato la funzione di trasferimento A_v(s) vale

Presenta uno zero nell'origine ( il numeratore si annulla per s=0 ) e un polo reale negativo per

             Ponendo l'equazione s=jω si ottiene

Per costruire i diagrammi di Bode basta sommare i diagrammi elementari relativi a uno zero nell'origine e a un polo reale negativo; occorre però tenere presente che, per il modulo, la presenza della costante τ_p al numeratore trasla il diagramma relativo allo zero, spostandone l'intersezione con l'asse ω nel punto 1/τ_p anziché 1. Infatti 0 dB corrisponde ora a ωτ_p=1.

Una giustificazione qualitativa del comportamento del filtro può essere fatta esaminando direttamente il circuito. infatti per ω=0, il condensatore apre il collegamento ingresso-uscita e V_oM=0
( e quindi |A_v|_dB=- ∞ ).
Viceversa per ω → ∞ , il condensatore C tende a cortocircuitare l'uscita con l'ingresso, sicché V_oM=V_iM e |A_v|=1 ( 0 dB ). L'effetto capacitivo, prevalente alle basse frequenze, determina per V_o un anticipo di fase di 90°, che si riduce via via al crescere di ω.

La frequenza di taglio inferiore f_L, nell'equazione precedente, si ottiene dividendo numeratore e denominatore per jωτ_p e passando alla variabile f:

Modulo e fase possono essere espressi come

In questo caso si definisce frequenza di taglio inferiore f_L a 3 dB la frequenza per la quale il modulo assume il valore e scende quindi di 3 dB rispetto al suo valore alle alte frequenze. Pertanto la f_L coincide con la frequenza d'angolo f_p e si ha:

Dopo queste considerazioni, risulta semplice progettare un filtro RC passa-alto o passa-basso.

R Ω kΩ MΩ

C µF nF pF

In ogni caso si trova la pulsazione del polo ω_p che corrisponde alla frequenza di taglio superiore f_H del filtro passa-basso oppure la frequenza di taglio superiore f_L del filtro passa alto.

Filtro RL passa basso

      

E' costituito dalla serie di un'induttanza L e di una resistenza R. La funzione di trasferimento vale

    

Presenta un polo per s = p = -R/L = -1/τ_p ( dove τ_p è la costante di tempo associata al polo). La funzione di trasferimento è del tutto simile a quella del filtro passa-basso RC e simili risultano quindi i diagrammi del modulo e della fase. Per la frequenza di taglio superiore a 3 dB si ha:

Filtro RL passa-alto

      

Viene ottenuto da quello passa-basso scambiando le posizioni R e L . La funzione di trasferimento risulta

E presenta uno zero nell'origine ( z=0 ) e un polo per s = p = -R/L = -1/τp Questa equazione è simile a quella vista per il filtro passa-alto RC, per cui i diagrammi sono gli stessi. La frequenza di taglio inferiore a 3 dB risulta :

Anche per i filtri RL un esame diretto del circuito, basato sul comportamento dell'induttanza alle basse e alle alte frequenze (opposto a quello di una capacità), permette di prevedere qualitativamente le loro caratteristiche di trasmissione.

Anche per i filtri di tipo RL è facile calcolare la frequenza di taglio

R Ω kΩ MΩ

L mH µH

essa corrisponde alla pulsazione dell'unico polo. Ma questo, come si comprende, è valido solo quando abbiamo a che fare con un sistema del I° ordine. Non sempre si ha a che fare con un polinomio del I° ordine al denominatore della f.d.t.

Filtro passivo passa banda

      

E' possibile costruire un filtro passa banda passivo utilizzando i circuiti ed i componenti precedenti, ad es. usando resistenze e condensatori, secondo questo schema a blocchi:

La funzione di trasferimento del filtro passa alto sarebbe       

La funzione di trasferimento del filtro basso alto sarebbe   

La funzione di trasferimento complessiva del filtro passa banda è

Già sappiamo che il filtro passa alto ha un polo per   

Mentre il filtro passa basso ha un polo per   

Possiamo intuire come la risposta in frequenza complessiva sia il risultato della sovrapposizione delle due risposte parziali.

Volendo un filtro che abbia una risposta come questa

per il passa alto abbiamo scelto

per il passa basso abbiamo scelto

Filtro passivo arresta banda

      

E' possibile costruire un filtro arresta banda, utilizzando solo componenti passivi, combinando i circuiti precedenti

Non ci dilunghiamo ancora perchè il circuito risultante è già stato visto ed è conosciuto come rete a sella.

Filtri di banda (circuiti risonanti)

      

I filtri di banda noti anche come 'circuiti risonanti', sono particolarmente usati come nella trasmissione dei segnali, una loro trattazione senza l'utilizzo della pulsazione complessa s è già stato fatto in elettrotecnica. Questi filtri,possono essere di tipo serie o parallelo.

Circuito risonante serie

      

E' costituito da tre elementi R, L e C disposti in serie, come illustrato. Considerando come grandezza di uscita la corrente I (s), si può scrivere:

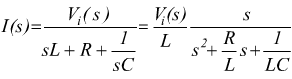
La funzione di trasferimento I(s)/Vi(s) presenta uno zero nell'origine e due poli.
Infatti al denominatore si nota un trinomio di secondo grado nella variabile s: i poli potranno dunque essere complessi coniugati, reali coincidenti o reali distinti, ma queste eventualità sono già state intraviste nei filtri attivi di II^o ordine:
Il diagramma del modulo parte allora con pendenza iniziale (basse frequenze) di 20 dB /dec, a causa dello zero nell'origine, per passare a -20 dB /dec alle alte frequenze dopo l'intervento dei due poli.
Ci si deve aspettare un andamento selettivo della risposta in frequenza, con attenuazione sia alle basse sia alle alte frequenze. Passando al regime sinusoidale s=jω si può scrivere:

                  se si pone

   

Si ha Z( jω)=R cioè l'impedenza Z( jω) diviene puramente resistiva. Inoltre in corrispondenza di ω_o il modulo di Z(jω) è minimo e quindi la corrente I è massima ( e in fase con V_i ) e vale

La pulsazione ω_o prende il nome di pulsazione di risonanza con la corrispondente frequenza di risonanza

       alla risonanza la reattanza induttiva è uguale alla reattanza capacitiva    

inoltre, alla risonanza, le tensioni del circuito valgono

     [#]

Q viene chiamato coefficiente di risonanza e vale               

Esprime il rapporto fra la reattanza di L o C alla risonanza e la resistenza R ed è tanto più alto quanto più l'elemento resistivo (dissipativi) diviene trascurabile rispetto agli elementi reattivi.
Inoltre quanto più alto è Q tanto maggiori sono V_L e V_C rispetto V_i e a V_R. Nei circuiti applicativi Q è sempre maggiore di 1 a arriva spesso al centinaio.

Dall'equazione [#] si nota che alla risonanza V_i cade interamente su R, mentre V_L e V_C normalmente maggiori di V_i sono uguali fra loro in modulo ma sfasate di 180°.

Per quanto riguarda la risposta in frequenza, si ha che fuori dalla risonanza per ω< ω_o la parte immaginaria dell'impedenza Z( jω) diventa negativa, cioè predomina l'effetto capacitivo.
Ciò dipende dal fatto che, alle basse frequenze, la reattanza di C cresce mentre cala quella di L.
Viceversa alle alte frequenze ( ω > ω_o ) predomina la reattanza induttiva.
In figura è rappresentata la risposta in frequenza del modulo e della fase di I per due diversi valori di R.

L'andamento del modulo è selettivo nei confronti delle frequenze e presenta il tipico andamento a campana. centrato sulla frequenza di risonanza . Più la frequenza di V_i si discosta dalla frequenza di risonanza f_o più l'ampiezza di I e quindi delle tensioni si riduce.

R Ω kΩ MΩ

C µF nF pF

C mH µH

In questo caso, si definice banda passante l'intervallo di frequenza attorno ad f_o per cui I è superiore a
   dove I_o è il valore massimo della corrente; mentre f_L e f_H vengono rispettivamente indicate la frequenza di taglio inferiore e superiore a 3 dB. Si dimostra che la banda dipende da Q e più precisamente

Da questa relazione si deduce che quanto più è elevato Q (e quindi piccola R) tanto più stretta è la bada e quindi più selettiva la risposta in frequenza del circuito risonante. Le due frequenze di taglio non sono simmetriche rispetto a f_o, ma f_o è la media geometrica delle due, vale a dire .
Tuttavia nei circuiti applicativi, dove Q è normalmente elevato, si può considerare con buona approssimazione f_o pari alla media aritmetica fra le due frequenze di taglio e pertanto

Circuito risonante parallelo

      

E' costituito dai tre elementi R, L e C disposti in parallelo, come illustrato. Nell'analisi del suo funzionamento conviene considerarlo alimentato dal generatore di corrente I_i ( a cui può essere condotto, con l'applicazione del teorema di Norton, un eventuale generatore di tensione). In regime sinusoidale si ha

Alla risonanza. L'ammettenza Y( jω) diviene puramente resistiva e assume il suo valore minimo
( l'impedenza è quindi massima) quando

             cioè per               

Anche in questo caso ω_o prende il nome di pulsazione di risonanza.
Alla risonanza il generatore I_i vede come carico la sola R e pertanto V=RI_i . I valori delle correnti nei tre rami del circuito sono

Dove Q è il coefficiente di risonanza, che rappresenta in questo caso il rapporto fra e la reattanza di L o C alla risonanza

Il significato fisico di Q è lo stesso del circuito risonante serie; tanto più è trascurabile la componente dissipativa del circuito ( R elevata) e tanto più Q è elevato. Alla risonanza le due correnti I_Le I_C sono uguali e contrarie ( e sfasate di ±90° rispetto a I_i); pertanto nella maglia costituita da L e C circola un'unica corrente, di valore Q volte quello di I_i.

Poi abbiamo la risposta in frequenza. Nel grafico seguente sono riportate le curve di modulo e fase di V al variare di f per due valori di resistenza. Alle basse frequenze ( f < f_o ) pre domina l'effetto induttivo; infatti nel parallelo la sempre maggiore reattanza di C perde peso nei confronti della sempre minore reattanza di L. Alle alte frequenze, viceversa, predomina nel circuito risonante l'effetto capacitivo.

Anche in questo caso la banda passante, compresa fra le frequenze di taglio a 3 dB, f_L e f_H è legata al coefficiente di risonanza dalla relazione

e si può in prima approssimazione, nei casi reali, supporre f_L e f_H simmetriche rispetto a f_o.

R Ω kΩ MΩ

C µF nF pF

L mH µH