Trasformata di Laplace
La trasformata di Laplace è una operazione che si esegue sulle funzioni a variabile reale per trasformarle in funzioni a variabile complessa.
Questa operazione, contrariamente a quello che si può pensare, consente di apportare notevoli semplificazioni nei calcoli matematici.
Facciamo considerazioni solo su funzioni del tempo che sono quelle più
ricorrenti nello studio dei fenomeni fisici; quindi il tempo viene considerato
come variabile reale, indipendente, e le sue funzioni f(t) vengono
definite per t>0 considerando nulle le f(t) per t<0.
Indichiamo con s la variabile complessa s=σ+jω (pulsazione
complessa) e con F(s) la funzioni a variabile complessa.
Data una funzione f(t) reale e nulla per t<0, si definisce
trasformata di Laplace della f(t) e la si indica con:![]() la
seguente funzione
la
seguente funzione
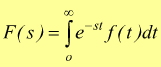
dove s=σ+jω è la pulsazione complessa.
La f(t) viene moltiplicata per il termine e-st ed integrata
rispetto a t tra i limiti![]() (
la s risulta costante rispetto al tempo t).
(
la s risulta costante rispetto al tempo t).
Nell'operazione di integrazione il tempo viene a sparire e si ottiene una funzione nella sola variabile s cioè una funzione di una variabile complessa.
1] ![]()
Si tratta della funzione a gradino unitario, quindi f(t)=1 per t>0 ed f(t)=0 per t<0.
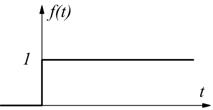
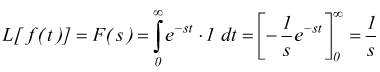
2] ![]()

4] ![]()
che è riscrivibile come 

ponendo jωt=kt come nel caso precedente. Per evitare di calcolare ogni volta la trasformata di una funzione si può far uso della tabella riportata in questa pagina.
Teoremi sulla trasformata di Laplace
1] La trasformata del prodotto di una funzione per una costante è uguale al prodotto della trasformata della funzione per la costante stessa.
![]() con
con ![]()
2] La trasformata di una somma di funzioni è uguale alla somma delle trasformate delle singole funzioni
![]()
![]()
quindi sono possibili combinazioni lineari. Teorema della linearità:
![]() con
a e b costanti.
con
a e b costanti.
3] La trasformata della derivata di una funzione è uguale ad s volte la trasformata della funzione stessa meno il valore che assume la f(t) all'istante t=0.Teorema di derivazione di f(t):
![]()
![]()
da questa formula si deduce l'espressione della trasformata di Laplace per le derivate seconda, terza, etc..
![]()
Esempio:calcolare la trasformata di Laplace di ![]() nota la regola
nota la regola 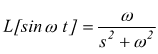
e sapendo,inoltre che  si
ottiene
si
ottiene
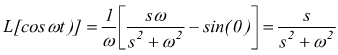
4] La trasformata dell'integrale di una funzione è uguale alla trasformata della funzione stessa divisa per s. Teorema dell'integrale:
![]()

si deduce  e
e 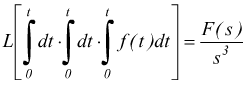

Esempio: calcolare la L[t] (funzione a rampa).
Tale funzione può essere pensata come
![]() ma
la
ma
la 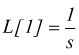 quindi
quindi

5] La trasformata di una funzione moltiplicata per t è uguale alla derivata della trasformata della funzione rispetto ad s cambiata di segno.Teorema della derivata di F(s):
![]()
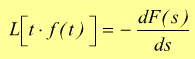 o
anche
o
anche
![]()
infatti dalla definizione di trasformata di Laplace si ha:

Esempio: calcolare la L[t2]; se pensiamo che t2=t·
t e che 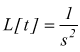 si
ha che
si
ha che
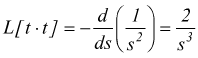
6] Teorema della traslazione:
![]()
![]()
esempio: calcola la ![]()
Sapendo che 
7] Teorema del ritardo:

Data una f(t) viene definita funzione ritardata di durata to la funzione y(t) tale che:
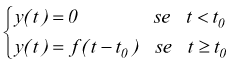
Infatti si dimostra che :
![]()
posto ![]() per
la definizione di trasformata di Laplace:
per
la definizione di trasformata di Laplace:
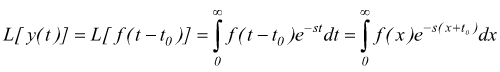
si vede che è nullo il contributo dell'integrale nell'ntervallo [0,t0] ed essendo dx=dt:
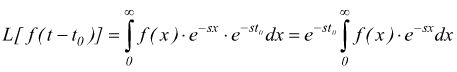 ottenendo
ottenendo
![]()
Esempio:Si abbia una funzione a gradino unitario che inizia all'istante t=t0;
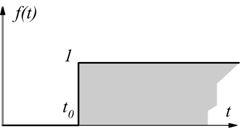

dato che la trasformata del gradino unitario (non traslato) è pari
ad 1/s,
quella a gradino traslato è pari a ![]() .
.
Questo ultimo teorema è utile per ricavare le espressioni della trasformata di alcune funzioni particolari, prendiamo ad esempio in considerazione la seguente funzione f(t) di tipo impulsivo.
La funzione impulsiva f(t) può essere scritta:
![]()

8] Trasformata di funzioni periodiche: Sia f(t) una funzione periodica di periodo T, nulla per t<0 ed f*(t) la funzione corrispondente al primo periodo.


![]()

Questa formula permette di ricavare la trasformata di Laplace di molte funzioni periodiche di interesse elettronico.





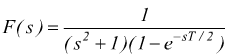
Se la F(s) non ha poli nel semipiano destro è anche possibile applicare i seguenti teoremi:
9] Teorema del valore iniziale: ![]()
10] Teorema del valore finale: ![]()
Antitrasformata di Laplace
L'operazione di antitrasformazione, consiste nel risalire da una funzione di variabile complessa , a quella di variabile reale, la cui trasformata coincide con la funzione di partenza.
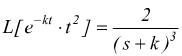 trasformata
trasformata
 antitrasformata
antitrasformata
non tutte le funzioni a variabile complessa sono antitrasformabili.
Nella teoria dei controlli automatici, la funzione da antitrasformare, può essere una relazione rappresentativa tra una causa ed un effetto , in particolare può esprimere il rapporto fra l'ingresso e l'uscita di un sistema.
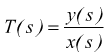

In generale la funzione di trasferimento di un sistema lineare è un rapporto fra due polinomi della variabile s:
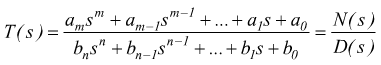
Le radici del polinomio del numeratore z1,z2,..zm
sono dette zeri e per questi valori la funzione di trasferimento si annulla.
Le radici del polinomio al denominatore p1,p2,..pn
sono dette poli e per questi valori la funzione di trasferimento vale
infinito.
Gli zeri o i poli di valore nullo sono chiamati poli e zeri nell'origine
In particolare un polo nell'origine introduce una integrazione perché,
per il teorema dell'integrale la trasformata dell'integrale di una funzione
effettua una divisione per s; uno zero nell'origine, introduce una derivazione
(per il teorema della derivata). Noti i poli e gli zeri di una f.d.t.
la T(s) può assumere due forme equivalenti dette canoniche.
1a forma canonica.

con j differenza fra il numero di poli e di zeri nell'origine.
2a forma canonica.
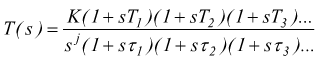
dove ![]() e
e ![]()
K=guadagno statico; è il valore della T(s) quando s=0 (supponendo j=0).
Le τi vengono dette costanti di tempo del sistema.
Nota la f.d.t. T(s) è possibile determinare la risposta y(s) ad una data
sollecitazione x(s); infatti:
![]()
Particolare importanza riveste lo studio della risposta di un sistema ad un segnale a gradino unitario con x(t)=1 e x(s)=1/s; si tratta dunque di antitrasformare l'uscita y(s) che risulta essere in definitiva una funzione razionale fratta nella variabile s.

dove N(s) è un polinomio di grado inferiore o uguale a D(s) , questo perché in un sistema reale al tendere ad infinito di s l'uscita deve tendere ad un valore finito (non può aumentare indefinitivamente). In questo contesto risulta utile scomporre la y(s) in frazioni parziali.
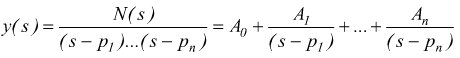
ottenendo con il metodo dei residui

A0 è nullo se il grado n del denominatore è maggiore
del grado m del numeratore.
Se m=n si ha A0=am termine noto di
N(s).
Se nella formula risulta am=bn=1 valgono
le seguenti proprietà.
A] se n≥m+2 la somma dei residui vale zero ![]()
B] se n=m+1 la somma dei residui vale 1 ![]()
Risoluzione di una equazione differenziale lineare con la trasformata di Laplace
Data l'equazione differenziale ![]() con
le condizioni iniziali:
con
le condizioni iniziali:
![]() e
e ![]()
ricavare la x(t) che soddisfi l'eq. data. Indichiamo ![]()
trasformando e applicando i teoremi [1] e [2] 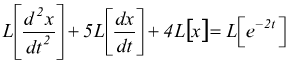
Applicando il teorema [3] si ha
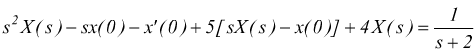
raccogliendo a fattor comune i termini in X(s) 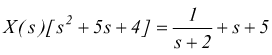 ottenendo
ottenendo 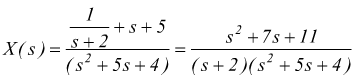
La x(t) si trova antitrasformando la X(s) 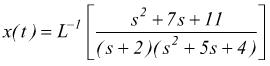 scomponendo
scomponendo
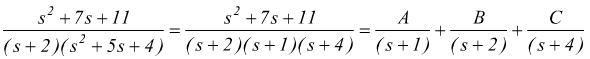
da cui si ricava 

La trasformata di Laplace , fornisce la soluzione direttamente tenendo conto delle condizioni iniziali, mentre col metodo classico occorre trovare prima la soluzione generale e poi imporre le condizioni iniziali.
Applicazione della trasformata di Laplace ai circuiti elettrici

Considerando il circuito disegnato, supponendo che alla chiusura dell'interruttore il condensatore C sia scarico ci proponiamo di scrivere la relazione che lega la corrente i(t) alla tensione applicata v(t) dal momento della chiusura dell'interruttore in poi.
 legge
di Kirchoff all'unica maglia
legge
di Kirchoff all'unica maglia
si eseguono le trasformate di entrambi i membri.

quest'ultima può essere scritta direttamente rappresentando il circuito nel modo seguente:

basta sostituire al generatore v(t) la V(s), al condensatore
la reattanza 1/sC e all'induttore la reattanza sL; la resistenza
deve rimanere invariata. Essendo la V(s) nota si può ottenere la
![]() antitrasformando.
antitrasformando.
In modo del tutto analogo sarà possibile ottenere altre grandezze di interesse. Ad es. qualora interessasse conoscere l'andamento della vL(t) applicando la regola del partitore di tensione si potrebbe ottenere:

Bisogna fare attenzione se nel circuito già esistono delle cariche iniziali sul condensatore oppure se vi sono delle correnti iniziali nelle induttanze.
Se in una induttanza circola una corrente iniziale i0, nel circuito in serie alla reattanza sL vi sarà una f.e.m. di valore Li0 , con il morsetto + nel verso positivo della i0.
Se un condensatore è inizialmente carico ad una tensione v0, occorre considerare in serie alla reattanza 1/sC una f.e.m. di valore v0/s con il morsetto + coincidente con l'armatura positiva del condensatore.
Riassumendo le regole generali per il calcolo simbolico con la trasformata di Laplace:


[a]- si sostituiscono tutti i generatori v(t)
con f.e.m. continue di valore pari alle trasformate delle v(t).
[b]- tutte le resistenze con resistenze di ugual
valore.
[c]- si sostituiscono tutte le induttanze L con
reattanze di valore sL eventualmente in serie con una f.e.m. di valore
Li0, dove i0 è la corrente iniziale nell'induttanza.
[d]- si sostituiscono tutti i condensatori di capacità
C con delle reattanze di valore 1/sC eventualmente in serie con una f.e.m.
di valore v0/s dove v0 è la tensione iniziale ai
capi del condensatore.
[e] - si considerano le correnti e le
tensioni così calcolate come le trasformate di Laplace delle effettive
grandezze.
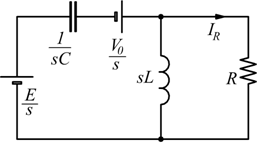
Esempio: nel circuito di figura con il condensatore inizialmente
carico alla tensione V0.
Si vuole conoscere l'andamento della corrente nella resistenza R
dal momento della chiusura dell'interruttore; coi dati:
E=40V V0=20V R=200Ω L=1,25H C=5µF
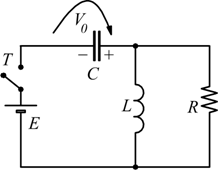
Abbiamo detto che il circuito equivalente è il seguente:
Se I(s) è la corrente che circola nella reattanza 1/sC
la corrente IR(s) sarà data dalla formula:
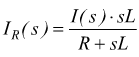
ma la I(s) sarà data dalla somma delle f.e.m. diviso l'impedenza vista dalla I(s) stessa.
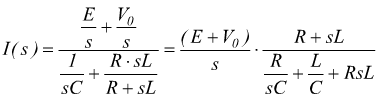 semplificando
semplificando
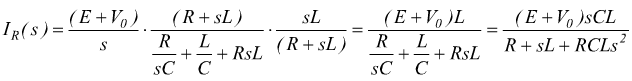
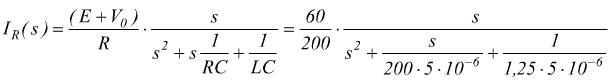

poi decomponendo in fattori

antitrasformando si ottiene ![]()
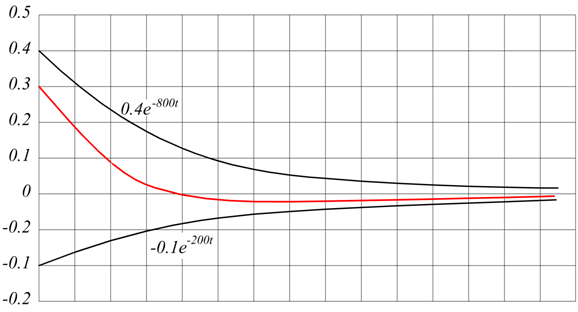
Sistemi del primo ordine
In elettronica, corrispondono formalmente ai filtri del primo ordine, di cui si è già studiata la risposta in frequenza. La funzione di trasferimento ha la forma :

mentre il segnale di ingresso a gradino x(s)=1/s. Si ha dunque:
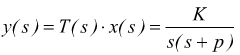 antitrasformando
antitrasformando
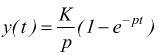

Sistemi del secondo ordine
In elettronica, corrispondono formalmente ai filtri del secondo ordine, di cui si è già studiata la risposta in frequenza. La funzione di trasferimento ha la forma :
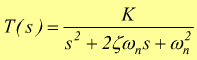
mentre il segnale di ingresso a gradino x(s)=1/s. Si ha dunque:

la sua antitrasformazione dipende dal valore dei poli del trinomio di
secondo grado al denominatore. Oltre alla pulsazione naturale ωn
, si notano lo smorzamento ζ e il fattore di merito Q con.

i poli del trinomio valgono ![]()
a] per ζ>1 i poli sono reali distinti.
b] per ζ=1 i poli sono reali coincidenti.
c] per ζ<1 i poli sono complessi coniugati.
a]
poli reali distinti; si avrà 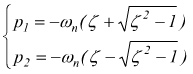
per ogni valore di ζ>1 p1 e p2 sono entrambi
reali e negativi, la risposta al gradino è:
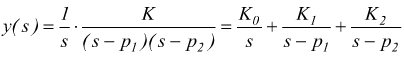 si
ha
si
ha
![]() con
con
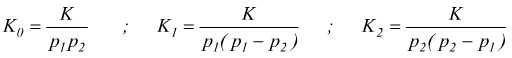 notando
che
notando
che
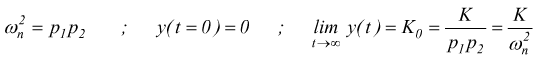
b] poli reali coincidenti : si deve avere lo smorzamento ζ=1 , il trinomio al denominatore diventa:
![]() con
con ![]()
La risposta al gradino diventa : ![]()
quast'ultima è riscrivibile come: 
notando che 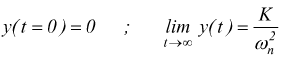
qui la risposta qualitativa per ζ≥ 1 con poli reali

c] poli complessi coniugati :
si verifica se ζ<1 , e si ha
è possibile dimostrare che la risposta al gradino è:
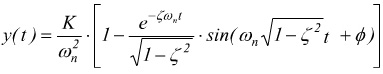

viene quantificato l'overshoot come 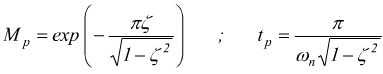
quindi all'istante tp l'uscita vale ![]()
e il tempo di salita 
qui la risposta qualitativa per ζ<1 con poli complessi coniugati

 edutecnica
edutecnica