Funzione di trasferimento e risposta in frequenza
La funzione di trasferimento è una grandezza che caratterizza i sistemi fisici lineari. Essa si può definire come il rapporto fra il segnale di uscita ed il segnale di ingresso di un dato sistema.

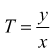
Non sempre la funzione di trasferimento può essere ricondotta ad un unico coefficiente numerico, in genere la sua espressione risulta essere più complessa e dipendente dalla variabile rispetto alla quale viene studiato il sistema (tempo, frequenza, pulsazione).
In generale per studiare una f.d.t. si usa la pulsazione complessa ![]() per
cui sia il segnale di ingresso che quello di uscita che la funzione stessa,
saranno funzione di s:
per
cui sia il segnale di ingresso che quello di uscita che la funzione stessa,
saranno funzione di s:
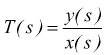
La rappresentazione della T(s) al variare di s si studia usualmente sui
diagrammi di Bode, dove sull'asse delle ordinate viene riportata la ![]() espressa
in Decibel, mentre sull'asse delle ascisse si ha ovviamente, s, essendo
una pulsazione, si misura in rad/s.
espressa
in Decibel, mentre sull'asse delle ascisse si ha ovviamente, s, essendo
una pulsazione, si misura in rad/s.
Questo significa che sulle ascisse avremo una scala di valori di questo
tipo:

L'asse delle pulsazioni è suddiviso in decadi (scala logaritmica) cioè si ha una suddivisione in ragione delle potenze del 10 (10-100-1000…rad/s).
Nel caso più generale la f.d.t. è espressa da una funzione razionale fratta del tipo:
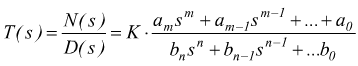 con
m≤n
con
m≤n
possiamo ricondurla alla forma:
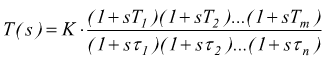
Le radici del numeratore (i valori di s che annullano il numeratore:
![]()
vengono chiamati zeri
della funzione di trasferimento.
Le radici del denominatore (i valori di s che annullano il denominatore:
![]()
vengono chiamati poli della funzione
di trasferimento.
Il modulo è espresso in dB:
![]()
La funzione di trasferimento, essendo una funzione di una variabile complessa,
restituisce sempre un numero complesso, ecco perché si parla di modulo
e fase della f.d.t.:
in regime puramente sinusoidale ![]() .
Avremo per il suo modulo:
.
Avremo per il suo modulo:
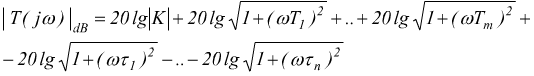
per la sua fase:
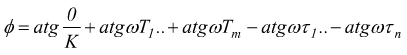 con
con 
questa ultima operazione è dovuta al fatto che dobbiamo considerare la costante K come un numero complesso del tipo K=a+jb. In tal caso la sua fase vale:
![]() ma
se la parte immaginaria b=0 si ha solo a=K cioè :
ma
se la parte immaginaria b=0 si ha solo a=K cioè : ![]()
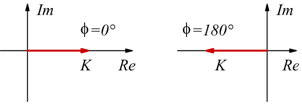
cioè i casi possibili sono quelli illustrati in figura.

Infatti, il rapporto b/a, può tendere a zero in due modi diversi:
per ![]() oppure
per
oppure
per ![]() come viene indicato in figura.
come viene indicato in figura.
Per questi scopi, è, inoltre, sempre indicato fare mente locale al grafico della funzione y=atg(x).

Funzione di trasferimento costante
![]()



Funzione di trasferimento con uno zero nell'origine
![]()
essa è assimilabile alla retta di equazione sul piano cartesiano; retta y=mx con coefficiente angolare m che passa per l'origine. Nel nostro caso il coefficiente sarà equivalente ad una pendenza di 20dB su decade di frequenza.


per s=jω (in regime sinusoidale puro):
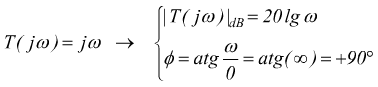
infatti, si nota come la variabile s a numeratore abbia parte immaginaria ω e parte reale 0.
Funzione di trasferimento con un polo nell'origine
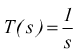

essa è assimilabile alla retta di equazione y=mx sul piano cartesiano; retta con coefficiente angolare m negativo (funzione decrescente) che passa per l'origine. Nel nostro caso il coefficiente sarà equivalente ad una pendenza di -20dB su ogni decade di frequenza.

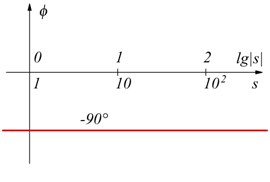
per s=jω (in regime sinusoidale puro):
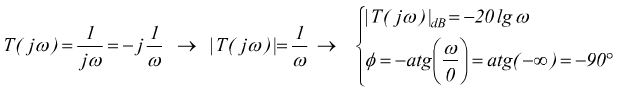
infatti, si nota come la variabile s a denominatore abbia parte immaginaria ω e parte reale 0.
Funzione di trasferimento con uno zero reale negativo
![]()
![]()
per 
Nel primo caso: s<<1/T essa è assimilabile ad una retta collocata sul piano cartesiano perfettamente sovrapposta all'asse delle ascisse.

Nel secondo caso: s>>1/T, si comporta come una retta del tipo y=mx+q con coefficiente angolare m positivo ;
nel nostro caso il coefficiente sarà equivalente ad una pendenza di 20dB
su decade di frequenza. La retta interseca l'asse delle ordinate nel punto
y=q cioè ![]()
In regime sinusoidale puro:
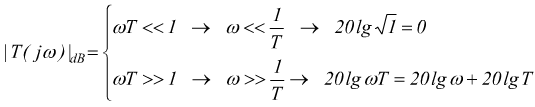
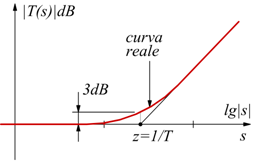

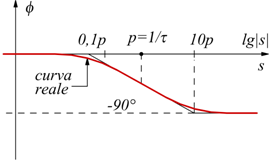
Il diagramma del modulo è, in prima battuta una spezzata poligonale (diagramma ideale) la curva reale si distingue da quella ideale in corrispondenza di eventuali poli o zeri della funzione di trasferimento.
Nel nostro caso, si vede come in corrispondenza della zero z=1/T il modulo
della funzione assume valore ![]() (3dB).
In questo punto si ha il massimo scostamento fra il diagramma reale e
quello ideale.
(3dB).
In questo punto si ha il massimo scostamento fra il diagramma reale e
quello ideale.
Anche il diagramma della fase è approssimato:
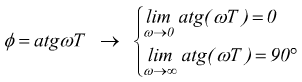
In pratica, si considera la fase uguale a 0 per valori inferiori a z/10 ed uguale a 90° per valori di s (jω ) superiori a 10 volte lo zero z
Nell'intervallo 0,1z ∼10z la pendenza è di 45° per ogni decade di frequenza.
Funzione di trasferimento con un polo reale negativo

![]()
per 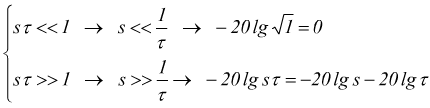
Nel primo caso: s<<1/τ la funzione è assimilabile ad una retta collocata sul piano cartesiano perfettamente sovrapposta all'asse delle ascisse. Nel secondo caso: s>>1/τ , si comporta come una retta del tipo: y=mx+q con coefficiente angolare m negativo (funzione decrescente).
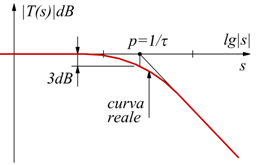
Se siamo in regime sinusoidale puro:

Esempio di costruzione di un diagramma di Bode
Ipotizziamo una f.d.t. già data nella forma:
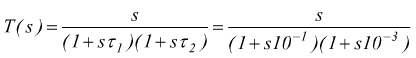
è dotata di uno zero nell'origine e di due poli reali. Per quello che riguarda il diagramma del modulo, l'elemento che troviamo alla frequenza minore è lo zero nell'origine.
z=s=0 dec=1 rad/s. Il suo contributo al diagramma è riportato in figura:

soltanto in una fase successiva (aumentando la frequenza s) incontriamo il primo polo:

preso singolarmente, la risposta in frequenza di questo polo è data in figura:

La composizione fra lo zero nell'origine e il primo polo produce il seguente risultato:

Il polo non influisce con la salita di pendenza 20dB/dec imposta dallo zero finché non si arriva alla frequenza del polo stesso, a quel punto, la salita imposta dallo zero si elide con la discesa imposta dal polo (entrambe di 20dB/dec).
Il secondo polo si presenta quando:

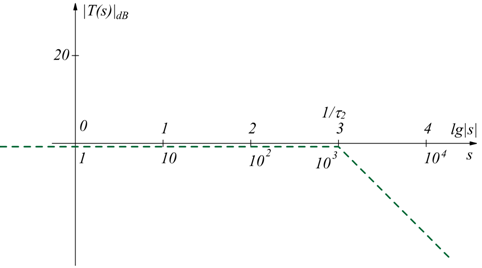
La composizione fra questo ultimo polo e il diagramma parziale che avevamo tracciato, produce il seguente risultato:

Chiaramente si tratta del diagramma ideale che approssima soltanto quello reale. I maggiori scostamenti si avranno, come si è visto, in corrispondenza dei due poli con errori di 3dB.
Per la costruzione del diagramma della fase ci avvaliamo della forma:
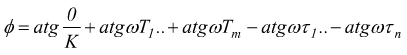 con
con 
![]()
Infatti, il primo termine (associato all'eventuale costante K) è nullo (K=1>0) mentre lo zero nell'origine introduce uno sfasamento costante di +90°. Il diagramma risultante:

 edutecnica
edutecnica