Modelli di sistemi
Il modello di un sistema è una rappresentazione schematica del sistema stesso, ne rende semplice l'analisi, sempre considerandone le funzionalità. E' rappresentabile come un blocco orientato come illustrato qui sotto:
![]()
dove x=x(t) e y=y(t) sono rispettivamente il segnale di ingresso e di
uscita, mentre T[ ] è l'operatore che deve essere applicato al segnale
di ingresso x per ottenere l'uscita y.
Possiamo ottenere l'uscita y del sistema illustrato sotto:
![]()
noi applichiamo all'ingresso l'operatore $T=5[\;]^2+3[\;]$; per cui sarà:
$T=5[x]^2+3[x]$
L'operatore T rappresenta dunque il legame funzionale fra l'ingresso e l'uscita del sistema, esso è in genere riconducibile ad una espressione matematica; come tale è rappresentabile su un piano coordinato dove la x è variabile indipendente e la y quella dipendente.
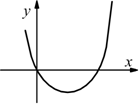
Questa curva viene solitamente chiamata transcaratteristica del sistema.
Schemi a blocchi
Un sistema fisico, raramente può essere rappresentato da un singolo
blocco funzionale, in generale esso può essere ricondotto ad in insieme
di blocchi collegati in vario modo fra loro.
L'algebra degli schemi a blocchi è l'insieme delle regole che ci può
permettere di semplificare lo schema descrittivo di partenza di un dato
sistema in una forma più semplice, sulla quale si possa operare.
Gli elementi principali da prendere in considerazione sono i seguenti:
Blocco di trasferimento
dove vale la relazione $y=A⋅x$
da cui si ottiene $$A=y/x$$
la costante A rappresenta la funzione di trasferimento del blocco.
Nodo sommatore
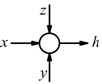
esegue il confronto fra due o più segnali fornendo in uscita la
loro somma algebrica: h=x+y+z
Punto di diramazione
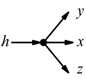
E' un nodo particolare in cui esiste una singola entrata e più uscite
legate dalla relazione: h=x=y=z
Collegamento in serie
Si ha un collegamento in serie quando il segnale di uscita di un
blocco è il segnale di ingresso del blocco successivo. Valgono le
relazioni:
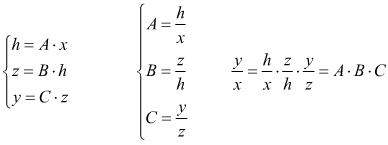
Lo schema iniziale viene così semplificato: ![]()
Collegamento in parallelo
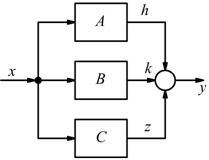
Più blocchi sono collegati in parallelo, quando hanno lo stesso
segnale di ingresso, mentre le uscite convergono verso lo stesso
nodo sommatore.
Valgono le relazioni:
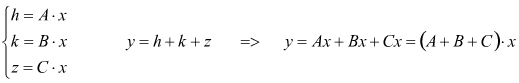
lo schema viene così semplificato: ![]()
Spostamento di un punto di
diramazione rispetto a blocchi di trasferimento
Dato il seguente schema di esempio:
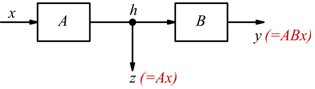
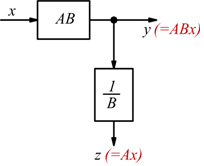
è possibile manipolare lo schema ottenendo le due seguenti possibili
soluzioni equivalenti:
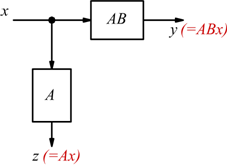
Spostamento di un nodo sommatore
E' possibile spostare un nodo sommatore lasciando invariate le uscite
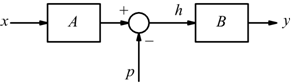
notiamo come in questo caso sia:
![]()
Spostamento del un nodo sommatore
a valle
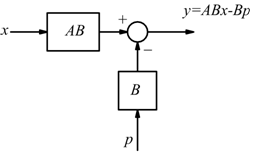
Spostamento del un nodo sommatore
a monte
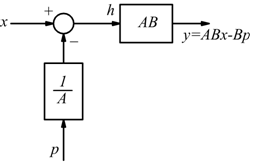
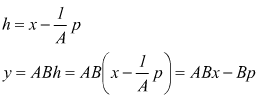
Reazione positiva
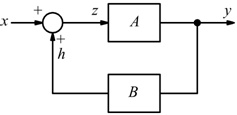
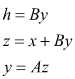

![]()
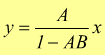
Reazione negativa
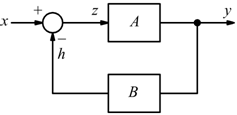
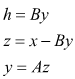
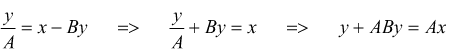
![]()
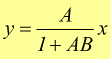
 edutecnica
edutecnica