Permutazioni

Le permutazioni di un insieme, sono i modi diversi con cui si puo indicare quell'insieme quando gli elementi dell'insieme differiscono solo per l'ordine in cui si presentano.

Una definizione generale per le permutazioni può essere la seguente:

dato un insieme di n elementi si definiscono permutazioni di n elementi (diversi tra loro) i raggruppamenti degli n elementi scelti in un ordine qualsiasi.

Quindi una permutazione differisce da un'altra solo per l'ordine degli elementi .

Dalla definizione, segue che le permutazioni coincidono con le disposizioni semplici di un insieme di n elementi di classe n.

Permutazioni semplici

Per esemplificare, ci proponiamo di costruire e contare gli anagrammi, anche privi di significato, che si possono formare con le tre lettere della parola APE.

Come si sa, gli anagrammi richiesti sono tutte le parole che si ottengono mutando solo il posto delle lettere della parola assegnata, quindi sono le disposizioni semplici delle tre lettere di APE, prese a tre a tre; ossia:

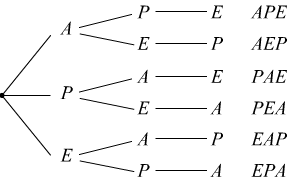
permutazioni semplici

Come si può vedere, ciascun anagramma contiene tutte le lettere assegnate e due anagrammi differiscono, l'uno dall'altro, solo per l'ordine con cui sono disposti gli elementi in essi contenuti.

Il numero di questi anagrammi è:
$D_{3,3}=3⋅2⋅1=6$
In questo caso, invece di parlare di disposizioni semplici di tre oggetti a tre a tre si preferisce parlare di permutazioni semplici e, al posto di $D_{3,3}$, si utilizza il simbolo caratteristico, $P_3$.

Un altro esempio può essere il seguente: vogliamo calcolare il numero di modi distinti con cui 30 alunni si possono disporre in un laboratorio informatico che presenta 30 postazioni.

Poiché il numero degli alunni è uguale al numero dei posti del laboratorio, allora le diverse disposizioni semplici differiranno solo per l'ordine; quindi esse sono le permutazioni semplici dei 30 alunni.

Dunque, il numero di modi diversi con cui i 30 alunni si possono permutare nel laboratorio linguistico è:

$P_{30}=D_{30,30}=30⋅29⋅28⋅... ⋅3⋅2⋅1=2,6525⋅10^32$

Questo numero enorme, uguale al prodotto:

$30⋅29⋅28⋅... ⋅3⋅2⋅1$

si indica con il simbolo: 30! che si legge 30 fattoriale, oppure fattoriale di 30.

Più in generale, il fattoriale di un numero naturale n, maggiore di uno, è uguale al prodotto:

$n!=n(n-1)(n-2)⋅..⋅2⋅1$

avremo allora
$2!=2⋅1=2$
$3!=3⋅2⋅1=6$
$4!=4⋅3⋅2⋅1=24$
$5!=5⋅4⋅3⋅2⋅1=24$
ecc..

Sembra che il punto esclamativo, che caratterizza il simbolo n! sia stato scelto dai primi studiosi di questo argomento per indicare lo stupore che essi provarono osservando la crescita rapidissima di n fattoriale al crescere di n.

Ad esempio: Dieci cavalli disputano una gara di corsa ippica.
Calcolare il numero dei possibili ordini di arrivo.
I possibili ordini di arrivo sono tanti quanti ne indica il numero delle permutazioni semplici dei 10 concorrenti; ossia:

$P_{10}=10!=10⋅9⋅8⋅... ⋅2⋅1=3.628.800$

In virtù delle precedenti osservazioni potremo dare la seguente definizione per le permutazioni semplici

Si chiamano permutazioni semplici di n oggetti distinti, le disposizioni semplici degli n oggetti dati, presi a n a n.

In altre parole, possiamo dire che:

Le permutazioni semplici di n oggetti distinti sono tutti i possibili raggruppamenti contenenti, ciascuno di essi, la totalità degli n oggetti dati, e che differiscono soltanto per l'ordine con cui sono disposti gli elementi.

Ad esempio, supponiamo che ad un concorso vi siano tre concorrenti:A,B,C in quanti modi possibili si può rappresentare la graduatoria finale? Dopo una breve analisi giungeremo alla conclusione che la graduatoria finale dovrà necessariamente essere una delle seguenti:

ABC, ACB, BAC, BCA, CAB, CBA

che sono in numero 3·2·1=6.
Se indichiamo con $P_n$ le permutazioni di un dato insieme di n elementi, avremo formalmente:

$P_n=D_{n,n}=n(n-1)(n-2)·...·1=n!$

Vediamo un ultimo ed ulteriore esempio.

Un rider deve eseguire cinque consegne a domicilio della merce acquistata da altrettanti clienti residenti ciascuno in cinque zone diverse della città.
Vogliamo calcolare il numero di differenti modi con cui il rider può eseguire le consegne.

Il rider può eseguire le consegne della merce ai rispettivi clienti in tanti modi diversi quante sono le permutazioni semplici delle cinque zone diverse della città in cui risiedono quei clienti, ossia:

$P_5=5!=5⋅4⋅3⋅2⋅1=120$

Altri argomenti correlati: