Combinazioni
Le combinazioni di un insieme possono essere definite come sottoinsiemi formati dalla scelta di un certo numero di elementi dell'insieme di partenza, senza tener conto dell'ordine in cui essi compaiono.
Dato un insieme di $n$ elementi, si dicono combinazioni semplici degli $n$ elementi di classe $k$ (con $k≤n$) i raggruppamenti di $k$ elementi, scelti fra gli $n$ dell'insieme, tali che ogni raggruppamento differisca dagli altri per la natura degli elementi (senza considerare l'ordine degli elementi).
Mentre nelle disposizioni e nelle permutazioni si tiene conto dell’ordine degli elementi, nelle combinazioni non se ne tiene conto.
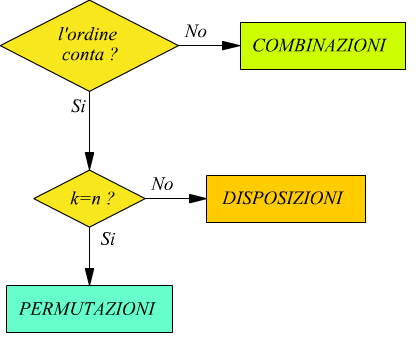
Mentre per le disposizioni si considerano diversi due raggruppamenti purché essi differiscano almeno un elemento o per l’ordine degli elementi, per le combinazioni due raggruppamenti si considerano diversi soltanto se essi differiscono per almeno un elemento.
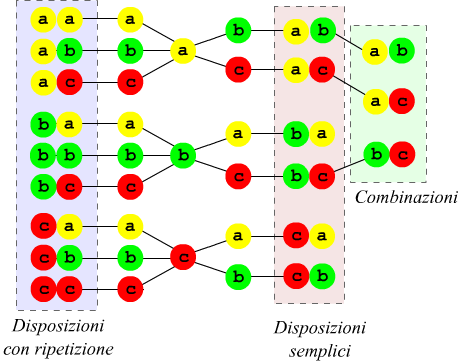
Combinazioni semplici
Un’altra definizione, più circostanziata, delle combinazioni può essere la seguente:
Dati $n$ oggetti distinti, e indicato con $k$ un numero intero positivo minore o uguale ad $n$, si chiamano combinazioni semplici di questi $n$ oggetti, presi a $k$ a $k$ (o di classe $k$), tutti i raggruppamenti diversi che si possono formare con gli oggetti dati in modo che valgano le seguenti proprietà:
- ciascun raggruppamento contiene $k$ oggetti;
- uno stesso oggetto non può figurare più volte in un raggruppamento;
- l’ordine degli oggetti non ha importanza, e quindi due raggruppamenti sono da considerarsi diversi soltanto quando differiscono tra loro almeno per un oggetto.
Il numero complessivo di combinazioni di n oggetti di classe k viene indicato con $C_{n,k}$ o con il simbolo $$(\table n;k )$$ che prende il nome di coefficiente binomiale e si legge “n su k”.
Costruendo le permutazioni di tutti i sottoinsiemi di k elementi di un insieme I di n elementi (ci sono k! permutazioni per ogni sottoinsieme) si ottengono tutte le disposizioni degli n elementi di I in k posti.
$C_{n,k}·k!=D_{n,k}$
Ne consegue
$$C_{n,k}= D_{n,k}/{k!}=(\table n;k)$$
o anche
$$C_{n,k}={n(n-1)(n-2)..(n-k+1)}/{k!}$$
Moltiplicando numeratore e denominatore della formula precedente per $(n-k)!$ si ha.
$$C_{n,k}={n(n-1)(n-2)..(n-k+1)⋅(n-k)!}/{k!(n-k)!}={n!}/{k!(n-k)!}$$
La combinazione semplice di n elementi di classe k, potrà, allora, essere semplicemente scritta come.
$$C_{n,k}={n!}/{k!(n-k)!}$$
Esempio:
Individuare le combinazioni semplici dei tre oggetti costituenti l’insieme {a,b,c} presi due a due.
Svolgimento:
si tratta di calcolare una combinazione semplice di 3 elementi in classe 2, che possiamo indicare $C_{3,2}$.
Sappiamo già che le disposizioni semplici di classe 2 si calcolano come
$D_{n,k}=n(n-1)(n-2)…(n-k+1)$
in questo caso
$n=3$ con $k=2$ inoltre $(n-k+1)=3-2+1=2$
$D_{2,3}=3·2=6$
e sono le seguenti:
| $ab$ | $ba$ | $ca$ |
| $ac$ | $bc$ | $cb$ |
ora, supponendo che l’ordine non abbia importanza si hanno le identità:
$ab=ba$ ; $ac=ca$ ; $bc=cb$
quindi i raggruppamenti distinti si riducono a
| $ab$ | $\cl"j"{ba}$ | $\cl"j"{ca}$ |
| $ac$ | $bc$ | $\cl"j"{cb}$ |
ossia ${ab,ac,bc}$, conforme alla formula:
$$C_{3,2}=D_{3,2}/{2!}=6/2=3$$
Esempio:
un barista dispone di 30 liquori diversi. Calcolare quanti aperitivi differenti potrà preparare, utilizzando, ogni volta e in parti uguali 3 dei predetti liquori.
Svolgimento:
E’ evidente che l’ordine con cui i 3 diversi liquori vengono mescolati non ha alcuna importanza, quindi il numero di aperitivi differenti che si possono comporre è uguale a quello delle combinazioni semplici dei 30 liquori diversi presi 3 a 3, ossia:
$$C_{30,3}={30·29·28}/{3·2·1}=4060$$
Esempio:
Calcolare il numero di cinquine che si possono formare con i 90 numeri del gioco del Lotto.
Svolgimento:
Nel gioco del Lotto si estraggono cinque numeri da un’urna che contiene i numeri da 1 a 90.
Come si sa, non conta l’ordine con cui i numeri vengono estratti dall’urna; quindi le cinquine che si possono formare con i 90 numeri del gioco del Lotto sono le combinazioni semplici dei numeri 1,2,3,..,90 presi cinque a cinque.
Il numero di cinquine è pertanto:
$$C_{90,5}=D_{90,5}/{5!}={90·89·88·87·86}/{5·4·3·2·1}=43.949.268$$
Esempio:
Calcolare il numeri di cinquine che contengono un terno prefissato nel gioco del Lotto.
Svolgimento:
Le cinquine contenenti un dato terno, ossia tre numeri prefissati, si ottengono aggregando a questa “terna fissa” altri due numeri, scelti in tutti i modi possibili tra i restanti 87.
Di conseguenza le cinquine contenenti un terno prefissato sono tante quante le combinazioni semplici di 87 oggetti presi due a due, cioè:
$$C_{87,2}=D_{87,2}/{2!}=3741$$
Esempio:
Scriviamo le combinazioni semplici dei quattro oggetti appartenenti al seguente insieme:
${1,2,3,4}$
a) presi uno ad uno
b) presi due a due
c) presi tre a tre
d) presi quattro a quattro
Svolgimento:
a) Le combinazioni semplici dei quattro oggetti dati, presi uno ad uno, sono, ovviamente le seguenti:
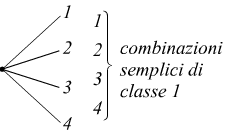
b) Le combinazioni semplici dei quattro elementi dati , presi a due a due, si ottengono dalle precedenti aggregando, uno alla volta, soltanto quegli elementi che, nell'insieme assegnato, seguono l'oggetto già presente nel raggruppamento in esame; ossia
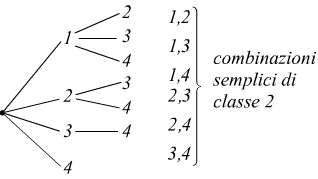
c) Le combinazioni semplici dei quattro oggetti dati, presi tre a tre, si ottengono dalle precedenti di classe due aggregando, uno alla volta, soltanto quegli elementi che nell'insieme assegnato, seguono l'oggetto che figura più a destra ne raggruppamento in esame, ossia:
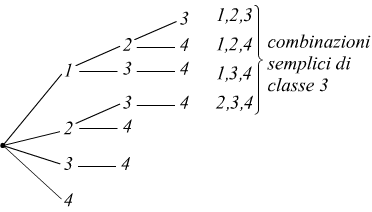
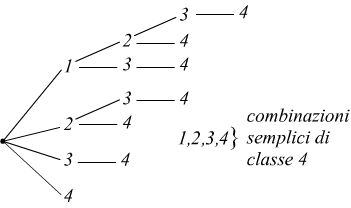
d) Le combinazioni semplici dei quattro oggetti dati, presi quattro a quattro, possono esser derivate dallo schema precedente e sono qui sotto rappresentate:
In questa pagina un calcolatore di calcolo combinatorio online.
Altri argomenti correlati:
Qui sotto un generatore di combinazioni online.
nk
 edutecnica
edutecnica