Disposizioni
Le disposizioni sono tutte le possibili sequenze ordinate di elementi scelti da un insieme.
Le disposizioni si distinguono dalle combinazioni, in quanto le combinazioni non tengono conto dell'ordine degli elementi scelti.
Per ribadire questa distinzione facciamo ancora una volta riferimento all’infografica presentata nella pagina del calcolo combinatorio.
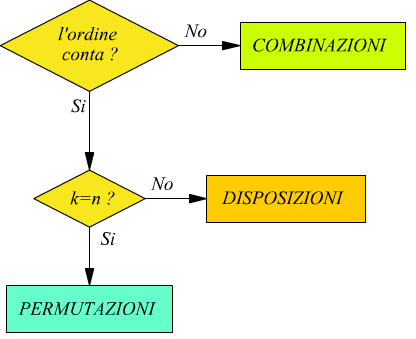
Le disposizioni possono essere semplici oppure con ripetizione.
Per evidenziare questa differenza facciamo un esempio.
Dato l’insieme A={a,b,c,d} scrivere tutte le sigle di due elementi che si possono formare con gli elementi di A.
| aa | ab | ac | ad |
| ba | bb | bc | bd |
| ca | cb | cc | cd |
| da | db | dc | dd |
Questi raggruppamenti sono detti disposizioni con ripetizione di 4 elementi in classe 2 essi sono $4^2=16$.
Classe 2, significa che ogni raggruppamento è costituito da 2 elementi.
Se dall’insieme precedentemente ottenuto escludiamo tutti i raggruppamenti in cui è presente un elemento ripetuto otteniamo il seguente schema:
|
|
ab | ac | ad |
| ba |
|
bc | bd |
| ca | cb |
|
cd |
| da | db | dc |
|
esso è formato da tutti i raggruppamenti formati da 2 elementi diversi; che sono in numero di $4×3=12$. I raggruppamenti di questo tipo vengono detti disposizioni semplici di 4 elementi di classe 2.
Disposizioni semplici
Dopo le precedenti considerazioni possiamo dare la seguente definizione delle disposizioni semplici.
Dati n oggetti distinti, e indicato con k un numero intero positivo minore o uguale a n, si chiamano disposizioni semplici di questi n oggetti, presi a k a k (o di classe k), tutti i raggruppamenti diversi che si possono formare con gli oggetti dati, in modo che valgano le seguenti proprietà:
- ciascun raggruppamento contiene k oggetti;
- uno stesso oggetto non può figurare più volte in un raggruppamento;
- due qualsiasi raggruppamenti sono da considerarsi distinti quando uno di essi contiene almeno un oggetto che non figura nell’altro, oppure gli oggetti di un raggruppamento sono gli stessi dell’altro ma differiscono per l'ordine con cui sono disposti.
Per inquadrare meglio l’argomento facciamo qualche esempio.
Esempio:
Quattro sorelle sono proprietarie di una automobile sportiva a due soli posti.
Sapendo che ciascuna di esse possiede la patente
di guida, vogliamo sapere in quanti modi diversi possono uscire a due a due con quella automobile.
Svolgimento:
L'insieme in esame è composto dalle 4 sorelle che indichiamo con A, B, C, D.
Dobbiamo determinare in quanti modi diversi le 4 sorelle si possono disporre sull'automobile che, come si sa, presenta
solo 2 posti.
Come è facile comprendere, in questo problema l'ordine con cui vengono abbinate le sorelle ha importanza, e inoltre non potranno avvenire ripetizioni.
Evidentemente, alla guida dell'automobile, si può porre a piacere una delle 4 sorelle, con a fianco una qualsiasi delle altre 3.
In base a questa considerazione, i diversi modi con cui le 4 sorelle possono uscire accoppiate in automobile sono descritti dal seguente diagramma ad albero:
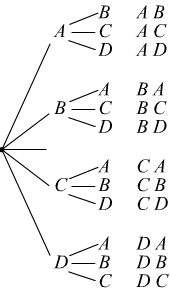
Le coppie ottenute si chiamano disposizioni semplici dei quattro elementi dati, presi a due a due. Il numero di tali disposizioni semplici si indica con $D_{4,2}$ vale:
$D_{4,2} =4·3=12$
Esempio:
Assegnato l’insieme costituito dalle seguenti cinque cifre:
{1,2,3,4,5}
vogliamo sapere quanti siano i numeri di due cifre distinte che si possono scrivere attingendo dall’insieme dato.
Svolgimento:
E’ facile comprendere che, in questo problema, l'ordine con cui vengono prese le due cifre ha rilevanza. La disposizione dei numeri richiesti risulta facilmente deducibile attraverso il seguente diagramma ad albero:
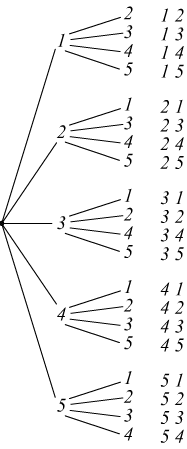
Le coppie ottenute si chiamano disposizioni semplici dei cinque elementi dati, presi a due a due.
Il numero di tali disposizioni semplici si indica con $D_{5,2}$ e vale:
$D_{5,2}=5·4=20$
Esempio:
Dato l’insieme di 4 elementi:
{α, β, γ, δ}
una sua disposizione semplice a 3 a 3 è la terna:
α, β, γ
Un'altra disposizione semplice a 3 a 3 è:
α, δ, γ
che differisce dalla precedente per la presenza di δ al posto di β.
Una nuova disposizione semplice a 3 a 3 è la seguente:
β, α , γ
in quanto differisce da quella iniziale per l’ordine con cui sono disposti gli oggetti.
In generale il numero delle disposizioni semplici degli n oggetti
dati, presi a k a k, si indica con il simbolo: $D_{n,k}$.
Gli esempi precedentemente svolti semplificano la comprensione
della seguente formula, che consente di calcolare il numero delle disposizioni semplici di n oggetti distinti, presi a k a k:
$D_{n,k}=n(n-1)(n-2)·..·(n-k+1)$
Ossia: $D_{n,k}$ è uguale al prodotto di k numeri naturali consecutivi e decrescenti a partire da n.
Avremo allora:
(n=4, k=1) ⟶ $D_{4,1} = 4$
(n=4. k=2) ⟶ $D_{4,2} = 4·3 = 12$
(n=4, k=3) ⟶ $D_{4,3} = 4·3·2 =24$
(n=4, k=4) ⟶ $D_{4,4} = 4·3·2·1 =24$
In questa pagina un calcolatore rapido di disposizioni.
Ci proponiamo, ora di verificare la formula determinando
le disposizioni semplici del primo esempio, costituito dai n=4 elementi
${A, B, C, D}$
presi prima ad uno ad uno, poi a due a due, e cosi via
sino a scrivere quelle a quattro a quattro.
Le disposizioni semplici degli n = 4 oggetti, a uno a uno sono:
$A\;B\;C\;D$
e quindi il loro numero è $D_{4,1} = 4$.
Costruiamo ora le disposizioni semplici dei 4 oggetti dati, a due a due. Esse si ottengono dalle disposizioni semplici di classe uno, gia trovate, aggregando a ciascuna di esse, via via, uno dei tre oggetti che ancora non vi figurano; ossia:

Il numero di disposizioni semplici di classe k = 2, risulta essere:
$D_{4,2}=4·3=12$
Costruiamo ora le disposizioni semplici dei 4 oggetti dati a tre a tre.
Esse si ottengono dalle disposizioni semplici di classe due, già trovate,
aggregando a ognuna di esse, via via, uno dei due elementi che ancora non
vi figurano; cosi facendo, si ha:
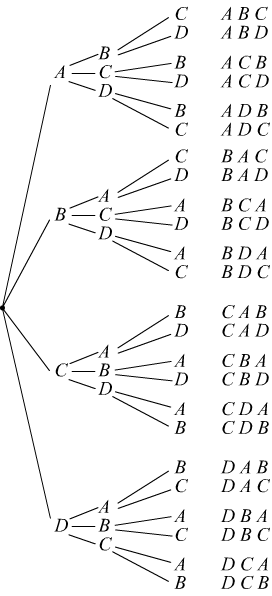
Il numero di tali disposizioni semplici di classe k = 3 risulta:
$D_{4,3} =4·3·2=24$
Infine, per ottenere le disposizioni semplici dei 4 oggetti assegnati, a
quattro a quattro, basta aggregare a ciascuna delle disposizioni semplici
di classe tre l'unico elemento che ancora non vi figura; in tal modo si
ha:
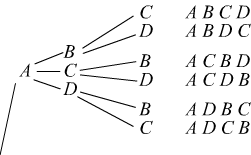
Il numero di tali disposizioni semplici di classe k = 4 risulta:
$D_{4,4}=4·3·2·1=24$
Tutti i risultati trovati in questo esempio sono coerenti con la formula
generale:
$D_{n,k} =n(n-1)(n-2).. (n-k+ 1)$
Altri argomenti correlati:
Qui sotto un calcolatore di disposizioni online
nk
 edutecnica
edutecnica