Disposizioni con ripetizione
Le disposizioni con ripetizione sono un argomento del calcolo combinatorio che si riferisce al numero di modi in cui si possono organizzare gli elementi di un insieme, permettendo la ripetizione di elementi.
In altri termini, in una disposizione con ripetizione, gli elementi possono essere selezionati più volte e possono comparire più volte nella sequenza.
Le disposizioni con ripetizione sono spesso utilizzate nella teoria delle probabilità e nella combinatoria per calcolare il numero di possibili risultati in un esperimento o in una situazione data.
Dopo aver visto in cosa consistono le disposizioni semplici intese come raggruppamenti di n oggetti distinti, presi a k a k. Ci proponiamo ora di introdurre il concetto di disposizioni con ripetizione, così dette perché uno stesso oggetto può figurare ripetuto, anche più volte, all’interno di ciascun raggruppamento.
Nella pagina sulle disposizioni semplici avevamo illustrato il problema attraverso la rappresentazione dell’insieme
$\{a,b,c,d\}$
suddiviso in sigle di due elementi.
| aa | ab | ac | ad |
| ba | bb | bc | bd |
| ca | cb | cc | cd |
| da | db | dc | dd |
QAbbiamo qui evidenziato in rosso la presenza dei gruppi con elementi ripetuti.Dopo aver evidenziato che i raggruppamenti possibili sono $4^2=16$.
Per formare le disposizioni con ripetizione di classe 3 con l’insieme precedente, bisogna associare un elemento dell’insieme {a,b,c,d} a ciascuno dei gruppi precedenti, ottenendo i seguenti raggruppamenti.
| abc | abd |
| acb | acd |
| ... | ... |
| dba | dbc |
| dca | dcb |
In totale si avranno $4^3=64$ gruppi.
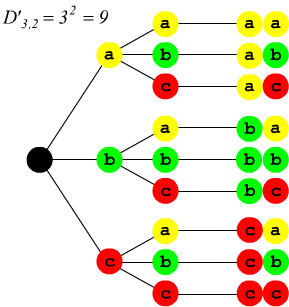
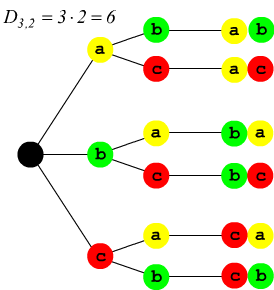
Qui sotto viene messa in evidenza la differenza tra disposizioni semplici e disposizioni con ripetizione di classe due su un insieme di tre elementi $\{a, b, c\}$ utilizzando i diagrammi ad albero.
Disposizione con ripetizione di 3 elementi in classe 2
Disposizione semplici di 3 elementi in classe 2
Facciamo un esempio ancora più facile su un insieme ancor più limitato.
Date le due lettere appartenenti al seguente insieme:
$\{A, B\}$
vogliamo scrivere tutte le disposizioni con ripetizione di
questi oggetti, presi a quattro a quattro.
Utilizziamo un diagramma ad albero, e iniziamo scrivendo le disposizioni con ripetizione delle due lettere A e B, prese ad una ad una; ovviamente si ha:

Indicato con $D'_{2,1}$ il numero di tali disposizioni, evidentemente risulta:
$D'_{2,1}=2$
Per ottenere le disposizioni con ripetizione delle due lettere A e B, prese a due a due, si prolunga ogni ramo del diagramma ad albero precedente, facendo seguire una qualsiasi delle lettere date; così facendo, si ha:

Indicato con $D'_{2,2}$ il numero di tali disposizioni, risulta:
$D'_{2,2}=4$
Per ottenere le disposizioni con ripetizione delle due lettere A e B, prese a tre a tre, si prolunga ulteriormente ogni ramo del diagramma ad albero precedente, facendo ancora seguire una qualsiasi delle lettere date; in tal modo si ha:
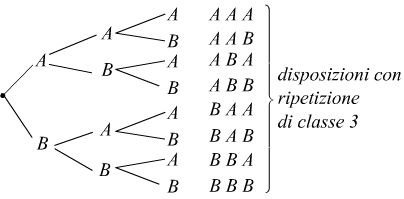
Indicato con $D'_{2,3}$ il numero di tali disposizioni, risulta:
$D'_{2,3}=8$
allo stesso modo possono essere ricavate le disposizioni con
ripetizione delle due lettere A e B, prese a quattro a quattro, e di
verificare che il loro numero risulta:
$D'_{2,4}=16$
In base alle considerazioni precedente è allora possibile dare una definizione di disposizioni con ripetizione.
Dati n oggetti distinti e indicato con k un numero intero positivo qualsiasi (ossia anche maggiore di n), si chiamano disposizioni con ripetizione di questi n oggetti, presi a k a k (o di classe k), tutti i raggruppamenti diversi che si possono formare con gli oggetti dati, in modo che valgano le seguenti proprietà:
- ogni raggruppamento contiene k oggetti;
- in ogni raggruppamento uno stesso oggetto può figurare ripetuto sino a un massimo di k volte;
- due raggruppamenti sono da considerarsi distinti quando uno di essi contiene almeno un oggetto che non figura nellaltro; oppure contengono gli stessi oggetti, ma almeno uno di essi é ripetuto un numero diverso di volte; oppure, pur contenendo gli stessi oggetti, ripetuti lo stesso numero di volte, questi differiscono per l’ordine con cui sono disposti.
Tornando ad un insieme di tre oggetti distinti:
$\{A, B, C\}$
una sua disposizione con ripetizione di classe 4 è la seguente:
A A B B
Un’altra disposizione con ripetizione dei 3 oggetti dati, presi a 4 a 4, è
A A B C
che differisce dalla precedente in quanto contiene l’oggetto C. Una nuova disposizione con ripetizione dei 3 oggetti dati, presi a 4 a 4 è
A A A B
che differisce da quella iniziale, non per gli oggetti, ma per il numero di volte con cui essi sono ripetuti. Infine, la seguente disposizione con ripetizione:
A B A B
differisce da quella iniziale soltanto per l'ordine.
Generalizzando i risultati ottenuti negli esempi svolti, possiamo affermare che il numero delle disposizioni con ripetizione di n oggetti distinti, presi a k a k, è:
$D'_{n,k}=n^k$
Esempio:
Calcolare quanti sono i numeri di cinque cifre, non necessariamente
diverse, che si possono formare con le tre cifre seguenti:
0 1 2
Svolgimento:
Se avessero significato anche i numeri la cui cifra iniziale è zero, allora si potrebbero formare tanti numeri diversi quante sono le disposizioni con ripetizione delle tre cifre date, prese a cinque a cinque, ossia:
$D'_{3,5}= 3^5 = 405$
Ora, da tale risultato occorre detrarre la totalità dei numeri di cinque cifre che sono privi di significato, in quanto iniziano con una o più cifre uguali a zero; ad esempio:
0 1 2 0 1 0 2 0 1 2 0 0 1 2 0 ecc..
La loro quantità è espressa dal numero delle disposizioni con ripetizione delle cifre:
0 1 2
prese a quattro a quattro; ossia:
$D'_{3,4}=3^4=81$
In conclusione, con le tre cifre date si possono formare:
$D'_{3,5}- D'_{3,4}=405-81=324$
numeri diversi di cinque cifre ciascuno.
Altri argomenti correlati:
Qui sotto un calcolatore di disposizioni con ripetizione online
nk
 edutecnica
edutecnica