Permutazioni con ripetizioni
Le permutazioni semplici si riferiscono a disposizioni di elementi senza ripetizione, cioè ogni elemento appare una sola volta in ogni sequenza. E’ possibile considerare permutazioni anche in insiemi dove uno o più elementi si ripetono più volte. Ad esempio nella parola “secchio” la lettere ‘c’ si ripete due volte.
Avremo in tal caso delle permutazioni con ripetizione: esse sono delle disposizioni ordinate degli oggetti di un insieme dove alcuni di questi oggetti sono ripetuti più volte.
A tal proposito ci proponiamo di anagrammare una parola contenente alcune lettere uguali e, per fissare le idee, consideriamo la parola ALA, che contiene due lettere identiche su un totale di tre.
I possibili anagrammi distinti sono i seguenti:
A L A A A L L A A
Come si può vedere, il numero di tali anagrammi è 3, e non 6, come accade nei casi in cui le lettere sono tutte diverse. Ciò è dovuto al fatto che, scambiando tra loro le lettere identiche di una parola, ossia permutandole, quella parola rimane invariata. Infatti, si ha:
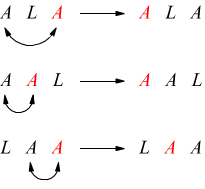
Indicato con $P^2_3$ il numero degli anagrammi distinti della parola ALA, costituita di tre lettere, due delle quali sono identiche, si ha:
$P^2_3=3$
Se le tre lettere si supponessero diverse, allora il numero degli anagrammi sarebbe:
$P_3=3!=6$
Essendo 2! il numero di permutazioni delle due lettere identiche ad A, si nota che tra $P^2_3$ e $P_3$ sussiste la seguente relazione:
$P^2_3⋅2!=P_3$
e quindi si può scrivere
$$P^2_3=P_3/{2!}=6/2=3$$
Più in generale, $P^2_3$ indica il numero delle permutazioni di tre oggetti, due dei quali sono identici.
Consideriamo un secondo esempio piuttosto sintomatico.
Consideriamo i sei oggetti seguenti:
A A B T T T
ove l'oggetto A è ripetuto due volte e l'altro oggetto, T, è ripetuto tre volte. Vogliamo calcolare il numero delle permutazioni con ripetizione che si possono formare con gli oggetti dati; tale numero si indica con il simbolo:
$P^{2,3}_6$
Se i sei oggetti fossero tutti diversi allora il numero delle permutazioni (semplici) risulterebbe:
$P_6=6!=720$
Sapendo, però, che due degli oggetti dati sono identici ad A, allora le loro $2! = 2$ permutazioni non hanno provocato alcun cambiamento all’interno dei vari raggruppamenti; di conseguenza il numero delle permutazioni distinte dei 6 oggetti dati si riduce a:
$$P_6/{2!}=720/2=360$$
Sapendo poi che tre degli oggetti assegnati sono identici a T, allora anche le loro $3! = 6$ permutazioni non hanno prodotto alcun cambiamento all’interno dei vari raggruppamenti; quindi il numero delle permutazioni distinte dei 6 oggetti dati si riduce ulteriormente a:
$$P^{2,3}_6=P_6/{2!⋅3!}=720/12=60$$
In generale, se si hanno n oggetti, uno dei quali figura ripetuto $α$ volte (mentre i rimanenti $n-α$ sono diversi), il numero delle permutazioni distinte degli n oggetti dati risulta:
$$P^α_n={n!}/{α!}$$
Se tra gli n oggetti dati, ne esistono $α$ identici, e altri $β$ uguali tra loro, allora il numero delle permutazioni distinte degli n oggetti assegnati risulta:
$$P^{α,β}_n={n!}/{α!β!}$$
Analogamente si procede se anche altri oggetti sono identici.
Per fare un ulteriore esempio in merito a quest'ultima eventualità, calcoliamo il numero degli anagrammi che si possono scrivere con la parola MATEMATICA.
Gli oggetti dati sono le n = 10 lettere della parola MATEMATICA. Tra di esse figurano le seguenti ripetizioni:

Di conseguenza, il numero degli anagrammi richiesto è:
$$P^{3,2,2}_10={10!}/{ {3!} {2!} {2!}}=151.200$$
e ancora:
quanti numeri naturali diversi di sei cifre ciascuno si possono formare
con le cifre del numero 775551?
In questo caso, i numeri che si vogliono scrivere sono le permutazioni con ripetizione delle n = 6 cifre del numero dato. Tra di esse figurano le seguenti ripetizioni:

Di conseguenza, permutando in tutti i modi possibili le cifre del numero dato, si possono scrivere:
$$P^{2,3}_6={6!}/{2!⋅3!}=60$$
numeri naturali diversi.
Altri argomenti correlati:
 edutecnica
edutecnica