Calcolo combinatorio
Il calcolo combinatorio è quel settore della matematica che ha come oggetto il calcolo dei modi con i quali possono essere raggruppati e ordinati, secondo date regole, gli elementi di un insieme finito.
La maggior parte dei problemi di calcolo combinatorio sono riconducibili al seguente quesito: quanti raggruppamenti di $k$ elementi si possono costruire con un insieme di $n$ (considerando $k≤n$ ) elementi distinti?
Per procedere nella soluzione del problema, dobbiamo specificare alcune cose ulteriori:
- è importante l'ordine degli elementi nei raggruppamenti ?
- Sono consentite delle ripetizioni di elementi ?
Una volta individuate le caratteristiche in merito all'ordine e alle possibilità di ripetizione, non resta che eseguire il tipo di calcolo appropriato, che si diversifica in funzione delle condizioni specificate.
Consideriamo per semplicità l'insieme costituito dalle lettere dell'alfabeto dalla A alla Z.
A, B, C,.., Z
e supponiamo di voler costituire dei raggruppamenti (sottoinsiemi) con questi simboli; diciamo raggruppamenti di 3 elementi.
E' ovvio che questi raggruppamenti si possono ottenere in modi diversi, come si vede nei seguenti casi:
ABC, BCA, ACD, AAB
Come si vede, i primi due differiscono solo per l'ordine secondo il quale sono stati presi; il primo e il terzo differiscono per un elemento; nel quarto l'elemento A viene ripetuto due volte.
Quelli che seguono sono dei tipici problemi di calcolo combinatorio che richiedono una valutazione preventiva delle condizioni menzionate.
| Quante parole di 4 lettere tutte diverse si possono formare con le 21 lettere dell'alfabeto italiano? | I diversi modi in cui si possono succedere le 4 lette dipendono dall'ordine in cui vengono scelte; inoltre non possono esserci ripetizioni perchè esse devono essere tutte diverse. | Raggruppamenti ordinati SENZA ripetizioni. |
| In quanti modi si possono presentare le facce di due dadi | Se il lancio restituisce un accoppiamento 3,4 questo deve essere considerato diverso dall'accoppiamento 4,3; in questo caso l'ordine conta. Inoltre sono ammesse ripetizioni del tipo 2,2. | Raggruppamenti ordinati CON ripetizioni. |
| Quanti ambi si possono formare con i 90 numeri del lotto? | Nel gioco lotto al fine della vincita hanno importanza solo i numeri estratti, non l'ordine di estrazione. Nel conteggio degli ambi non ha importanza l'ordine dei numeri; inoltre non ci possono essere ripetizioni, perchè le estrazioni sono senza reimmissione. | Raggruppamenti NON ordinati SENZA ripetizioni. |
| Con i tre colori verde, rosso e blu (RGB)quanti altri colori si possono ottenere? | Ammettendo la possibilità di ripetere eventualmente uno o più colori? In questo caso l'ordine non conta perché si potrebbe scegliere RGB o anche BGR, inoltre sono ammesse ripetizioni come RRB o GGB etc.. | Raggruppamenti NON ordinati CON ripetizioni. |
Queste ed altre osservazioni mettono in evidenza il fatto che i raggruppamenti possono essere costruiti seguendo leggi diverse. Dunque, il calcolo combinatorio studia ed insegna a contare i diversi raggruppamenti che si possono ottenere da un insieme di oggetti dati prendendo ogni volta un certo numero di essi. In generale si fa distinzione tra :
- raggruppamenti senza ripetizioni detti raggruppamenti semplici
- raggruppamenti con ripetizioni
Precisamente
- semplici sono quelli nella cui costruzione non è prevista la possibilità che, all'interno di uno stesso raggruppamento, uno stesso oggetto venga ripetuto;
- con ripetizione sono quelli nella cui costruzione è prevista la possibilità che , all'interno di uno stesso raggruppamento, uno stesso elemento venga ripetuto.
Riassumendo, secondo talune regole, è importante l’ordine dei gruppi formati; in questo caso i raggruppamenti si chiamano disposizioni.
Nel caso specifico che sia n=k (cioè numero degli elementi di ogni gruppo pari al numero di elementi dell’insieme di origine) si chiamano permutazioni.
Secondo altre regole, l’ordine degli elementi non ha importanza e, in tal caso, i raggruppamenti si chiamano combinazioni.
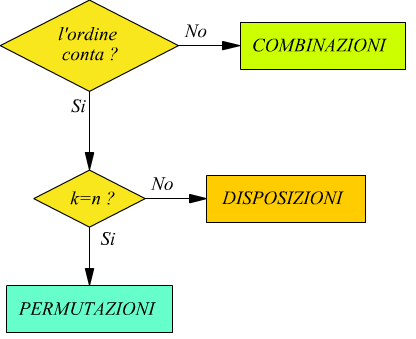
In certi casi i gruppi conterranno elementi diversi l'uno dall'altro e pertanto si parla di disposizioni semplici, permutazioni semplici e combinazioni semplici. In altri casi i raggruppamenti conterranno oggetti che vi figurano una o più volte, in tale eventualità si parla di disposizioni con ripetizione, permutazioni con ripetizione, combinazioni con ripetizione.
In generale si considera un insieme :
$I=\{a_1, a_2, .., a_n\}$
costituito da n elementi , di natura qualunque, ma perfettamente distinguibili l’uno dall’altro, in base a qualche caratteristica. Ad esempio: palline di colore diverso, lettere dell’alfabeto, cifre diverse ecc..
Il calcolo combinatorio ha per scopo la costruzione e la misurazione del numero di raggruppamenti distinti che, secondo una assegnata definizione, si possono formare con una certa quantità degli elementi dell’insieme.
I possibili raggruppamenti sono allora i seguenti:
- disposizioni semplici
- disposizioni con ripetizione
- permutazioni semplici
- permutazioni con ripetizione
- combinazioni semplici
- combinazioni con ripetizione
Principio fondamentale del calcolo combinatorio
Supponiamo di aver a disposizione due paia di pantaloni e di tre camicie. In quanti modi diversi ci possiamo vestire?
Chiamiamo P l’insieme rappresentativo dei pantaloni con
$P=\{p_1, p_2\}$
Chiamiamo C l’insieme rappresentativo delle camicie con
$C=\{c_1, c_2, c_3\}$
Elenchiamo i possibili accoppiamenti che non sono altro che il prodotto cartesiano tra i due insiemi:
$P×C=\{(p_1;c_1), (p_1;c_2), (p_1;c_3), (p_2;c_1), (p_2;c_2), (p_2;c_3)\}$
Il diagramma ad albero seguente suggerisce il metodo per trovare tutti i gruppi che si possono formare.
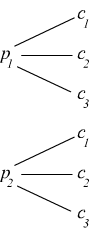
Le 2 eventualità corrispondenti ai rami dei pantaloni indicano quante volte vengono ripetute le tre eventualità corrispondenti ai rami delle camicie.
Quindi in totale abbiamo $2×3=6$ gruppi.
Supponendo di non voler rinunciare ad un minimo di eleganza, e di voler associare a questi 6 abbinamenti un ulteriore elemento come una delle due giacche dell’insieme:
$G=\{g_1,g_2\}$
Il diagramma seguente permette di visualizzare il numero complessivo di abbinamenti fra giacche G, pantaloni P e camicie C.
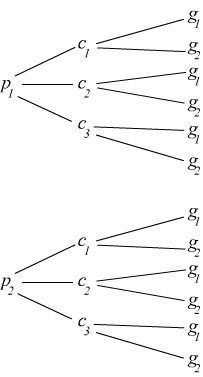
Osservando la disposizione del grafico notiamo come stavolta possono essere assemblati un numero superiore di raggruppamenti dati da
$2×3×2=12$
eventualità.
Possiamo a questo punto enunciare il principio fondamentale del calcolo combinatorio.
Se un oggetto è univocamente individuato da una sequenza di n scelte tali che vi siano $k_1$ possibilità per la prima scelta, $k_2$ per la seconda scelta e $k_n$ per l’n-esima scelta, il numero totale di raggruppamenti che si possono formare è dato dal prodotto $k_1·k_2·…·k_n$
Altri argomenti correlati:
 edutecnica
edutecnica