Combinazioni con ripetizione
Ci proponiamo ora di introdurre il concetto di combinazioni con ripetizione, così dette perché uno stesso elemento può figurare ripetuto, anche più volte, all’interno di ciascun raggruppamento. Anche nella formazione delle combinazioni con ripetizione non conta l’ordine degli oggetti.
Dati n elementi distinti e indicato con k un numero intero positivo qualsiasi (ossia anche maggiore di n), si chiamano combinazioni con ripetizione di questi n elementi presi a gruppi di k (o di classe k) tutti i raggruppamenti diversi che si possono formare con gli elementi dati, in modo che valgano le seguenti proprietà:
ogni raggruppamento contiene k elementi;
in ogni raggruppamento uno stesso elemento può figurare ripetuto fino ad un massimo di k volte;
l’ordine degli elementi non conta, e quindi due raggruppamenti sono da considerarsi diversi quando uno di essi contiene almeno un elemento che non figura nell’altro, oppure contengono gli stessi elementi ma non ripetuti lo stesso numero di volte.
Possiamo notare che essendo ammesso ripetere gli oggetti può essere $k≥n$; si può, allora, dimostrare il seguente teorema:
Il numero di combinazioni con ripetizione di $n$ oggetti di classe $k$, che indichiamo con $C'_{n,k}$ equivale al numero di n-uple di interi non negativi $(x_1,.., x_n)$ soluzioni dell’equazione $x_1+x_2+..+ x_n=k$ ed è assegnato dalla formula:
$$C’_{n,k}=(\table {n+k-1};k )={(n+k-1) (n+k-2)..(n+1)n}/{k!}$$
Esempio:
dati due oggetti appartenenti allo stesso insieme {A,B} vogliamo scrivere tutte le combinazioni con ripetizione di questi oggetti presi tre a tre svolgimento: utilizzando un diagramma ad albero si ha:
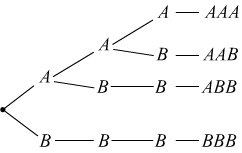
Come si può vedere ciascuna di tali combinazioni con ripetizione dei due oggetti assegnati, contiene tre elementi, ed uno stesso elemento può figurare ripetuto sino ad un massimo di tre volte. Le due combinazioni con ripetizione
AAA e BBB
sono distinte, perché contengono elementi differenti.
Sono altrettanto distinte le due seguenti combinazioni con ripetizione
AAB e ABB
perché pur contenendo gli stessi oggetti , sono diversamente ripetuti.
Sono invece identici i due raggruppamenti seguenti:
AAB e ABA
in quanto differiscono solo per l'ordine, caratteristica che non conta trattandosi di combinazioni.
Indicato con $C'_{2,3}$ il numero delle combinazioni con ripetizione dei due oggetti distinti presi tre a tre, si è trovato che $C'_{2,3}=4$; infatti applicando la formula
$$C'_{n,k}=(\table {n+k-1};k )={(n+k-1) (n+k-2)..(n+1)n}/{k!}$$
con n=2 e k=3 si ha n+k-1=2+3-1=4 e quindi
$$C'_{2,3}=(\table 4;3 )={4⋅3⋅2}/{3!}=4$$
Esempio:
applicando la formula, calcoliamo il numero di combinazioni con ripetizione dei tre oggetti
{a,b,c}
presi tre a tre. Poi ci proponiamo di determinare nuovamente questo numero, procedendo per via diretta , ossia scrivendo effettivamente tutte le combinazioni dei 3 oggetti dati, di classe 3.
Svolgimento:
In questo caso è n=3 e k=3
perciò
n+k-1=3+3-1=5
dunque
$$C'_{3,3}=(\table 5;3 )={5⋅4⋅3}/{3!}=10$$
Ora, usando un diagramma ad albero, scriviamo effettivamente le combinazioni
con ripetizione dei tre oggetti dati, prima presi uno ad uno, poi due a
due ed infine tre a tre.
Cosi facendo si ha:
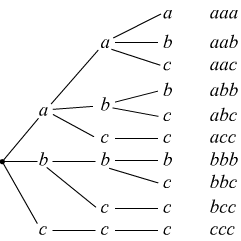
Come si può vedere , contando le diverse combinazioni ottenute, si ritrova che: $C'_{3,3}=10$.
Esempio:
Calcoliamo il numero di modi diversi con cui sette cioccolatini uguali, possono essere distribuiti a tre bambini.
Svolgimento:
Indichiamo con le lettere:
A B C
i tre bambini a cui si vogliono distribuire i sette cioccolatini. Consideriamo una qualsiasi combinazione con ripetizione di A, B, C di classe sette; per fissare le idee, la seguente: ;
A A B B B B C
con essa intendiamo dire che il bambino A riceve 2 cioccolatini, B ne riceve 4 e, infine, il bambino C ne riceve 1 solo. Con quest’altra combinazione con ripetizione di classe sette:
A A A A A B B
intendiamo dire che il bambino A riceve 5 cioccolatini, B ne riceve 2, mentre C, purtroppo, non ne riceve alcuno.
Da queste considerazioni si comprende che le diverse modalità di distribuzione dei sette cioccolatini ai tre bambini sono tante quante le combinazioni con ripetizione di n = 3 elementi di classe k = 7, e cioè:
$$C'_{3,7}=(\table {7+3-1};7 )=(\table 9;7 )={9⋅8\cl"j"{⋅7⋅6⋅5⋅4⋅3}}/{\cl"j"{7⋅6⋅5⋅4⋅3⋅}2⋅1}=36$$
Bisogna osservare, in generale, che i problemi riguardanti le modalità di distribuzione in gruppi di oggetti indistinguibili, ossia per i quali non si opera distinzione tra gli oggetti stessi (come i cioccolatini dell’esempio precedente) si risolvono mediante le combinazioni con ripetizione.
Esempio:
Calcolare le differenti modalità con cui sei penne identiche possono essere riposte in quattro cassetti A, B, C, D. Supponendo, invece, che le penne siano distinguibili, quante diventano tali modalità ?
Svolgimento:
Poiché le 6 penne sono tutte uguali, ossia indistinguibili l'una dall’altra, allora le differenti modalità con cui esse possono essere collocate nei 4 cassetti sono tante quante le combinazioni con ripetizione di n = 4 oggetti di classe k = 6, ossia:
$$C'_{4,6}=(\table {4+6-1};6 )=(\table 9;6 )={9⋅8⋅7⋅\cl"j"{6⋅5⋅4}}/{\cl"j"{6⋅5⋅4}⋅3⋅2⋅1}=84$$
Se invece le penne sono distinguibili l'una dall’altra, ad esempio perché di colore diverso:
bianco, nero, rosso, verde, giallo, blu
allora il numero dei modi con cui queste penne possono essere collocate nei quattro cassetti sarebbe maggiore. Per convincersi di ciò, basti pensare che, ad esempio, la seguente situazione:

mentre si realizza secondo un'unica modalità, nel caso in cui le penne siano indistinguibili, si può invece ottenere mediante sei modalità differenti, nell'eventualità in cui le penne siano colorate, e cioè una distinta modalità per ogni colore della penna riposta nel cassetto A.
Dunque, questa volta, l'ordine ha importanza quindi occorre utilizzare le disposizioni.
Dopo queste constatazioni, vediamo come può essere interpretata una qualsiasi disposizione con ripetizione dei 4 cassetti A, B, C, D di classe 6; ad esempio, la seguente disposizione con ripetizione:
A A B B B C
può essere cosi interpretata:
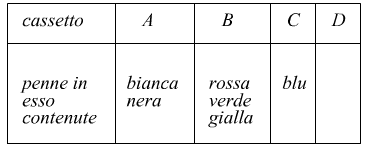
Consideriamo ora un'altra disposizione con ripetizione di A, B, C, D di classe 6:
B A C C C D
può essere cosi interpretata:
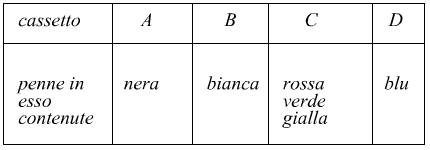
Procedendo su questa via, si comprende che le differenti modalità con cui le sei penne distinguibili (perché di diverso colore) possono essere collocate in quattro cassetti sono tante quante le disposizioni con ripetizione di n = 4 oggetti di classe k = 6, ossia:
$D'_{4,6}=4^6=4096$
Altri argomenti correlati:
Qui sotto un volgare generatore di combinazioni con ripetizione online.
nk
 edutecnica
edutecnica