La forza
Per definizione, la forza è un fenomeno fisico che provoca cambiamenti del moto di un oggetto oppure provoca la deformazione di un oggetto.
La forza può cambiare la velocità di un corpo.
- Se il corpo continua a rimanere fermo, allora la forza totale che è applicata su di esso è uguale a zero.
- Se invece comincia a muoversi, allora è applicata una forza totale diversa da zero che modifica la sua velocità.
Una variazione di velocità di un oggetto corrisponde alla presenza di una accelerazione. Dunque, forza ed accelerazione sono due grandezze fisiche strettamente correlate.

Misura della forza
Possiamo basarci anche solo su una nozione intuitiva di forza, derivata dalla nostra esperienza quotidiana, come quella della forza necessaria per sollevare o spingere un peso. Questa nozione intuitiva suggerisce che la forza è una quantità vettoriale.
Per descrivere una forza occorrono tre informazioni.
- La sua direzione, cioè la retta lungo cui la forza agisce.
- Il verso in cui è orientata dato che su una singola direzione ci sono due versi possibili.
- La sua intensità ( o modulo ) che può essere misurata con un dinamometro.
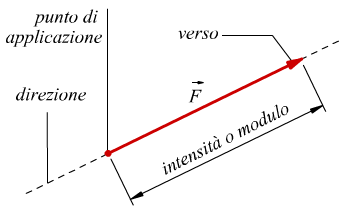
Il punto di applicazione di una forza, che indica il punto specifico in cui la forza viene applicata su un oggetto, rappresenta un’informazione supplementare di non secondaria importanza.
L'unità di misura della forza è il newton che ha simbolo N.
Per definizione un newton è pari all'intensità della forza peso con cui la terra attrae un corpo di massa uguale a 102 grammi.
Alternativamente possiamo dire che la terra esercita una forza di 9,8N su un oggetto di massa 1kg a livello del mare.
Tipi di forze
Le principali tipologie di forze possono suddivise in due categorie:
- Forze di contatto.
- Forze a distanza.
Tra le forze di contatto possiamo annoverare le seguenti:
- Forza di attrito : forza che si oppone al movimento di un oggetto quando scorre o rotola su una superficie (di contatto).
- Forza elastica : forza esercitata da un materiale elastico quando viene compresso o allungato (di contatto).
- Forza di tensione : forza esercitata da un corpo quando viene teso o allungato da due punti di ancoraggio, come nel caso di una fune.
Tra le forze di a distanza possiamo abbiamo:
- Forza di gravità : forza attrattiva esercitata da un corpo su un altro dovuta alla massa dei corpi e alla distanza tra di essi (a distanza).
- Forza magnetica : forza che agisce tra materiali magnetizzati o tra magneti e materiali ferrosi (a distanza).
- Forza elettrostatica : forza che agisce tra cariche elettriche, positiva e negativa (a distanza).
- Forza nucleare : forza che tiene insieme protoni e neutroni all'interno del nucleo atomico.
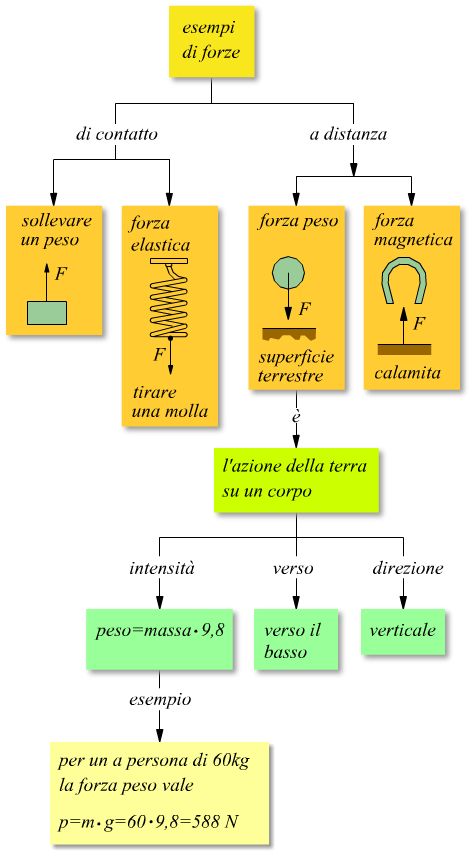
Classificazione delle forze
Nel contesto della meccanica classica (newtoniana) dobbiamo esclusivamente considerare solo le forze di contatto e la forza di gravità (forza a distanza) che determina la forza peso. In questo caso le forze che si manifestano possono essere classificate in due categorie principali.
- Forze attive.
- Forze reattive.
Le forze attive sono le forze agenti sul sistema che non sono dovute ai vincoli; esse si dividono in:
- Forze interne: sono quelle forze agenti sul sistema provenienti da altri punti interni al sistema stesso. Sono le forze molecolari fra le molecole del sistema, quelle dovute alle contrazioni muscolari in un essere animato, quelle originate dal motore di un automobile.
- Forze esterne: sono le forze agenti sul sistema dovute all'azione di punti esterni al sistema., come le forze peso, le forze esercitate mediante fili esterni al sistema, le resistenze aerodinamiche, etc..
- Forze motrici: sono quelle forze agenti sul sistema, siano esse interne od esterne che favoriscono il moto, cioè forniscono energia al sistema. Queste forze sono dovute a motori o a forze peso.
- Forze resistenti: sono quelle forze agenti sul sistema, siano esse interne od esterne. che si oppongono al moto, cioè sottraggono energia al sistema. Tipiche sono le resistenze aerodinamiche, le forze dovute alla viscosità o agli attriti.
Le forze reattive o reazioni vincolari sono quelle forze che immaginiamo di sostituire ai vincoli per mantenere la stessa configurazione di equilibrio (in statica) o lo stesso movimento (in dinamica).
Quindi le forze possono essere classificate nel seguente modo
$\{\table forze\;\;attive\;\;interne ; forze\;\;attive\;\;esterne $
$\{\table forze\;\;reattive\;\;interne ; forze\;\;reattive\;\;esterne $
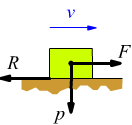
Ad esempio se il sistema è un'automobile:

A : forza attiva esterna (resistente).
R : forze reattive esterne.
P : peso, forza attiva esterna (motrice in discesa,
resistente in salita).
K : attrito, forza reattiva esterna.
F : forza motrice, forza attiva interna che è la
forza generata durante lo scoppio sul pistone nella camera di combustione.
Operazioni sulle forze
La forza è dunque un vettore, dotato di intensità, o modulo, direzione
e verso. Ciò significa che quando due o più forze agiscono su un corpo,
possiamo comporle per trovare la forza netta o forza risultante, semplicemente
operando l'addizione vettoriale delle singole forze secondo le regole assegnate
nella pagina sui vettori.
Una sola forza dunque, che presenti il modulo, la direzione e il verso della
risultante di questa somma, produce sul corpo lo stesso effetto che verrebbe
prodotto da tutte le forze componenti agenti insieme su di esso.
Questa proprietà è detta principio di sovrapposizione delle forze. Nello
schema seguente si riassumono queste proprietà.

Quando le forze si trovano su diverse rette di azioni si parla di forze concorrenti. Per trovare la forza risultante netta F, in questo caso, oltre al metodo grafico del parallelogramma è possibile usare la formula del teorema di Carnot.
$$F=√{F_1^2+F_2^2+2·F_1·F_2·cosα}$$
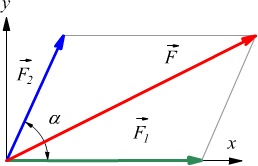
con α angolo formato tra le due forze $F_1$ ed $F_2$ di cui deve essere nota l’intensità.
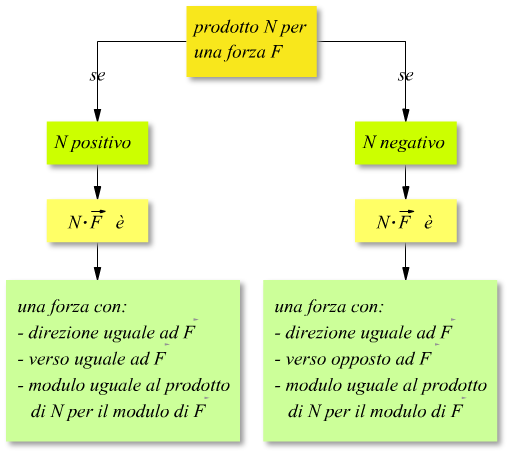
Rimane invariata anche la proprietà della moltiplicazione (o divisione) di una forza per un valore scalare.
Di particolare importanza rimane la tecnica della scomposizione di un vettore nelle sue componenti cartesiane x ed y .

Nello schema successivo viene messo in evidenza come sia possibile trovare la forza netta F risultante dalla somma di due vettori $F_1$ ed $F_2$ sia col metodo grafico punta-coda che attraverso la somma cartesiana dei due vettori componenti.
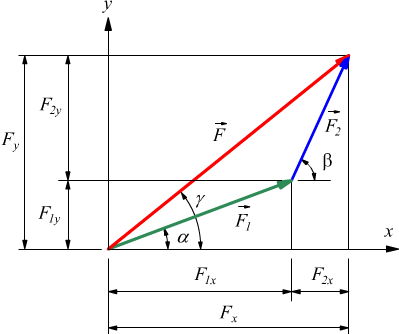
I due vettori $F_1$ e $F_2$ si possono sommare geometricamente disegnandoli nella medesima scala e collocandoli uno di seguito all'altro, cioè ponendo la coda del secondo in corrispondenza della punta del primo. Il vettore che congiunge la coda di $F_1$ alla punta di $F_2$ è il vettore somma F.
In alternativa possiamo usare il metodo analitico delle componenti cartesiane, considerando che:
$\{\table F_{1x}=F_1cosα ; F_{1y}=F_1sinα $
$\{\table F_{2x}=F_2cosβ ; F_{2y}=F_2sinβ $
$\{\table F_x=F_{1x}+F_{2x} ; F_y=F_{1y}+F_{2y} $
$\{\table F=√{F_x^2+F_y^2} ; γ=arctg(F_y/F_x) $
Forza-peso
Sulla terra tutti gli oggetti hanno un peso, ma prima di parlare di "peso" è meglio chiarire un frequente malinteso. Quando noi cerchiamo di capire quanto pesiamo, semplicemente saliamo su una bilancia, ma il valore che leggiamo, in kg, non è il nostro peso, bensì la nostra massa (infatti la massa si misura in kg). A questa massa è associata una forza peso data dalla formula:
$p↖{→}=m·g↖{→}$
p è dunque la nostra forza-peso e si misura in newton [N] mentre $g=9,81m/{s^2}$ è l’accelerazione di gravità. La forza peso è un vettore con intensità p, diretta verticalmente con senso verso il basso con punto di applicazione, idealmente, fissato nel baricentro dell’oggetto in qustione. La formula è diretta conseguenza della seconda legge di Newton $F↖{→}==m·a↖{→}$ e con la definizione di forza data all’inizio.
Forza di attrito
Le forze di attrito sono forze di contatto passive che si incontrano frequentemente in numerosi problemi di fisica. Ciò è dovuto al fatto che i corpi non sono liberi nello spazio ma si muovono sempre a contatto con altri corpi o in mezzo ad un fluido. Dato che le superfici a contatto non sono mai perfettamente lisce e c’è sempre la presenza di aria, nascono delle resistenze che si oppongono al moto. Per questo motivo non sarà mai possibile che un corpo si muova eternamente per inerzia, ma ben presto rallenterà e si fermerà per effetto delle resistenze passive di attrito.
In prima battuta le resistenze di attrito possono essere classificate come:
- Resistenza di attrito, per effetto del contatto tra corpi in movimento. L’attrito di strisciamento viene chiamato attrito radente, l’attrito di rotolamento viene chiamato attrito volvente.
- Resistenza del mezzo, per effetto della presenza di un fluido durante il moto, come può essere l’aria o l’acqua.
Si ha attrito radente quando un corpo striscia su un altro. La resistenza di attrito R che nasce dallo strisciamento è diretta in senso opposto a quella del movimento ed è causata dall’inevitabile rugosità delle superfici a contatto.
L’attrito dipende dalla natura dei corpi a contatto e dal grado di rugosità
delle loro superfici.
L’attrito è direttamente proporzionale alla pressione normale che il corpo
in moto esercita sulla superficie di contatto.
L’attrito di primo distacco è generalmente 1,5÷3 volte maggiore di
quello durante il moto .
Si chiama coefficiente di attrito ($f$) il rapporto tra la resistenza di attrito R (in newton [N]) e la pressione normale p (in N) al piano di strisciamento o di rotolamento.
$$f=R/p$$
La resistenza di attrito $f$ può essere, dunque, ottenuta dalla formula:
$R=f·p$
Nella tabella seguente sono riportati i valori medi di alcuni coefficienti di attrito.
| superfici | secche | lubrificate |
| Acciaio su acciaio | 0,2 | 0,1 |
| Ghisa su ghisa | 0,12 | 0,07 |
| Bronzo su ghisa | 0,15 | 0,08 |
| Cuoio su ghisa | 0,5 | - |
| Metallo su legno | 0,5 | 0,2 |
| Legno su legno | 0,4 | 0,15 |
Dinamometro
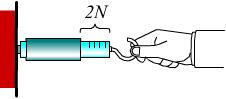
La misura di una forza può essere effettuata tramite il dinamometro. Lo strumento è costituito da una molla inserita in un involucro cilindrico che ha una parte fissa ed una mobile.

Sulla parte mobile è riportata una scala graduata che permette di misurare
l’allungamento della molla.
Lo zero della scala corrisponde all’assenza della forza applicata.
Quando alla molla viene applicata una forza, la parte mobile fuoriesce ed
è possibile valutare l’intensità della forza sulla scala graduata.
La semplicità di questa misura è dovuta alla legge fisica che la sottende:
la legge di Hooke che mette in relazione l’allungamento x della molla con
la forza di richiamo F.
$F=-k·x$
Noto il valore della costante elastica k della molla e dell’allungamento x della stessa è possibile trovare la forza F applicata.
Argomenti correlati :
 edutecnica
edutecnica