Dinamica
Mentre la statica si interessa l'equilibrio dei corpi rigidi soggetti a sistemi di forze, la cinematica si occupa del moto del movimento di tali corpi, la Dinamica studia il moto dei corpi in relazione alle cause che lo producono o ne cambiano le caratteristiche
Questo argomento della meccanica può essere suddiviso in due parti:
•dinamica del moto traslatorio
•dinamica del moto rotatorio
La differenza tra questi due tipi di moti è piuttosto evidente, basti pensare al tipo di spostamento compiuto attraverso questi due atti di moto e alla definizione di velocità nei due casi di moto rettilineo uniforme (traslatorio) e circolare uniforme (rotatorio) per un punto materiale
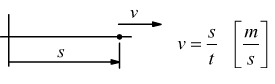

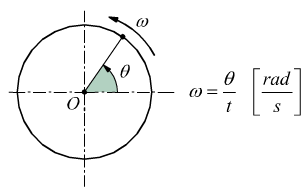

Come si vede il moto traslatorio ricade nel primo caso: si ha uno spostamento lineare in una direzione e la velocità viene espressa come lo spazio percorso nell'unità di tempo: m/s . Nel caso del moto rotatorio lo spazio misurato è un angolo (θ) che generalmente viene espresso in radianti, in tal modo si definisce la velocità del moto rotatorio, come la quantità di gradi (radianti) percorsi sull'unità di tempo (sec.) la velocità è misurata appunto in rad/sec.
Leggi della Dinamica
Lo studio del moto di traslatorio si basa sulle tre leggi fondamentali della dinamica, anche chiamate leggi di Newton.
Ia legge della Dinamica (o legge d'inerzia).
Un corpo rimane nel suo stato di quiete o di moto rettilineo uniforme
fino a che non interviene una forza esterna in grado di alterare quello
stato.
IIa legge della Dinamica.
Una forza applicata a un corpo gli imprime una accelerazione proporzionale
all' intensità della forza stessa e orientata nella stessa direzione.
Si parla in questo caso di una forza non equilibrata da altre, oppure,
della risultante di tutte le forze agenti sul corpo.
Se il corpo rigido si trova su un piano su quale può muoversi senza
attrito (trascurando anche l'attrito della viscosità dell'aria, quindi
nel vuoto) si esprime la IIa legge come
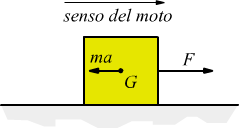
![]()
Il termine m·a è chiamato forza di
inerzia.
(F) è la forza applicata, mentre (a) è l'accelerazione acquisita dal
corpo, con (G) indichiamo il baricentro del corpo . (a) ed (F) sono
dunque vettori fra loro proporzionali, mentre con m si indica una costante
di proporzionalità.
Se oltre ad (F) vi è un'altra forza resistente (R) (ad es. dovuta all'attrito)
si scriverà :
![]()
La somma al primo membro deve essere intesa come somma algebrica. Se per semplicità F ed R si trovano sulla stessa retta di azione con verso opposto come indicato nel disegno, bisognerà sottrarre R (negativa nel senso x) ad F (positiva nel senso x) per ottenere la forza risultante da riportare al primo membro.
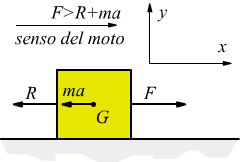
in altri termini notando che sia (F) che (R) che l'eventuale accelerazione (a) saranno dotate della stessa direzione (lungo l'asse x orizzontale) si scriverà
![]()
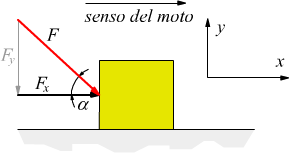
Se F>R il corpo tenderà a spostarsi nel senso positivo dell'asse x e il vettore m·a si opporrà alla realizzazione di questo movimento ; sarà dunque diretto nel senso negativo dell'asse x.
Se F<R il corpo tenderà a fermarsi decelerando e il vettore m·a
si opporrà a questa eventualità e sarà orientato nel senso positivo delle
x.
In sintesi la direzione dei vettori sarà la seguente:
Modus operandi
Quando cerchiamo di risolvere un problema di dinamica del corpo rigido, dobbiamo prima di tutto farci un'idea del tipo di moto con cui abbiamo a che fare:
● La direzione del moto coincide con il vettore velocità.
● Se il moto è accelerato, il vettore accelerazione e il vettore velocità hanno lo stesso verso.
● Se il moto è ritardato (decelerato) il vettore accelerazione ha verso contrario al vettore velocità
● Il vettore forza di inerzia (m·a) si oppone sempre all'accelerazione che è la causa del moto.
La seconda legge della dinamica può anche essere generalizzata dicendo che la somma algebrica delle forze attive (che provocano il moto) e delle forze reattive (che si oppongono al moto, come ad es. l'attrito) è uguale alla forza di inerzia (ma).
Negli esercizi, indichiamo generalmente con F le forze attive e con R le forze reattive, dunque è
![]()
questo può essere dedotto da esempi come i seguenti dove identifichiamo come positiva, la direzione positiva dell'asse x e quindi della velocità.
Moto accelerato in assenza di forze reattive.
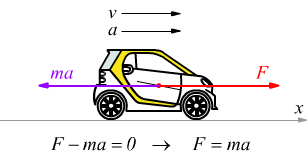
Moto accelerato in presenza di forze reattive.
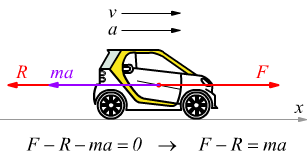
Moto ritardato in presenza solo di forze reattive.

Moto uniforme a velocità costante.
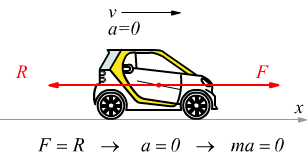
Il fatto di dover attribuire alla forza di inerzia, sempre verso contrario al verso del vettore accelerazione può risultare, talvolta, per qualcuno, un fatto controintuitivo. In tal caso è possibile usare un approccio diverso, basato sul metodo del poligono funicolare che (noi) chiamiamo semplicemente metodo poligonale. Si parte dal presupposto che la forza di inerzia (ma) è la risultante della somma algebrica delle forze attive e reattive applicate al corpo rigido.
Cambiamo esempio ed immaginiamo un disco di hockey su ghiaccio che scivola su un piano ghiacciato, spinto da una forza F che viene contrastata dall'attrito radente sul piano R e dall'attrito dell'aria H. Applichiamo al baricentro G del corpo, tutte le forze, ciascuna col suo verso, mentre sopra al corpo indichiamo il vettore ma con lo stesso verso dell'accelerazione. Da questo disegno estrapoliamo uno schema dove appare lo stesso baricentro G con tutte le forze presenti, collegate a formare un poligono che deve essere chiuso dalla forza di inerzia (ma). All'interno del poligono chiuso indichiamo un verso, per noi arbitrariamente positivo, poi scriviamo un'equazione dove al primo membro compaiono tutte le forze ciascuna col suo segno rispetto a quello convenzionalmente positivo (in questo caso quello orario) e al secondo membro mettiamo 0 (zero).
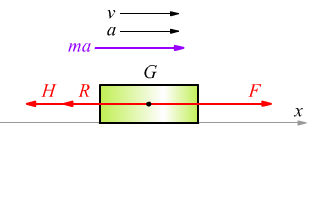
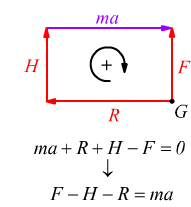
nonostante le apparenze,questo metodo è applicabile anche nel caso in cui appaia solamente la forza attiva F; l'importante è costruire una forma chiusa.
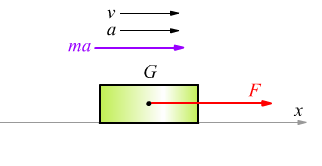
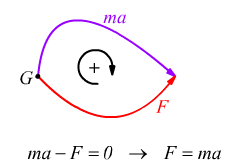
molti degli esercizi riportati, sono stati svolti con questo metodo, è dunque possibile rieseguirli col metodo tradizionale per verificare il risultato.
Un altro esempio di moto traslatorio è quello che riguarda un corpo di peso p=mg disposto su di un piano inclinato di un angolo α rispetto all'orizzontale.
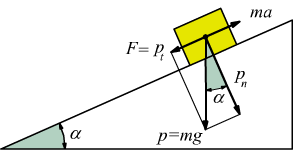
trascurando gli attriti, la forza motrice è costituita dalla forza pt tangenziale al piano, quindi si ha F=pt=p·sinα
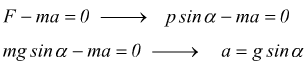
da questa relazione si ottiene l'accelerazione acquisita da un corpo che scende lungo un piano inclinato privo di attriti.
Con la presenza di attrito R nel caso del moto su un piano inclinato si possono presentare le seguenti eventualità:
● Se il moto è in discesa su un piano inclinato; con moto accelerato, sotto l'effetto della componente pt della forza-peso si ha:
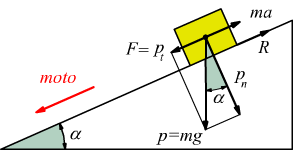

● Se il moto è uniforme (velocità costante) verso l'alto su un piano inclinato; la forza d'inerzia (m·a) è nulla si deve considerare la componente pt della forza peso che si oppone alla salita.

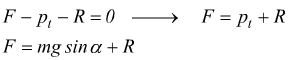
● Se il moto è accelerato verso l'alto su un piano inclinato; la forza d'inerzia non è nulla.
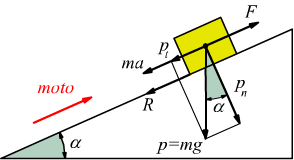
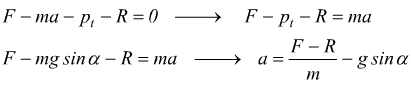
La seconda legge della Dinamica interviene anche se la forza applicata si esprime secondo una direzione diversa alla direzione dello spostamento come si nota nel seguente disegno
in questo caso solo la componente Fx risulterà efficace per far imprimere al blocco una accelerazione, mentre la componente Fy verrà equilibrata da una reazione uguale e contraria del vincolo costituito dal piano di appoggio e si potrà scrivere
![]()
Il corpo, alla fine, acquista una accelerazione tanto maggiore quanto minore è il valore della costante m e prosegue con moto uniformemente accelerato fino a che la forza rimane a esso applicata. Se la forza cessa di agire il corpo prosegue nella stessa direzione con moto rettilineo uniforme. L'esatta tipologia della costante m può essere individuata considerando un corpo di peso (p) che viene lasciato cadere da una determinata altezza nel vuoto. Dagli esperimenti, si sa che esso per effetto della forza di gravità terrestre, esso, acquisterà una certa accelerazione (g) in discesa (l'accelerazione gravitazionale). Dato che in questo caso l'unica forza applicata al corpo è il suo peso (p) la formula precedente può essere riscritta come
![]()

la costante (m) che viene chiamata massa, può essere definita come il rapporto tra il peso di un corpo e l'accelerazione di gravità.
IIIa legge della dinamica (o legge
di azione e reazione).
Ad ogni azione corrisponde una reazione uguale e contraria.
Di quest'ultima legge ci sono molteplici evidenze, ad esempio se un palloncino si sgonfia improvvisamente esso viene spinto in direzione opposta alla direzione da cui esce l'aria dal foro del palloncino stesso.
Osservando la seconda legge di Newton nella forma
![]() con
F=forza motrice ed R=forza resistente.
con
F=forza motrice ed R=forza resistente.
In questa formula il prodotto m·a è da considerare a tutti gli effetti una forza fittizia e (come già detto) viene chiamata forza di inerzia. Il suo segno negativo sta a rappresentare un ostacolo alla realizzazione del moto.
Tutti i corpi tendono, per inerzia, a muoversi con velocità costante. Un corpo inizialmente fermo tende a rimanere fermo.
Si può concludere che: in un corpo rigido, le forze agenti, le eventuali
forze resistenti e le forze di inerzia si fanno equilibrio in ogni istante.
In assenza di forze resistenti la forza di inerzia ha intensità tale
da equilibrare in ogni istante la forza motrice.
Se sono presenti attriti la forza motrice deve equilibrare la risultante
di questi e la forza di inerzia.
La forza di inerzia si manifesta in molte pratiche quotidiane: quando
un veicolo parte di scatto, conducente e passeggeri si sentono spinti
nella direzione contraria a quella del moto, come se nei loro confronti
agisse una forza resistente, questa sensazione è maggiore quanto maggiore
è l'accelerazione del veicolo: questa è una evidenza della forza di
inerzia.
Nelle formule che si sono viste tutte le forze (anche quella di inerzia) si intendono applicate al baricentro del corpo se la forza motrice ha una retta di azione che non passa per il baricentro del corpo rigido considerato, si può produrre la rotazione del mobile (ribaltamento) perchè F ed m·a costituiscono una coppia di forze.
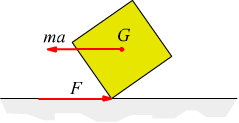
Sintetizziamo, attraverso uno schema, il moto di un corpo dotato di una
massa m=1÷10kg, soggetto ad una forza motrice F=1÷20N, che
viene applicata per un tempo ta=3÷9sec sulla massa stessa,
in direzione positiva dell'asse x. Ipotizziamo l'eventuale presenza di una
forza resistente R che riteniamo attribuibile alla sola resistenza di attrito
del piano (trascuriamo l'attrito viscoso dell'aria). Il valore della forza
resistente R=0%÷75% di F quindi essendo F>R la massa si muoverà
sempre verso destra (direzione positiva asse x). In assenza della forza
resistente, dopo il tempo ta di accelerazione, la forza motrice
cessa la sua azione ed il corpo si muove con moto uniforme (velocità costante)
per un tempo indefinito, percorrendo uno spazio indefinito. In presenza
della forza resistente che è costante alla fine del periodo di accelerazione,
il mobile avrà acquisito una velocità massima che potrà soltanto decrescere
a causa dell'unica forza rimasta R. Si vede come, in tutti i casi, la forza
di inerzia (in giallo)si oppone alla risultante delle forze attive (F in
rosso) e reattive (R in blu) . Se non vi sono forze attive e/o reattive
applicate al corpo, la forza di inerzia cessa di esistere.
: massa 1 kg
: forza 1 N
: R = 0% di F
Partendo dalla seconda legge della dinamica, indicando con FT la forza totale agente su un corpo di massa m. Si ha:
![]() in fase
di accelerazione si ha
in fase
di accelerazione si ha
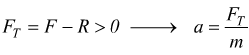
la velocità raggiunta alla fine del tempo di accelerazione ta
può essere calcolata come ![]() (usando le stesse leggi già viste in cinematica).
(usando le stesse leggi già viste in cinematica).
Lo spazio percorso durante la fase di accelerazione è 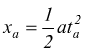
Dopo il tempo di accelerazione ta cessa di esistere la forza motrice F. Se non esiste la forza reattiva R, il mobile continua indefinitivamente il suo moto; in caso contrario, comincia decelerare con accelerazione
 con
il tempo di decelerazione
con
il tempo di decelerazione 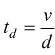 lo
spazio totale può essere calcolato come
lo
spazio totale può essere calcolato come
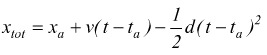 lo
spazio di decelerazione sarà
lo
spazio di decelerazione sarà ![]() .
.
Ad es. con F=1N m=1kg R=15% di F ta=3 sec si avrebbe in fase di accelerazione :

in fase di decelerazione
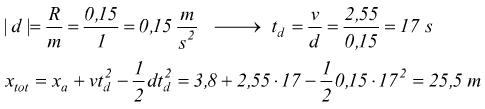
 edutecnica
edutecnica