Decomposizione di forze
Decomposizione di forze parallele e cospiranti
Il tipico caso è costituito da un peso collocato su una trave secondo
lo schema di figura
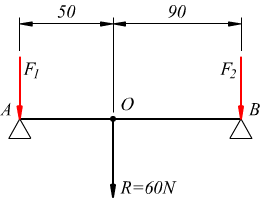
Essa, per le ragioni viste in precedenza sulla composizione delle forze,
può essere assimilata a due forze F1 ed F2 applicate
sui due vincoli A e B con R=F1+F2=60N.
Sappiamo che in questo caso esiste una relazione fra l'intensità delle due
forze F1 ed F2 e la loro distanza dal punto di applicazione
R; in questo caso la forza F1 è quella più vicina alla forza
R per cui sarà la più intensa.
Vale la relazione: 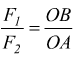 considerando
che F1=R-F2, avremo:
considerando
che F1=R-F2, avremo:
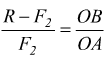 con l'unica incognita
F2...risolvendo:
con l'unica incognita
F2...risolvendo:
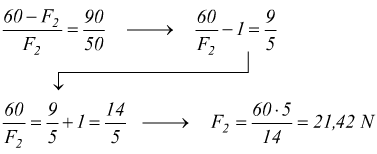
da cui F1=R-F2=60-21,42=38,58 N.
Deomposizione in forze concorrenti
In questo caso possiamo fare l'esempio di un carico appeso ad un cavo incernierato nei punti A e B, al quale è applicata una forza peso F.
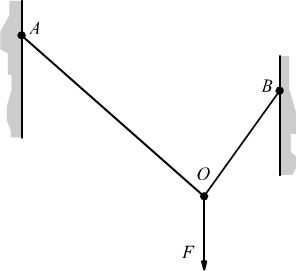
Sarà sempre possibile decomporre la forza F nelle sue due componenti F1 ed F2 lungo le direzioni dei segmenti AO e BO.
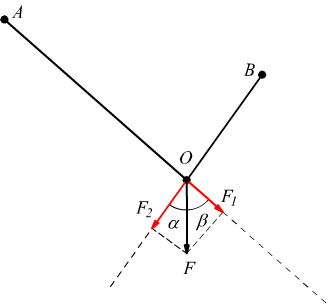
a tal fine diventa essenziale la conoscenza degli angoli α e β
che la forza principale forma con le due direzioni suddette.
un esempio tipico di decomposizione di una forza in due forze concorrenti
è il sistema puntone-tirante: il sistema distribuisce la forza F su due
aste; la forza F1 sul tirante e la forza F2 sul
puntone.
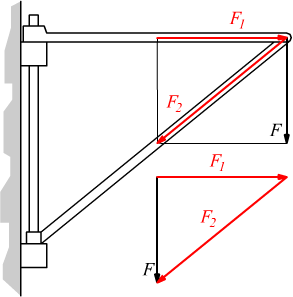
Il tirante sarà sollecitato a trazione, mentre il puntone a compressione.
Anche in questo caso è riconoscibile il triangolo delle forze direttamente
ottenibile dalla regola del parallelogramma.
 edutecnica
edutecnica