Attrito
Quando un corpo si trova appoggiato ad una superficie, in stato di quiete, significa che esiste una condizione di equilibrio tra le forze attive e reattive che interessano tale corpo. Nel caso particolare di una massa m appoggiata su una superficie orizzontale, lo stato di quiete è garantito dalla reazione vincolare V (forza reattiva) della superficie, diretta in senso perpendicolare alla stessa, che va ad equilibrare la forza peso (forza attiva) associata alla massa del corpo ed applicata al baricentro di quest'ultimo
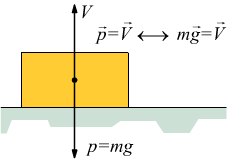
La reazione vincolare V di un appoggio è sempre
perpendicolare al piano costituito dall'appoggio stesso.
La condizione di equilibrio delle forze è, in questo caso, garantita rispetto
all’asse y, ma non è detto che lo sia rispetto all’asse x.
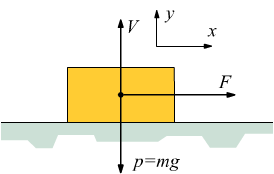
se infatti subentrasse una forza esterna orizzontale F,
sarebbe ragionevole pensare che il corpo possa e riesca muoversi in tale senso,
ma sappiamo benissimo dall’esperienza che non è detto che ciò accada:
dipende quanto attrito c'è tra il corpo e la superficie di appoggio.
Se la superficie è perfettamente levigata (vincolo liscio) l'attrito potrebbe essere
trascurabile o praticamente nullo; il tal caso il corpo può muoversi.
Se la superficie del piano è ruvida, si viene ad instaurare una forza resistente
che si oppone al moto in direzione orizzontale; per muovere il corpo in tal caso,
occorre che la forza F riesca a vincere la forza di attrito che qui,
noi chiamiamo R e che si oppone al senso di F.
Attrito radente
Ogni volta che due corpi sono in contatto, come nel caso di un oggetto
posto su un tavolo, si manifesta una resistenza che si oppone al moto relativo
dei due corpi.
Supponiamo per esempio di spingere un oggetto lungo il tavolo, imprimendogli
una certa velocità. Dopo che la spinta è cessata, l'oggetto rallenta e alla
fine si ferma.
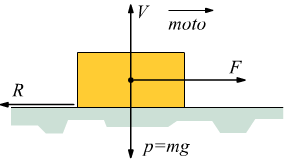
Questa perdita di quantità di moto è indicativa di una forza che si oppone
al moto; la forza è chiamata attrito radente.
Si può sperimentare e dimostrare che la forza massima associata all'attrito
radente che si oppone al moto dell'oggetto vale:
![]() Forza
di attrito radente
Forza
di attrito radente
dove V è la reazione vincolare del piano che
è sempre perpendicolare alla superficie.
In questo caso, che è il più semplice è V=p=mg. Di fatto, V corrisponde
alla forza normale netta che preme sulla superficie. In questo caso particolare,
essa coincide con la forza peso (p):
![]()
Il coefficiente fs è una costante di proporzionalità detta : coefficiente di attrito statico.
Fintanto che la forza esterna applicata F non supera tale valore, il corpo
non riesce a traslare, rimane fermo e la condizione di equilibrio (lungo
la direzione orizzontale) è data in ogni istante da F=R.
Aumentando F, aumenta progressivamente anche R; ma dobbiamo tener conto
che la resistenza di attrito R ha come valore
di soglia Rmax=fsmg oltre il quale R non può
più aumentare.
Appena F supera Rmax ne consegue che la differenza F-R>0:
la risultante delle forze in direzione orizzontale è diversa da zero e per
la seconda legge di Newton il corpo accelera .
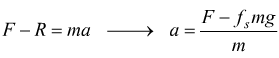
La forza di attrito radente si oppone sempre al moto del corpo ed ha pertanto direzione opposta a quella della velocità (al senso del moto).
Il moto sarà in questo caso uniformemente accelerato (a≠0) e quest'ultima formula rappresenta quella che si può considerare la situazione di 'spunto' cioè la condizione che permette di mettere in moto il grave. Da questo momento in poi, la formula precedente andrebbe corretta sostituendo il coefficiente di attrito dinamico fd al posto del coefficiente di attrito statico fs.
Esistono, infatti, due tipi di coefficiente di attrito. Il coefficiente di attrito statico fs che quando viene moltiplicato per la forza normale al piano (in questo caso mg) dà la forza minima necessaria per mettere in moto il corpo appoggiato, inizialmente alla superficie ed in quiete relativa.
Il coefficiente di attrito dinamico fd
che quando viene moltiplicato per la forza normale, dà la forza necessaria
per mantenere il corpo in moto relativo uniforme (v=cost. con a=0) rispetto
alla superficie.
Dagli esperimenti fatti, risulta sempre fs>fd.
Si deduce che dopo essere riusciti a mettere il moto il corpo applicando
una F>Rmax, per mantenerlo in una condizione di moto uniforme
(v=cost. con a=0) dobbiamo diminuire opportunamente F in modo da soddisfare
la condizione
![]() così
avremo
così
avremo 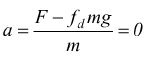
Il comportamento della forza di attrito tra due generiche superfici può essere schematizzato dal seguente diagramma:
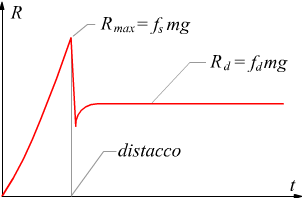
Attenzione : la reazione vincolare V del piano
di appoggio, non sempre coincide esclusivamente con la forza peso.
Ad esempio, nel caso in cui la forza applicata risulti inclinata, essa potrà
essere scomposta nelle sue componenti ortogonali cartesiane ottenendo:
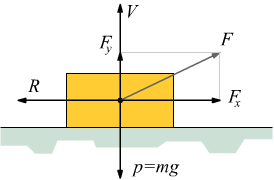
![]() di
conseguenza
di
conseguenza
![]()
e questo ragionamento bisogna farlo anche nel caso di attrito statico (ved.esercizio 4).
Quando abbiamo un corpo a contatto con una superficie soggetto ad una forza ed in presenza di attrito possono, dunque, esservi le seguenti eventualità:
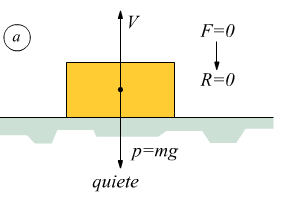
a la forza gravitazionale mg è bilanciata dalla reazione vincolare dell'appoggio V non vi sono forze in direzione orizzontale; il blocco è in equilibrio, fermo.
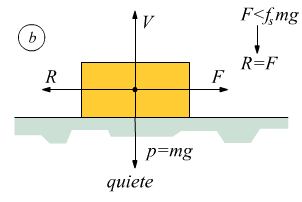
b la forza F applicata
al blocco è bilanciata da una reazione vincolare che agisce in senso opposto:
R (F=R).
Qui si ha con F<R
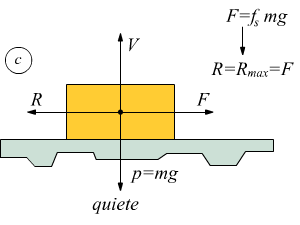
c viene raggiunta la condizione limite dato che F=Rmax=fsmg il blocco è ancora fermo ma è sul punto di staccarsi dalla superficie.
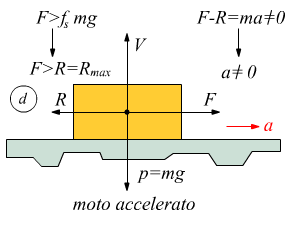
d la forza applicata F ha superato in modulo la resistenza di attrito massima fsmg=Rmax, la essendo F>R la risultante delle forze orizzontali applicate al blocco è diversa da zero. Applicando la seconda legge di Newton
![]()
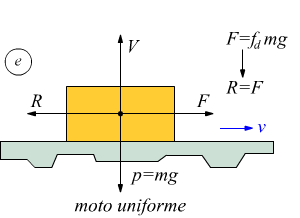
da questo momento, la forza di attrito che si oppone al moto è chiamata forza di attrito dinamica Rd =fdmg
e dopo che il blocco ha iniziato a muoversi, se si vuole che esso abbia un moto uniforme (v=cost. con a=0) è necessario ridurre l'intensità della forza applicata al valore F=Rd=fdmg<fsmg; alcuni valori di riferimento sono i seguenti:
| fs | fd | ||
| Alluminio | Alluminio | 1.05÷1.35 | 1.40 |
| Alluminio | Acciaio dolce | 0.61 | 0.47 |
| Ghisa | Ghisa | 1.10 | 0.15 |
| Rame | Acciaio dolce | 0.53 | 0.36 |
| Vetro | Vetro | 0.9÷1.00 | 1.00 |
| Grafite | Grafite | 0.10 | 0.10 |
| Acciaio dolce | Ottone | 0.51 | 0.44 |
| Acciaio dolce | Acciaio dolce | 0.74 | 0.57 |
| Gomma | calcestruzzo | 1.0 | 0.80 |
| Teflon | Teflon | 0.04 | 0.04 |
Attrito e piano inclinato
I problemi di Fisica col piano inclinato, in presenza di attrito vengono assegnati molto di frequente
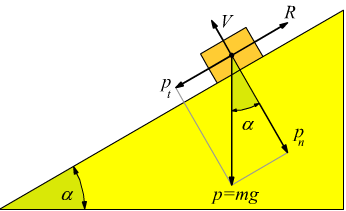
si riconosce che la forza peso p, può essere scomposta in due componenti ortogonali tra loro: la componente tangenziale alla direzione del piano pt e la componente normale (perpendicolare) al piano pn.

la forza di attrito vale in questo caso ![]() se
se
![]() il
grave comincia a scivolare in discesa.
il
grave comincia a scivolare in discesa.
il grave resta fermo fintanto che 
Attrito volvente
Questo è un tipo di attrito che si ha quando un corpo cilindrico ruota su un piano
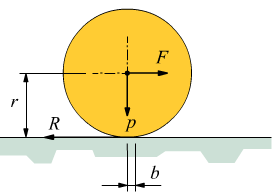
Considerata la semilunghezza b di una lunghezza simmetrica 2b rappresentativa la lunghezza della superficie di contatto, l'equazione di equilibrio alla rotazione è:
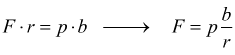 il
coefficiente
il
coefficiente 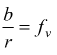 è
il coefficiente di attrito volvente
è
il coefficiente di attrito volvente
In condizioni di moto uniforme F=R, per cui: ![]()
L'attrito volvente è proporzionale alla pressione normale e dipende dalla
natura delle superfici a contatto. Valori tipici dell'attrito volvente sono:
fv=0,015÷0,035 autoveicoli su strada
fv=0,002÷0,003 veicoli su rotaia
Attrito nei fluidi
Quando un corpo si muove in un fluido, che può essere un gas o un liquido, con velocità relativamente bassa , la forza di attrito si può approssimare supponendo che essa sia proporzionale ed opposta alla velocità.
![]()
La relazione appena scritta è nota come legge di Stokes; in essa il coefficiente K dipende dalla forma del corpo, ad esempio nel caso di una sfera, calcoli abbastanza laboriosi indicherebbero K=6πr (con r=raggio della sfera).
Il coefficiente η chiamato anche viscosità dipende dall'attrito interno del fluido. La viscosità nei liquidi diminuisce all'aumentare della temperatura, mentre nel caso dei gas, il coefficiente η aumenta all'aumentare della temperatura.
Quando un corpo si muove attraverso un fluido viscoso sotto l'azione di una forza F, l'equazione del moto viene scritta come
![]()
Supponendo che la forza F sia costante, l'accelerazione a produce un aumento continuo di v ed un aumento corrispondente dell'attrito col fluido, finchè, ad un certo punto il termine al secondo membro diventa zero: allora anche l'accelerazione è zero e non si ha un ulteriore aumento di velocità, l'attrito col fluido essendo esattamente controbilanciato dalla forza applicata.
Il corpo, continua a muoversi nella direzione della forza con una velocità costante detta velocità limite o di regime che è data dalla formula
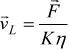
La velocità limite dipende da η e K; cioè dalla viscosità del fluido e dalla forma del corpo. In caduta libera per gravità con F=mg diventa
![]()
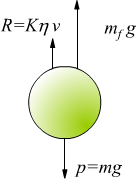
quest'ultima espressione deve essere corretta per la spinta idrostatica esercitata dal fluido che, in accordo col principio di Archimede, è uguale al peso del fluido spostato dal corpo. Se mf è la massa del fluido spostata dal corpo, il suo peso è mfg coincide con la spinta di Archimede verso l'alto , in questo modo la spinta idrostatica risultante sarà mg-mfg; in pratica risulta
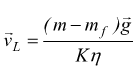
 edutecnica
edutecnica