Rotazione
La rotazione di un corpo è un fenomeno fisico che può essere osservato frequentemente. Esso richiede tuttavia alcuni presupposti: per far entrare in rotazione un corpo rigido (indeformabile) occorre una forza ed un vincolo. La forza applicata, causa una variazione di velocità di quel corpo. Dunque se il corpo è inizialmente fermo esso può iniziare a ruotare. Il vincolo e indispensabile; esso costituisce il fulcro cioè il punto fisso della rotazione : deve impedire la traslazione e lasciare solo un grado di libertà per la rotazione.
Abbiamo esperienza quotidiana di moti puramente rotazionali come nel atto di aprire una porta, serrare un dado con una chiave inglese, azionare una manovella o la manopola di un rubinetto. In tutti questi casi stiamo applicando una forza rispetto ad un punto fisso o a un asse detto anche fulcro di rotazione. In altri termini stiamo applicando il momento di una forza.
L’apertura di una porta è un classico caso di applicazione di un momento di una forza.
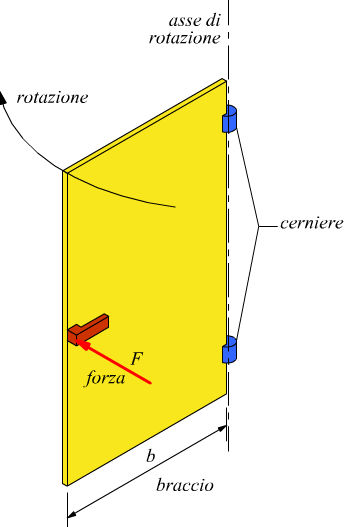
Affinché un corpo al quale è applicata una forza possa soltanto ruotare occorre sia presente un vincolo. Il vincolo può assumere diverse forme nel caso di una porta o dell’anta di un armadio o di un pensile da cucina il vincolo si chiama cerniera o cardine. Se applichiamo una forza alla maniglia di una porta questa entra in rotazione rispetto ad un asse ideale passante per i suoi cardini. Il momento applicato è dato dal prodotto della forza F per la distanza dal fulcro della rotazione che corrisponde all’asse dei cardini; questa distanza viene denominata braccio della forza. In meccanica viene spesso usata la locuzione “momento torcente”.
Momento di una forza
Consideriamo una forza F agente su un corpo C che può ruotare attorno al punto O come si vede nel disegno qui sotto.
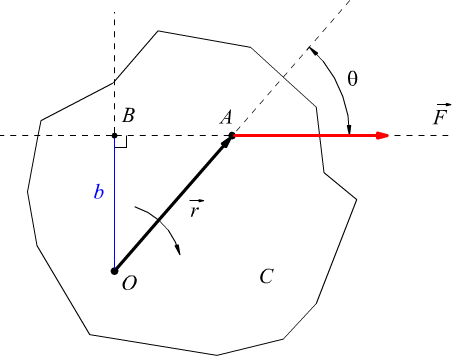
Se la forza non passa per O, l'effetto risultante è quello di una rotazione del corpo attorno al polo O.
L'esperienza quotidiana ci suggerisce che l'efficacia di F per quanto riguarda la rotazione del corpo aumenta con l'aumentare della minima distanza chiamata braccio $b = \ov {OB}$ fra il punto O e la retta di azione della forza. Per esempio, quando apriamo una porta, noi tiriamo o spingiamo sempre il più lontano possibile dai cardini, e tentiamo di mantenere la direzione di spinta o di tiro perpendicolare alla porta. Questa esperienza suggerisce pertanto la convenienza di definire una quantità fisica M, che possiamo chiamare momento mediante la relazione
$$M=Fb$$
cioè momento = forza × braccio; di conseguenza, il momento deve essere espresso dimensionalmente come il prodotto dell'unità di forza per l'unità di distanza. Nel sistema internazionale il momento è espresso in newton×metro, o N·m.
Osservando il disegno precedente si ha $b = r·sinθ$ possiamo allora scrivere
$M=Fr\,sinθ$
Essendo $F↖{→}$ ed $r↖{→}$ due vettori mentre $θ$ è l’angolo formato tra la direzione della forza e la direzione del vettore posizione $r↖{→}$. questa relazione può essere facilmente inquadrata come un prodotto vettoriale:
$M↖{→}=r↖{→}×F↖{→}$
dove $r↖{→}$ è il vettore posizione, relativo al polo O, del punto di applicazione A su cui la forza $F↖{→}$ agisce.
Tenendo presenti le proprietà del prodotto vettoriale, il momento è rappresentato da un vettore perpendicolare sia ad $r↖{→}$ che ad $F↖{→}$; vale a dire, perpendicolare al piano passante per $r↖{→}$ e per $F↖{→}$, e diretto come il senso di avanzamento di una vite destrorsa che ruota nello stesso senso della rotazione prodotta da F attorno al polo O, come indicato nello schema qui sotto.
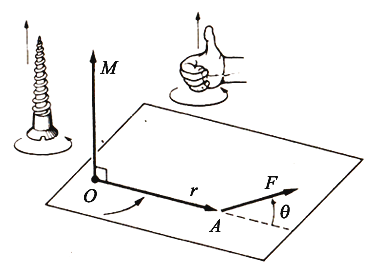
nello spazio tridimensionale avremo : $r↖{→}=i↖{\^}x+j↖{\^}y+k↖{\^}z$ ed $F↖{→}=i↖{\^}F_x+j↖{\^}F_y+k↖{\^}F_z$. Usando il calcolo matriciale:
$$M↖{→}=r↖{→}×F↖{→} = [ \table i↖{\^},j↖{\^},k↖{\^}; x,y,z;F_x,F_y,F_z]= i↖{→}[ \table y,z; F_y,F_z]-j↖{→}[ \table x,z; F_x,F_z]+k↖{→}[ \table x,y; F_x,F_y] $$
$M↖{→}=i↖{\^}(yF_z-zF_y)+j↖{\^}(zF_x-xF_z)+ k↖{\^}(xF_y-yF_x)$
In particolare, se tanto $r↖{→}$ che $F↖{→}$ giacciono nel piano XY, $z = 0$ ed $F_z$ = 0, cosicchè $M↖{→}=k↖{\^}(xF_y-yF_x)$ è parallelo all'asse Z. In modulo, si ha semplicemente $M=(xF_y-yF_x)$.
Nello schema seguente riassumiamo le nozioni di braccio e momento di una forza.
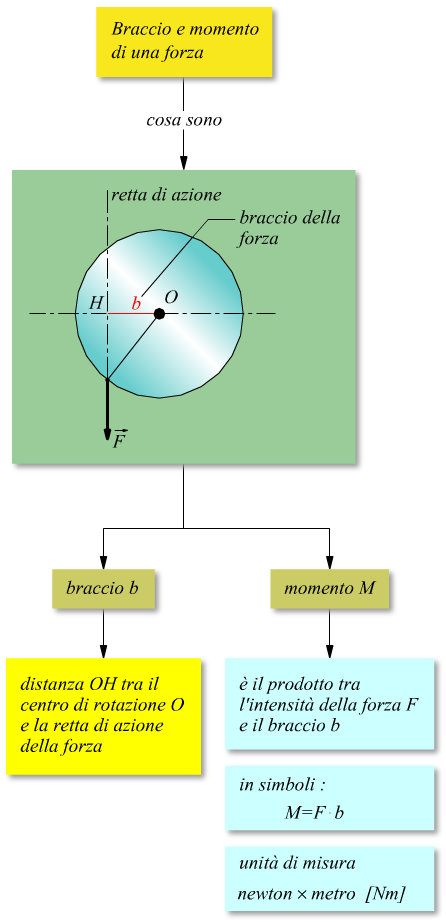
Da questa immagine risulta evidente come il braccio della forza sia la minima distanza tra la retta di azione della forza stessa e il fulcro, punto fisso della rotazione.
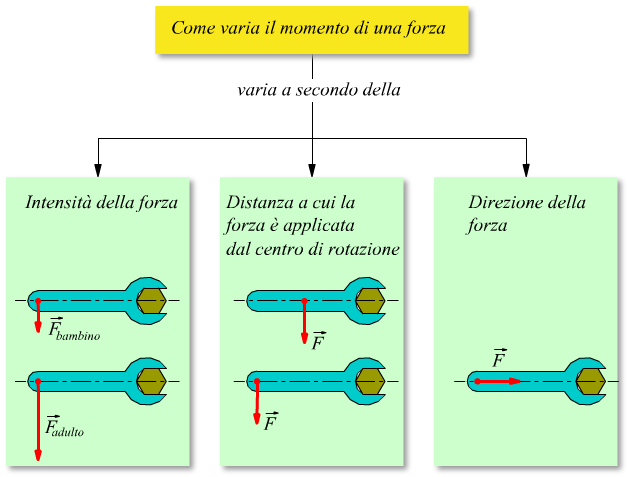
Come varia il momento di una forza
Per imprimere una rotazione tramite il momento di una forza è di particolare rilevanza il modo in cui viene applicata tale forza. Essendo le grandezze fisiche coinvolte dei vettori l’efficacia del momento applicato è anche funzione di variabili geometriche.
Immaginiamo di dover svitare un dado tramite una chiave inglese.
1 Un adulto fa ruotare il dado più facilmente di un bambino, questo perché l’intensità della forza applicata è maggiore.
2 Una forza più distante dal fulcro di rotazione, cioè dal dado, fa ruotare quest’ultimo con maggior facilità della stessa forza applicata in un punto vicino al dado.
3 Più la forza è diretta verso il centro della rotazione più è difficoltosa la rotazione di questo.
Questi fatti sperimentali sono riassunti nella seguente mappa concettuale.
Segno del momento
Il momento di una forza può essere considerato positivo o negativo a secondo del senso di rotazione. Convenzionalmente il momento è positivo se produce una rotazione antioraria rispetto all’osservatore, In tal caso il vettore momento sarà orientato perpendicolarmente al piano di giacitura della forza e del braccio e il verso sarà diretto verso l'osservatore.
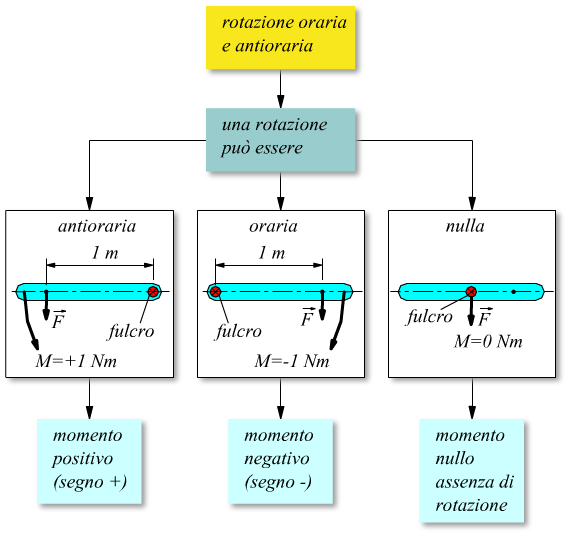
Viceversa, il momento è negativo in caso di rotazione oraria, e il vettore momento $M↖{→}$ sarà diretto con verso contrario all’osservatore.
In base agli schemi illustrati si conclude che il momento di una forza è nullo quando la direzione della forza passa per il punto fisso della rotazione perchè in tal caso il braccio è nullo e il prodotto F·b vale zero.
Regola della mano destra per il momento
Una semplice regola pratica che permette di stabilire direzione e verso di un momento di forze è la regola della mano destra: se si dispongono le dita secondo il senso di rotazione della coppia, il pollice indica la direzione e il verso del momento.
Nel disegno seguente è illustrata laregola della mano destra momento di una forza
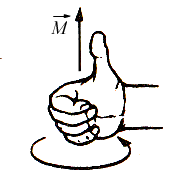
In base a questa semplice regola pratica si riesce a stabilire direzione e verso del un momento di una forza : se si dispongono le dita secondo il senso di rotazione della forza, il pollice indica la direzione e il verso del momento.
Momento di più forze concorrenti
Come nel caso delle forze e più in generale dei vettori, si ha spesso la necessità di valutare il momento risultante di un sistema di forze concorrenti rispetto ad un dato polo.
In tal caso è possibile applicare il teorema di varignon.
Ipotizzando di avere un sistema di forza complanari F1 F2..Fn ; il teorema di Varignon afferma che
In un sistema di forze complanari la somma algebrica dei momenti delle singole forze, rispetto ad un generico punto P del piano, è uguale al momento della risultante del sistema di forze, valutato rispetto allo stesso punto.
Se pensiamo ad un sistema con tre forze F1 F2 ed F3 valutando i momenti rispetto ad un polo scelto arbitrariamente:
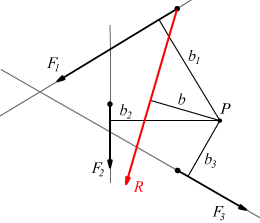
$M=M_1+M_2+M_3$
o anche
$M=Rb=b_1F_1+b_2F_2+b_3F_3$
Il teorema di Varignon anche chiamato teorema dei momenti è molto utile per stabilire rapidamente la posizione della risultante di un sistema di forze parallele.
Se ci riferiamo al sistema di forze qui sotto disegnato, scelto arbitrariamente un polo P sulla congiungente i punti di applicazione delle forze F1 F2 ed F3 :
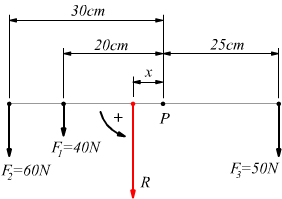
$M_1=F_1·b_1=40·20=800$ Ncm
$M_2=F_2·b_2=60·30=1800$ Ncm
$M_3=F_3·b_3=50·25=1250$ Ncm
il momento risultante del sistema di forze è :
$M_R=M_1+M_2-M_3=800+1800-1250=1350$ Ncm
con $R=F_1+F_2+F_3=60+40+50=150$ N essendo poi
$M_R=R·x=150·x=1350$ Ncm avremo
$$x=M_R/R=1350/150=9$$ cm
Nello schema sottostante, si valuta il momento M di una forzaF (in verde) rispetto al polo di coordinate (0,0).
Si può modificare la posizione di F spostando la sua coda o la sua punta
sul piano.
Lo spostamento $r$ è disegnato in viola. $|r|$
è la lunghezza (modulo) di $r↖{→}$ mentre $∠r$
è l'angolo che lo spostamento $r↖{→}$ forma con l'asse orizzontale (x).
Nella rappresentazione si assume una proporzionalità $1m ∝ 1px$.
Allo stesso modo $|F|$ è il modulo della forza
F mentre $∠F$ è l'angolo che F forma con
l'orizzontale x.
Nei dati, θ è l'angolo reciproco tra $F↖{→}$ e $r↖{→}$ :
$θ=∠F-∠b$
ed è proprio questo angolo che deve essere usato nella formula per il calcolo del momento. Si nota come in questo caso manteniamo $r≡b$ mentre per calcolare il momento usiamo la forma equivalente
$M↖{→}=r↖{→}×F↖{→}=F_{⊥}r=Fr\,sinθ$
: x [m] : |F| [N] : |r| [m] : θ [deg]
: y [m] : ∠F [deg] : ∠r [deg]
Argomenti correlati:
 edutecnica
edutecnica