Ciclo di Carnot

Un ciclo fondamentale per lo studio della termodinamica è il ciclo di Carnot, detto anche ciclo di massimo rendimento. Esso viene eseguito da una macchina termica ideale ed è costituito da due trasformazioni adiabatiche e da due trasformazioni isoterme.

Ipotizziamo di avere 1kg di gas nelle condizioni iniziali P₁V₁T₁ contenuto in un cilindro in cui scorre uno stantuffo con possibilità di riscaldare, raffreddare e isolare adiabaticamente il gas.

L₁₂ (area 122'1') :espansione isoterma, il lavoro è positivo perchè il volume aumenta
L₂₃ (area 233'2') :espansione adiabatica, il lavoro è positivo perchè il volume aumenta
L₃₄ (area 344'3') :compressione isoterma, il lavoro è negativo perchè il volume diminuisce
L₄₁ (area 411'4') :compressione adiabatica, il lavoro è negativo perchè il volume diminuisce.

Si deduce che il lavoro complessivo espresso dal ciclo è positivo.
Osservando poi il diagramma entropico e tenendo conto che ΔQ=T·ΔS si ricava

Q₁₂ (area 122'1') :espansione isoterma, il calore scambiato è positivo perchè l'entropia aumenta
Q₂₃ (area nulla) :espansione adiabatica, i processi adiabatici prevedono ΔQ=0.
Q₃₄ (area 341'2') :compressione isoterma, il calore scambiato è negativo perchè l'entropia diminuisce.
Q₄₁ (area nulla) :compressione adiabatica, come tale ΔQ=0.

Indicando con Q_s il calore scambiato con la sorgente termica alla temperatura superiore e con Q_i quello scambiato con la sorgente a temperatura inferiore si ha

per definizione il rendimento è

ma osservando il disegno

Alle stesse conclusioni si arriva osservando le trasformazioni sul piano PV.
Il ciclo di Carnot è un ciclo simmetrico; i cicli simmetrici sono costituiti da trasformazioni a due a due uguali in modo da poter chiudere il percorso. Una rappresentazione del processo e riportato in questa pagina. Per un ciclo simmetrico è possibile dimostrare che è

Ricordiamo che per una trasformazione isoterma è

Ricordiamo che durante una trasformazione isoterma ΔU=0 non vi è variazione di energia interna del sistema, quindi il primo principio della termodinamica diventa Q=L

Q_s>0 perché V₂>V₁.

poi avremo ma a noi serve il modulo di |Q_i| →

sapendo che per i cicli simmetrici valgono le relazioni dunque

sostituendo nella formula del rendimento

T₁=T_s temperatura della sorgente superiore di calore
T₃=T_i temperatura della sorgente inferiore di calore

v₁ [m³/kg]

v₂ [m³/kg]

v₃ [m³/kg]

p_max [kPa]

Ciclo Stirling

Il ciclo Stirling (1816) è costituito da quattro trasformazioni reversibili, rappresentate nel disegno

A.) trasformazione 12, espansione isoterma alla temperatura T₁
B.) trasformazione 23, trasformazione isocora da T₂ a T₃
C.) trasformazione 34, compressione isoterma alla temperatura T₃
D.) trasformazione 41, isocora da T₄=T₃ a T₁.

come nel caso del ciclo di Carnot

mentre

qui proprio perché è evidente dal disegno che V₃=V₂ e V₄=V₁.

per quanto riguarda le isocore, trattandosi di trasformazioni a volume costante, bisogna usare il calore specifico appropriato (a volume costante).

quindi

nell'isocora 23 il gas cede una certa quantità di calore che viene riassorbita in ugual misura nella trasformazione 41.

Come nel caso del ciclo precedente si avrà

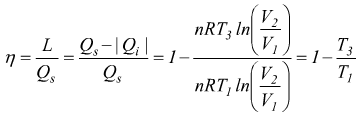
viene ottenuta una formula per il rendimento identica al ciclo di Carnot

La macchina di Stirling ebbe una certa diffusione per diversi anni, ma in seguito all'avvento delle macchine a vapore e a quelle a combustione interna, cadde in disuso.

Argomenti correlati: