Gas ideali
Per lo studio dei gas si considera un modello chiamato
gas perfetto per il quale si assume che tutte le molecole abbiano
la stessa energia cinetica, ed inoltre siano nulle tutte le forze di
attazione tra le stesse molecole.
L'equazione di stato del gas perfetto
descrive lo stato in cui si trova una determinata massa di gas:
![]()
P=pressione in pascal [Pa]
V=volume in m3
T=temperatura in gradi Kelvin K
R=costante universale dei gas R=8,314 J/mol°K
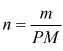 numero
di moli con m=massa [ g ] e PM=peso molecolare [ g/mol ]
numero
di moli con m=massa [ g ] e PM=peso molecolare [ g/mol ]
quest'ultimo (nota la formula della sostanza) può essere dedotto dalla tavola periodica oppure dalla seguente applicazione.
: P: V
: T
: m
: PM [ g/mol ] [ kg/kmol ]
Questa, è la versione più comune dell'equazione di stato dei gas, e viene usata prevalentemente in ambito chimico. Può essere usata una variante di questa equazione (ad es. in impiantistica, dove il numero di sostanze utilizzate è limitato) qualora risulti comodo usare la massa del gas piuttosto che il numero di moli. Ponendo
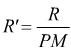 in
questo modo l'equazione di stato dei gas ideali diventa
in
questo modo l'equazione di stato dei gas ideali diventa
![]()
P=pressione in pascal [Pa]
V=volume [ m3 ]
m=massa [kg]
R'=costante specifica del gas (riferita ad 1kg di massa) [ J/kg°K ]
T=temperatura in gradi Kelvin [ K ]
I valori di R' per alcuni tipi di gas sono:
| Gas | k (=cp/cv) | cp [kJ/kg°K] | cv [kJ/kg°K] | R' [J/kg°K] |
| Aria (fino a 300°C) | 1,4 | 1,025 | 0,717 | 287,1 |
| Elio | 1,66 | 5,232 | 3,140 | 2077,7 |
| Ossigeno | 1,4 | 0,908 | 0,649 | 259,8 |
| Idrogeno | 1,407 | 14,274 | 10,13 | 4125,5 |
| Ossido di carbonio | 1,4 | 1,013 | 0,720 | 296,8 |
| Azoto | 1,4 | 1,034 | 0,737 | 296,7 |
| Anidride carbonica | 1,3 | 0,879 | 0,670 | 188,9 |
| Ammoniaca | 1,29 | 2,218 | 1,716 | 488,2 |
| Metano | 1,31 | 2,47 | 1,925 | 518,3 |
| Vapore (100°C) | 1,3 | 2,009 | 1,549 | 461,6 |
| Propano | 1,127 | 1,667 | 1,479 | 188,6 |
| Argon | 1,329 | 0,520 | 0,391 | 208,1 |
La costante R è la costante universale dei gas; essa viene definita secondo il sistema internazionale alla temperatura T=273,15 K=0°C alla pressione di P=1 atm=101325 pa. In queste condizioni 1 kmole di gas occupa un volume V=22,414m3, questo vale per tutti i gas.

Per passare dalla costante riferita alla kmole alla costante riferita alla massa bisogna dividere la R per il peso molecolare del gas. La costante R per l'ossigeno O2:
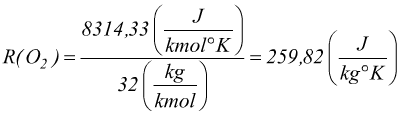
La costante R per la CO2:
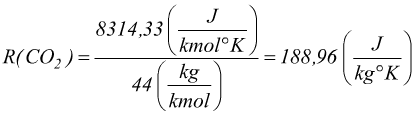
: V
: T
: m
: R' [ J/kg°K ]
Qualche difficoltà ci può essere nelle unità di misura della pressione; l'importante è ricordarsi che:
![]() con
con ![]()
Nello svolgere i problemi poi, può essere opportuno usare il volume specifico e allora una forma conveniente dell'equazione di stato è:
![]()
p= pressione [kPa]
v= volume specifico [m3/kg]
R' = costante specifica del gas [kJ/kg°K]
T= temperatura [K]
facendo attenzione che usando questa forma, anche il lavoro ed il calore saranno specifici, cioè riferiti ad 1kg di gas.
Per una massa unitaria m=1kg si ha
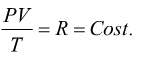
Che può mettere in relazione due stati termodinamici della stessa massa di gas:
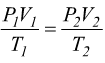
nota come legge di Gay-Lussac; le sue varianti sono:
![]() per
trasformazioni isoterme (T=cost.) (legge
di Boyle)
per
trasformazioni isoterme (T=cost.) (legge
di Boyle)
 per
trasformazioni isocore (V=cost.)
per
trasformazioni isocore (V=cost.)
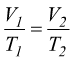 per
trasformazioni isobare (P=cost.)
per
trasformazioni isobare (P=cost.)
Un piano privilegiato per le trasformazioni termodinamiche è il piano
P-V
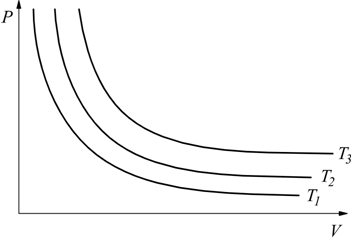
sul quale abbiamo riportato il comportamento di alcune isoterme.
Energia interna
Ogni sistema ha un suo contenuto di energia interna (U) nella quale si sommano tutte le forme di energia legate al suo stato, come l'energia dovuta ai legami tra nucleo ed elettroni, tra gli atomi, energia cinetica delle molecole, insomma tutte le energie delle sue componenti microscopiche.
Il valore assoluto dell'energia interna U di un sistema in un determinato stato non è mai nota, ma per la termodinamica questo non è importante, è invece importante conoscere la differenza ΔU di energia interna di un sistema prima e dopo una trasformazione.
In ogni caso, per un gas perfetto l'energia interna è data dal prodotto tra l'energia cinetica media di una molecola Km e il numero di molecole che compongono il sistema.
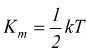 energia
cinetica media di una molecola
energia
cinetica media di una molecola
k=costante di Boltzmann=1,38·10-23 [ J/°K
]
T=temperatura [ °K ]
se indichiamo con N il numero di molecole che costituiscono il sistema:
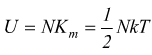
Primo principio della Termodinamica
Quando un gas acquisisce una quantità di calore
Q aumenta la sua temperatura e varia la sua energia
interna
U [ J ].
L'energia interna di un gas U=U(T) è funzione della temperatura, di
conseguenza se la temperatura di un gas rimane costante, rimane costante
anche la sua energia interna. ( ΔU=0).
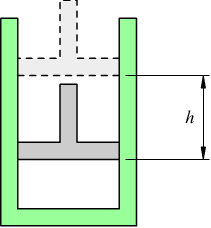
Ipotizziamo che un gas sia contenuto in un cilindro nel quale si possa muovere un pistone (senza attrito). Se il gas si espande, esegue un lavoro dato dal prodotto fra la forza F esercitata dal gas e lo spostamento h:
![]() ma
F vale
ma
F vale ![]()
dove P è la pressione del gas ed S la superficie del cilindro. Mentre lo spostamento h del pistone è dato da:
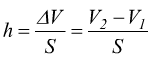 per
cui il lavoro vale:
per
cui il lavoro vale:
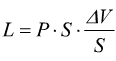 quindi
quindi
![]()
Convenzionalmente è positivo il lavoro di espansione ed è negativo il lavoro di compressione.
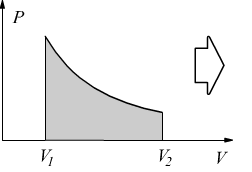
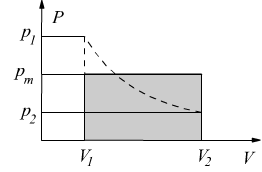
Il lavoro è dato dall'area sottesa fra la curva di trasformazione e l'asse delle ascisse. Può anche essere espresso dall'area del rettangolo:
![]()
dove pm è la pressione media fra p1 e p2.
Il fenomeno considerato può essere ottenuto fornendo al gas una determinata
quantità di calore Q.
Se un gas passa da uno stato iniziale ad uno stato finale, una parte della
quantità di calore fornita si trasforma in lavoro, un'altra parte in variazione
dell'energia interna del gas:
![]()
Questa formula rappresenta
il primo principio della
Termodinamica basato sulla legge di conservazione dell'energia:
esso stabilisce che l'energia può essere solo convertita da una forma
ad un'altra ma non può essere ne creata ne distrutta. Se il gas
in questione compie una serie di trasformazioni che riportano il gas
nelle condizioni iniziali (ciclo termodinamico) si ha il principio di
equivalenza Q=L. Per convenzione
Q > 0 quando il calore viene trasferito dall'ambiente al sistema.
Q < 0 quando il calore viene trasferito dal sistema all'ambiente.
L > 0 quando il lavoro viene fatto dal sistema sull'ambiente (espansione).
L < 0 quando il lavoro viene fatto dall'ambiente sul sistema (compressione).
La quantità di calore Q può essere ottenuta
attraverso la nota formula
del calore specifico Q=m·c·ΔT già considerata,
dove c può essere il calore specifico a pressione costante cp
oppure il calore specifico a volume costante cv , a secondo
di come avviene la trasformazione.
Entalpia ed Entropia
Il primo principio della termodinamica afferma:
![]()
per una trasformazione isobara
![]()
![]()
![]()
Per opportunità viene introdotta una nuova grandezza fisica chiamata entalpia
![]()
misurata in Joule convenzionalmente posta U=0 per T=273 K.
Essendo :
![]()
In una trasformazione isobara la variazione
di entalpia coincide col calore scambiato.
L'entalpia è il contenuto termico di un fluido che tiene conto oltre
che dell'energia interna U anche delle condizioni di pressione e volume
in cui si trova la sostanza.
Essa è una variabile di stato e la sua variazione dipende solo dai valori
dello stato finale e dello stato iniziale, non dal percorso seguito
dalla trasformazione.
ΔH<0 :il processo è esotermico e il sistema cede energia all'ambiente,
ΔH>0 :il processo è endotermico e il sistema acquisisce energia
all'ambiente.
Per una trasformazione isoterma ( anche a pressione e volume costante ) si ha:
![]()
In generale una trasformazione che ha lo scopo di produrre lavoro meccanico
da energia termica è interessata da attriti e perdite di varia natura,
questo motivo viene chiamata trasformazione 'irreversibile'.
Soltanto eliminando tutti gli attriti (al limite) si possono ottenere
trasformazioni 'reversibili'.
La funzione di stato usata in termodinamica collegata a queste caratteristiche
di reversibilità o irreversibilità è l'entropia, definita come:
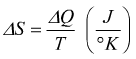
Il fatto di interesse non è il valore assoluto dell'entropia in un dato
stato, ma la variazione di entropia S che vi può essere a seguito di
una trasformazione.
Ogni trasformazione reale, avviene con un aumento di entropia. Per l'adiabatica
ΔQ=0 → ΔS=0.
L'adiabatica è una trasformazione isoentropica.
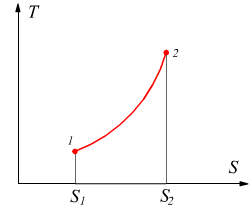
Diagramma entropico
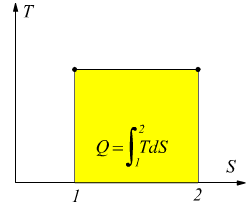
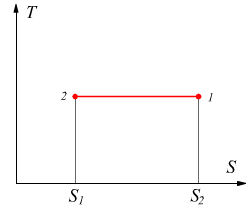
L'entropia è una funzione di stato e può, dunque, essere usata come coordinata nei diagrammi delle proprietà di una data sostanza. Il diagramma entropico ha l'entropia S sull'asse delle ascisse e sull'asse delle ordinate la temperatura T; è particolarmente utile per evidenziare il calore scambiato nelle trasformazioni reversibili, infatti dalla definizione di entropia si ha

Nel caso particolare di una trasformazione isoterma il calore scambiato è costituito dall'area rettangolare di lati T e ΔS.
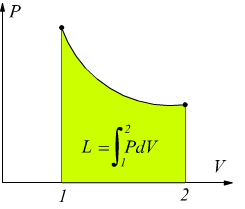
Il risultato è analogo a quello ottenuto sul piano PV dove le aree sottese rappresentano il lavoro scambiato dal sistema.
Dato che T è in °K sarà sempre positivo, il calore scambiato durante la trasformazione reversibile risulterà positivo quando l'entropia aumenta, mentre sarà negativo quando l'entropia diminuisce. Queste considerazioni sono valide solo nel caso in cui le trasformazioni effettuate siano reversibili; nel caso in cui le trasformazioni siano irreversibili noi conosciamo solo lo stato iniziale e quello finale, non abbiamo alcuna conoscenza dell'esatto percorso compito nel passaggio tra i due stati; a regola le trasformazioni irreversibili non potrebbero nemmeno essere disegnate sui piani termodinamici.
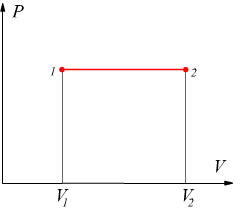
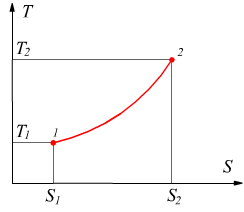
Trasformazione isobara
E' una trasformazione reversibile eseguita a pressione costante data dall'equazione
 con
con ![]() ed inoltre
ed inoltre ![]() riferendoci
ad una mole di gas
riferendoci
ad una mole di gas
![]()
![]()
Trasformazione isocora
Si tratta di una trasformazione reversibile eseguita a volume costante, dunque, risulta L=0 . Inoltre si ha:
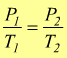 con
con ![]()
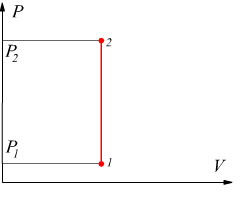

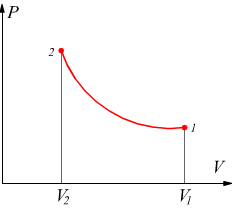
Trasformazione isoterma
Si tratta di una trasformazione reversibile eseguita a temperatura costante caratterizzata dall'equazione
![]()
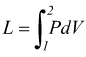 sostituendo
la pressione generica
sostituendo
la pressione generica 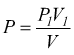
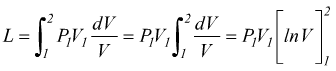 cioè
cioè
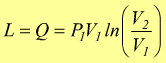 oppure
oppure 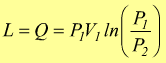 dato
che ΔU=0
dato
che ΔU=0
Per quanto detto prima : P·ΔV=R·ΔT dunque
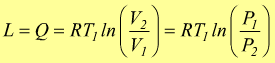
Trasformazione adiabatica
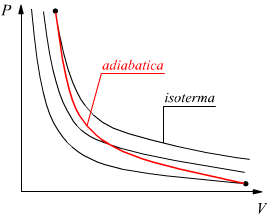
E' una trasformazione reversibile dove non si verifica scambio di calore con l'ambiente dunque, Q=0 e dal primo principio risulta ΔU=- L .
![]()
con cp=cv+R
(relazione di Mayer) e 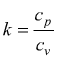 quindi
quindi
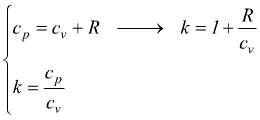 da
cui risulta
da
cui risulta 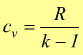 e
allo stessso modo
e
allo stessso modo 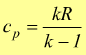
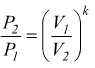 per
una mole di gas
per
una mole di gas 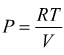 sostituendo
P si avrebbe
sostituendo
P si avrebbe
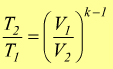 in
modo analogo si potrebbe ottenere
in
modo analogo si potrebbe ottenere 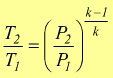
se poniamo C=costante 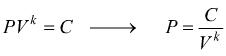
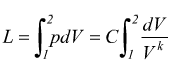
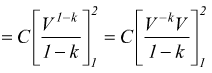
ma dato che è anche 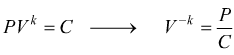 avremo
avremo
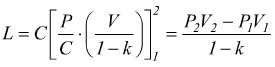 che
si può riscrivere come
che
si può riscrivere come 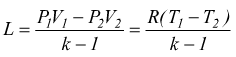
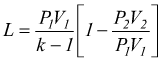 ma
se è
ma
se è 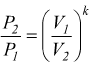 si
ha
si
ha
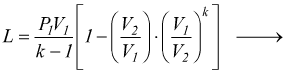
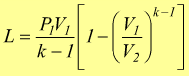
in modo analogo si potrebbe dimostrare 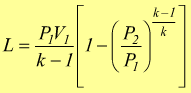
In base alla teoria cinetica dei gas si ha:
| gas | cv | cp | k |
| monoatomici | 3R/2 | 5R/2 | 1,67 |
| biatomici | 5R/2 | 7R/2 | 1,40 |
| poliatomici | 3R | 4R | 1,33 |
Trasformazione politropica
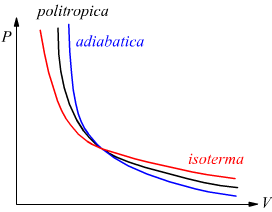 E'
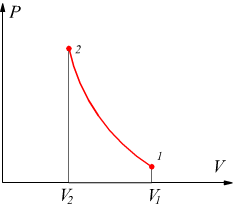
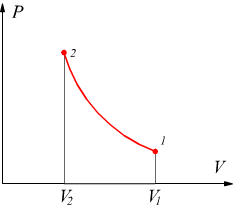
una trasformazione reversibile che sul piano PV ha un andamento intermedio
tra una adiabatica ed una isoterma dove vale la relazione
E'
una trasformazione reversibile che sul piano PV ha un andamento intermedio
tra una adiabatica ed una isoterma dove vale la relazione
![]() 1<n<k
1<n<k
Sempre riferendoci ad una mole di gas perfetto dove vale la relazione PV=RT si trovano altre relazioni equivalenti come
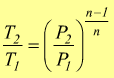 oppure
oppure
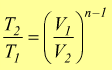
Le equazioni del lavoro sono simili a quelle dell'adiabatica basta sostituire n a k.
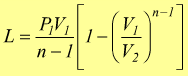 o
o 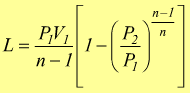
Analogalmente al caso della trasformazione adiabatica possiamo scrivere
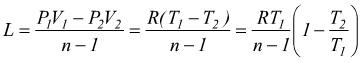 quindi
è anche
quindi
è anche
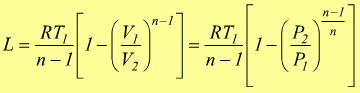
Il calcolo del calore scambiato è dato dal primo principio della termodinamica
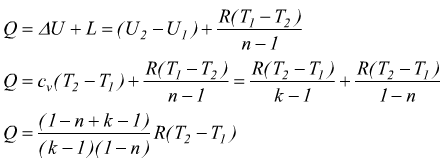
cioè:
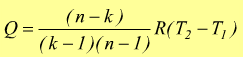
Secondo principio della termodinamica
Enunciato di Kelvin
Non è possibile realizzare una trasformazione il cui unico risultato sia quello di assorbire una quantità di calore da una unica sorgente termica e traformarla integralmente in lavoro.
Enunciato di Clausius
E' impossibile realizzare una trasformazione il cui unico risultato sia quello di far passare calore da un corpo freddo ad uno caldo.
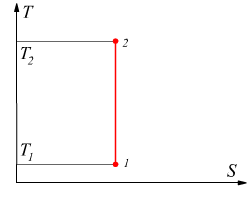
Nel primo enunciato (di Kelvin) si afferma che si devono disporre (almeno) di due sorgenti termiche, una a temperatura più alta T1 ed una a temperatura più bassa T2 (T1>T2) .
Maggiore è la differenza fra le due temperature, maggiore è il calore
che si può trasformare in lavoro.
Viene esclusa la possibilità di avere un'unica sogente termica
con la possibilità di convertire integralmente in lavoro il calore
rilasciato da questa sorgente.
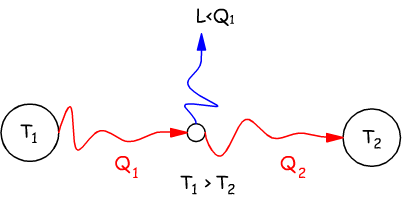
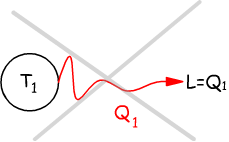
Solo una parte del calore Q1 ceduto dalla sorgente viene trasformato in lavoro; un'altra parte Q2 deve essere ceduta ad una sorgente a temperatura più bassa.
Ne deriva la definizione di rendimento termodinamico di una trasformazione:
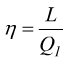 oppure
oppure 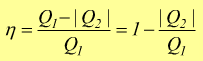
N.B.:il modulo |Q2| si impone perchè Q1 > 0 dato che si tratta di calore acquisito dal sistema (gas) mentre in generale è Q2 < 0 dato che si tratta di calore ceduto dal sistema all'ambiente.
Nell'enunciato di Clausius è implicita l'affermazione che il calore può spontaneamente passare solo da un corpo più caldo ad uno più freddo. Il processo inverso non è spontaneo, è possibile, ma richiede l'apporto di lavoro (macchine frigorifere).
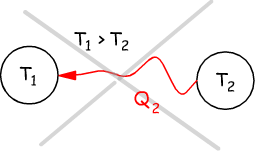
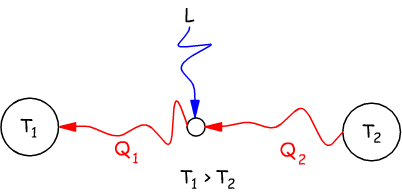
Gli enunciati di Clausius e di Kelvin esprimono con parole diverse (opposte) il secondo principio della termodinamica e in effetti, si nota, come i due schemi sono uno l'inverso dell'altro.
Legge di Dalton sulle pressioni parziali
Se consideriamo una miscela di gas, cioè più gas contenuti nello stesso recipiente, la pressione totale sarà data dalla somma delle pressioni parziali:
![]()
La pressione parziale di ciascun gas che fa parte di una miscela di gas (a comportamento ideale) è uguale alla pressione che quel gas eserciterebbe se occupasse da solo il volume occupato dalla miscela gassosa.
Gas reali
L'equazione di stato dei gas ideali viene formulata basandosi sull'ipotesi
che le molecole in fase gassosa occupino uno spazio trascurabile e che
non siano esercitate reciproche azioni attrattive o repulsive tra le
stesse.
Quando il gas soddisfa queste regole esso ha un comportamento
ideale.
A pressioni elevate, le molecole
di un gas sono costrette ad avvicinarsi tra loro, quindi la dimensione
della molecola non è più trascurabile rispetto alle distanze intermolecolari.
Alle basse temperature l'energia cinetica
delle molecole di gas diminuisce e il suo valore incomincia ad essere
paragonabile alle forze intermolecolari di natura elettrica che si instaurano.
Equazione di van der Waals
Uno studio dei gas reali che tiene conto dei volumi molecolari non nulli e della presenza di forze intermolecolari è stato condotto per la prima volta nel 1873 da J.D. van der Waals che riuscì a fornire una interpretazione del comportamenteo a livello molecolare dei gas reali attraverso a quella che comunemente viene chiamata l'equazione di van der Waals:
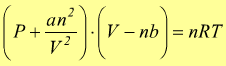
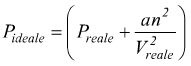 correzione
della pressione
correzione
della pressione
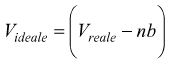 correzione
del volume
correzione
del volume
Pideale è la pressione esercitata dal gas in condizioni
ideali, cioè, se le forze intermolecolari fossero nulle.
Preale è la pressione effettivamente esercitata dal gas.
Vreale è il volume del contenitore.
Videale è il volume effettivamente a disposizione delle molecole.
Le costanti a e b per alcuni tipi di gas sono riportate nella seguente tabella
| Gas | a [atm·l2/mol2] | b [l/mol] |
| He | 0,034 | 0,0237 |
| Ne | 0,211 | 0,0171 |
| Ar | 1,34 | 0,0322 |
| Kr | 2,32 | 0,0398 |
| Xe | 4,19 | 0,051 |
| H2 | 0,244 | 0,0266 |
| N2 | 1,39 | 0,0391 |
| O2 | 1,36 | 0,0318 |
| Cl2 | 6,49 | 0,0562 |
| CO2 | 3,59 | 0,0427 |
| CH4 | 2,25 | 0,0428 |
| CCl4 | 20,4 | 0,138 |
| NH3 | 4,17 | 0,371 |
| H2O | 5,46 | 0,0305 |
A causa delle unità di misura in cui vengono espresse, quando si applica l'equazione di van der Waals è opportuno usare:
P pressione in [ atm ] (atmosfere)
V volume in [ l ] (litri)
T temperatura [K] (Kelvin)
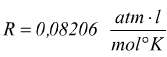 costante
universale di gas
costante
universale di gas
N.B.: il precedente valore di R può essere ricavato sapendo che a 0°C (273,15°K) e ad 1 atm una mole qualsiasi di gas ideale occupa un volume di 22,414 l ; eseguendo il calcolo
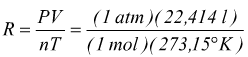
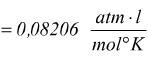
Esempio: un campione di 3 moli di ammoniaca gassosa occupa un volume V=0,005 m3 a 47°C calcola la pressione esercitata dal gas.
V=0,005m3=5dm3=5 l; 47°C=320 K
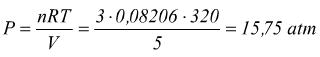 questa
è la pressione ideale
questa
è la pressione ideale
calcoliamo i termini correttivi per l'ammoniaca
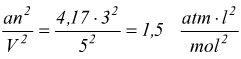
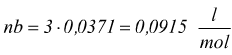

questa è la pressione osservata, effettivamente esercitata dal gas.
 edutecnica
edutecnica