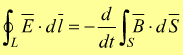Legge di Ampère-Maxwell
La legge di Faraday-Henry viene espressa dalla relazione
che lega la circuitazione del campo elettrico E, alla rapidità di variazione nel tempo del flusso del campo magnetico B, attraverso una superficie S che ha come contorno la linea chiusa L.
Per ragioni di simmetria ci si dovrebbe aspettare una espressione analoga che metta in correlazione la circuitazione di un campo magnetico con la rapidità di variazione di flusso del campo elettrico. L'unico indizio sembra essere l'equazione di Ampère per il campo magnetico:
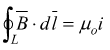
ma quest'ultima è valida in condizioni statiche e non contiene alcuna
variazione nel tempo del campo elettrico.
Nel 1873 Maxwell propose una modifica a questa equazione per renderla
adattabile anche a campi dipendenti dal tempo, introducendo il termine
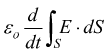corrente
di spostamento
ottenendo una relazione che descrive il comportamento dei campi elettrici e magnetici variabili:
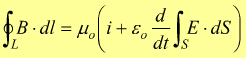legge
di Ampère-Maxwell
Questa equazione, nel caso di campi statici si riduce alla legge di
Ampère.
In essa si osserva come la presenza di un campo elettrico dipendente
dal tempo aggiunga alla corrente 'i' la corrente di spostamento indicata.
La legge di Ampère-Maxwell è dunque una estensione della legge di Ampère
e indica che anche un campo elettrico variabile nel tempo contribuisce
al campo magnetico; infatti in assenza di correnti si ha
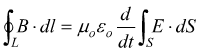
Cioè un campo elettrico dipendente dal tempo comporta l'esistenza di un campo magnetico tale che la circuitazione del campo magnetico lungo un percorso chiuso arbitrario sia proporzionale alla derivata rispetto al tempo del flusso del campo elettrico attraverso la superficie delimitata dal percorso stesso.
La corrente di spostamento è tutt'altro che una corrente ( lo stesso Maxwell usò questo termine in modo fittizio ) essa può più facilmente essere associata alla variazione nel tempo di un campo elettrico.
Come nel caso di un condensatore che si sta scaricando su un circuito
chiuso, il campo magnetico andrà a circoscrivere la corrente di conduzione
e questo avviene anche in prossimità del condensatore, solo che in quella
regione il conduttore non esiste e il circuito è aperto.
Quindi si può immaginare come prolungamento del conduttore il campo
elettrico variabile all'interno del condensatore. Al campo elettrico
variabile si associa una corrente di spostamento che genera un campo
magnetico variabile.
Considerando la legge dell'induzione elettromagnetica di Faraday-Henry per la quale ad ogni variazione di flusso concatenato ad un conduttore si induce in esso una f.e.m. viene da pensare ad una interpretazione più generale dell'induzione elettromagnetica non necessariamente vincolata ad all'esistenza di un conduttore fisico.
Se in un punto dello spazio è presente un campo magnetico variabile, si genera un campo elettrico variabile e viceversa, se è presente un campo elettrico variabile si genera un campo magnetico variabile.
Equazioni di Maxwell
L'interazione elettromagnetica è sempre in relazione ad una carica elettrica q in movimento che implica la presenza di un campo elettrico E ed un campo magnetico B che associate alla carica q determinano la forza meccanica
Forza
di Lorentz
Assieme a questa vi sono altre quattro leggi
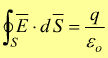Legge
di Gauss per il campo elettrico
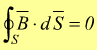Legge
di Gauss per il campo magnetico
La teoria del campo elettromagnetico è descritta da queste leggi, denominate
equazioni di Maxwell.
Anche se le leggi di Gauss per il campo elettrico e magnetico sono state
ottenute osservando campi statici, esse rimangono valide per campi variabili
nel tempo.
Le due leggi di Faraday-Henry e Ampère-Maxwell, definiscono, il legame
fra E e B che era assente nelle leggi per i campi statici.
Onde elettromagnetiche
Prima che Heinrich Hertz dimostrasse , nel 1890 che il campo elettromagnetico si propaga nel vuoto alla velocità della luce, Maxwell, analizzando le sue equazioni dimostrò teoricamente che i campi elettrico e magnetico soddisfano l'equazione delle onde
E' un'equazione lineare del secondo ordine alle derivate parziali che
descrive e sintetizza tutti
i fenomeni ondulatori,
essa è nota anche come equazione di D'Alembert o 'equazione della corda
vibrante'.
Abbiamo descritto un'onda progressiva viaggiante lungo la direzione
positiva x esprimendola come
essa è una soluzione particolare dell'equazione delle onde
infatti, deriviamo la precedente due volte rispetto al tempo :
poi la deriviamo due volte rispetto allo spazio x:
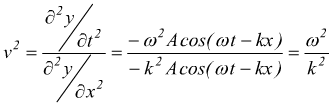
essendo ω=k·v l'equazione delle onde viene soddisfatta.
Le equazioni di Maxwell, applicate nel vuoto (e in assenza di cariche concorrenti) prevedono, infatti, come soluzione particolare un campo elettrico E ed un campo magnetico B perpendicolari fra loro che variano solamente lungo una direzione ortogonale ad ambedue.
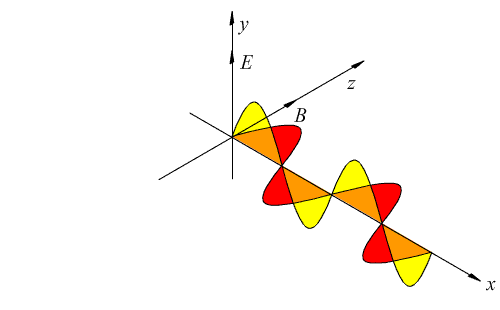
Sotto queste condizioni è possibile dimostrare che campo elettrico e magnetico soddisfano l'equazione delle onde:
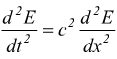
e
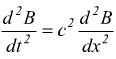
dove 'c' è la velocità della luce 3×108 m/s
Queste equazioni indicano che il campo elettrico E e il campo magnetico B si propagano lungo l'asse x con velocità c data da:
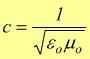
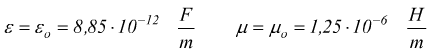
e possono essere espressi come
Infatti, nel caso delle equazioni di Maxwell si preferisce usare la grandezza campo magnetico H al posto del vettore induzione magnetica B. Nel vuoto:
Propagazione di onde elettromagnetiche
Nello studio delle onde si è visto come un'onda armonica progressiva che avanza in direzione positiva dell'asse x possa essere espressa come
con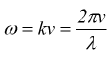 
quindi
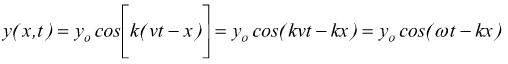
quindi per il solo campo elettrico possiamo dire
Un risultato analogo si ottiene per campo magnetico, si può infatti dimostrare che
il rapporto
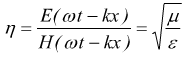viene
chiamato impedenza caratteristica del mezzo.
nel vuoto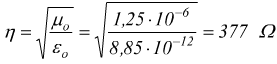 
nel caso le leggi di variazione del campo elettrico e magnetico siano di tipo armonico, le onde saranno sinusoidali, ma al posto della notazione trigonometrica può essere vantaggioso rappresentarle nella forma esponenziale
con EM=valore massimo del campo elettrico; ne consegue per il campo magnetico
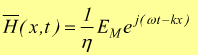tenendo
conto che
costante
di fase
( costante di fase o numero d'onda )
Si è detto che la velocità di propagazione di un'onda elettromagnetica
nel vuoto vale
se
non siamo nel vuoto dobbiamo usare 
con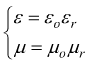 
con εr e μr rispettivamente costante dielettrica relativa e permeabilità magnetica relativa del mezzo trasmissivo in uso.
Energia di on'onda elettromagnetica
Il campo elettromagnetico,essendo costituito dall'insieme inseparabile
delle componenti E ed H, ha associato un'energia data dalla combinazione
di queste due.
Si può dimostrare che l'energia di un'onda elettromagnetica si propaga
sempre perpendicolarmente ai campi ai quali è associata,quindi lungo
la direzione della propagazione.
L'energia nell'unità di tempo che transita attraverso l'unità di superficie
normale alla direzione di propagazione è chiamata densità di potenza
S; nel vuoto:
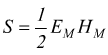considerando
la proporzione 
si ottiene 
densità
di potenza elettromagnetica.
Essendo, dimensionalmente, una potenza su unità di superficie, questa grandezza viene ottenuta dividendo la potenza emessa dal radiatore per la superficie del fronte d'onda. Quest'ultima è chiaramente funzione della distanza dalla sorgente.