Flusso magnetico
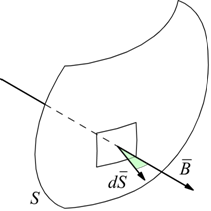
Formalmente, il flusso magnetico attraverso la superficie S, viene ottenuto eseguendo l'integrale (appunto) di superficie
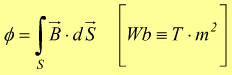
del prodotto scalare del vettore $B↖{→}$
campo magnetico, per $dS↖{→}$
che è un vettore rappresentativo della porzione infinitesima dS con
orientamento perpendicolare ad essa.
Semplificando al massimo, se il campo B fosse perpendicolare alla superficie
S, ipotizzata piana, il flusso sarebbe semplicemente $ϕ=B⋅S$.
Riguardo al magnetismo, si è detto, che non esistono poli magnetici isolati; le linee di forza del campo magnetico sono, dunque, sempre chiuse ( su un secondo polo ). Se si considera una superficie chiusa, posta in un campo magnetico, il flusso magnetico entrante è uguale al flusso magnetico uscente dato che lo stesso numero di linee di forza che entra all'interno della superficie deve anche uscirne. Si può quindi dire:
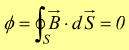 Il
flusso del campo magnetico attraverso una superficie chiusa è sempre
nullo.
Il
flusso del campo magnetico attraverso una superficie chiusa è sempre
nullo.
Questo risultato è noto come la legge di Gauss per il campo magnetico. Assieme alla legge di Gauss per il campo elettrico e la legge di Faraday-Henry vennero usate da J.K.Maxwell per definire compiutamente i fenomeni elettromagnetici.
Legge di Lenz
I campi elettrici e magnetici considerati precedentemente sono costanti ed invarianti nel tempo, per questo motivo essi sono chiamati campi statici. Il comportamento di campi dinamici viene descritto dalla legge di Lenz:
In un qualsiasi circuito chiuso posto in un campo magnetico variabile, viene indotta una forza elettromotrice uguale alla derivata rispetto al tempo del flusso magnetico attraverso il circuito cambiata di segno.
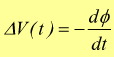
con ΔV(t) espressa in volt [V] mentre il flusso magnetico ϕ è espresso in weber [Wb].
Il segno meno che compare in questa espressione significa
che il verso della forza elettromotrice indotta è sempre tale da opporsi
alla variazione di flusso che la genera.
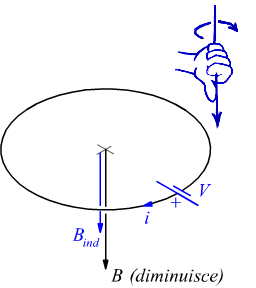
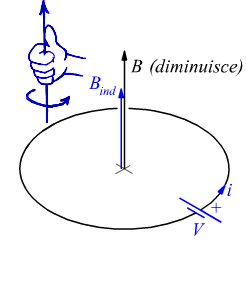
Ossia, se ϕ(B) diminuisce,
la f.e.m. indotta è tale che la corrispondente corrente circolante nel circuito,
genera un campo magnetico (indotto) che si aggiunge al campo magnetico inducente;
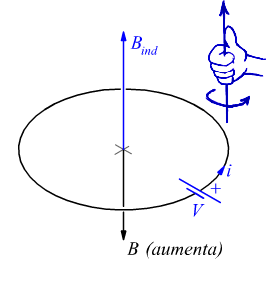
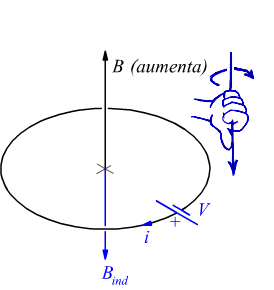
se ϕ(B) aumenta,
la corrente indotta ha il verso opposto e da luogo ad un campo magnetico
(indotto) che si sottrae al campo magnetico inducente.
Si nota che l'intensità della f.e.m. indotta dipende dalla rapidità della variazione di flusso magnetico; inoltre si intuisce come la variazione di flusso magnetico attraverso il circuito chiuso possa essere prodotto da un movimento relativo di quest'ultimo rispetto al campo.
Per valutare il senso in cui agisce la tensione indotta V, risulta estremamente utile la regola della mano destra: il pollice viene messo nella direzione e nel verso del campo magnetico e la f.e.m. agisce in senso opposto (uguale) a quello in cui sono orientate le dita quando il flusso aumenta (diminuisce).
Qui chiamiamo B il campo magnetico inducente
(applicato esternamente al circuito) e Bind
il campo magnetico indotto.
Notiamo come per trovare il verso della tensione indotta V bisogna applicare
la regola della mano destra al campo magnetico indotto Bind ,
tenendo conto che se il campo magnetico inducente B aumenta, Bind
si oppone ad esso mentre se il campo inducente B diminuisce Bind
si aggiunge ad esso.
La legge di Lenz è una diretta conseguenza (corollario) della legge di
Faraday-Henry .
Immaginiamo un conduttore elettrico che formi un circuito chiuso posto in
una regione interessata da un campo magnetico. Se il flusso magnetico attraverso
il circuito chiuso varia nel tempo, si osserva una corrente nel conduttore
mentre il flusso sta variando. La presenza di corrente indica la presenza
di un campo elettrico (E) nel conduttore, questo campo è causa della f.e.m.
indotta ΔV(t) . Formalmente la differenza di potenziale ΔV ed
il campo elettrico sono legate dalla relazione
 ma
è anche
ma
è anche 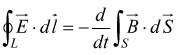
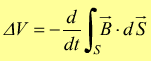 legge
di Faraday-Henry
legge
di Faraday-Henry
Quest'ultima scrittura significa: un campo magnetico dipendente dal tempo, comporta l'esistenza di un campo elettrico tale che la circuitazione del campo elettrico lungo un percorso chiuso arbitrario sia uguale ed opposta alla derivata rispetto al tempo del flusso del campo magnetico attraverso una superficie che ha per contorno quel percorso.
Conduttore in moto
Consideriamo il seguente sistema di conduttori
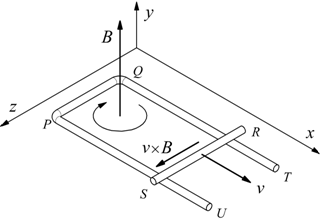
Il conduttore SR muove parallelamente a se stesso con velocità v mantenendo chiuso il contatto coi conduttori SP e QR. Il sistema SPQR forma un circuito chiuso attraversato dal campo magnetico B perpendicolare al piano del sistema. Sappiamo che su ogni carica q in moto in un campo magnetico grava una forza
$F↖{→}=qv↖{→}×B↖{→}$ ma il campo elettrico è espresso come $$E=F/q$$
$E↖{→}=v↖{→}×B↖{→}$ poi vedendo che v e B sono perpendicolari $E=vBsin90°=vB$ poniamo SR=l.
$$∫_{SPQR}B↖{→}⋅dS↖{→}=BS=Blx$$ derivando rispetto al tempo $${dϕ}/{dt}=Bl{dx}/{dt}=Blv$$
La legge di Faraday diventa in questo caso ![]()
con v=velocità del conduttore che sta tagliando le linee di
flusso magnetico.
Il comportamento del sistema, può dunque essere sommariamente
riassunto dal seguente schema:
Spira rotante
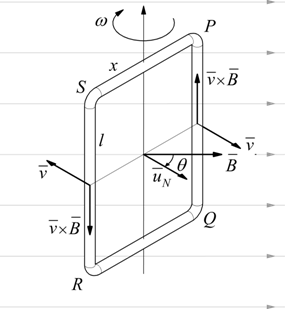
In questo caso, consideriamo un circuito rettangolare che ruota
in un campo magnetico uniforme B con velocità angolare
ω. Quando la normale uN al circuito
forma un angolo θ=ωt con il campo magnetico
B, tutti i punti di PQ si muovono con una velocità v
tale che il campo elettrico E=v×B è
rivolto da Q verso P e ha modulo E=vBsinθ.
In modo analogo per il tratto RS, la direzione di v×B
è quella da S a R ed il modulo è il medesimo.
Per quanto riguarda i lati RQ e PS, vediamo che v×B
è perpendicolare ad essi e che non esiste alcuna differenza
di potenziale fra S e P e fra R e Q.
Quindi se PQ = RS = l, la circuitazione del campo elettrico E lungo PQRS, cioè la f.e.m. applicata, è
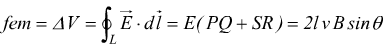
Se x = PS, il raggio della circonferenza descritta dalle cariche in PQ e SR è $$1/2x$$ quindi $$v=ω(x/2)=1/2ωx$$.
Poi si vede che S = l·x è l'area del circuito e vale la formula della velocità angolare $θ=ωt$, possiamo scrivere
![]()
Questa è la f.e.m. indotta, causata dalla rotazione del circuito nel
campo magnetico.
Il campo magnetico è uniforme ed il flusso che attraversa il circuito
vale:
$ϕ=BScosθ=BScos(ωt)$ se proviamo a derivare rispetto al tempo, otteniamo:
$$-{dϕ}/{dt}=ωBSsin(ωt)$$
La legge sull'induzione elettromagnetica è stata scoperta contemporaneamente nel 1830 da Michael Faraday e Joseph Henry che comunque vi arrivarono separatamente.
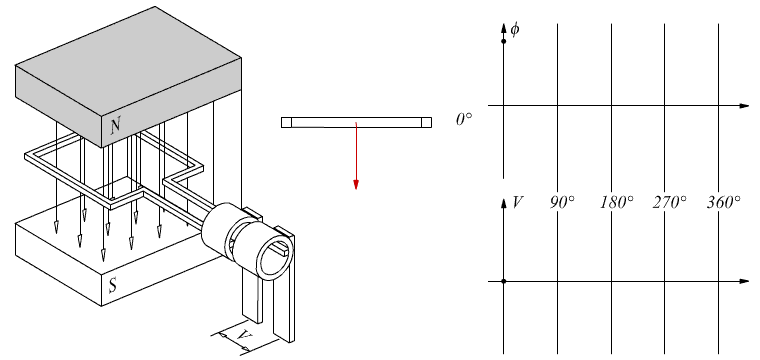
Nello schema disegnato il vettore verticale ( rosso ) è rappresentativo
del flusso magnetico concatenato alla spira.
Esso viene ottenuto dal prodotto scalare fra la normale alla superficie
della spira e il campo magnetico
( sempre verticale ).
Gli studi successivi sulla legge Faraday-Henry portarono alla fine del
diciannovesimo secolo alla costruzione del primo alternatore; un apparato
in grado di trasformare l'energia cinetica di una coppia meccanica in
energia elettrica successivamente impiegata, per usi domestici o industriali.
La ragione per la quale la tensione di alimentazione di rete venga prodotta
e distribuita sotto la forma alternata sinusoidale è dovuta al fatto
che essa viene ( quasi ) sempre generata da macchine rotanti.
 edutecnica
edutecnica