Onda piana

      

Consideriamo una funzione y=f(x) rappresentata dalla curva continua.
Se si sostituisce x con x-x_o con x_o > 0 si ottiene la funzione:

Questa funzione descrive la stessa curva precedente: gli stessi valori di y si trovano per valori di x aumentati di x_o.
Avendo ipotizzato x_o positivo si vede che la curva è stata spostata verso destra della distanza xo.
In modo analogo si nota come per y=f(x+x_o) la curva risulti traslata verso sinistra della distanza x_o.
Ora se x_o=vt con v=velocità e t=tempo si ottiene una curva 'in movimento'; cioè

rappresenta una curva che si muove verso destra con velocità v detta velocità di fase. in modo analogo una funzione del tipo y=f(x+vt) rappresenta una curva che si sposta verso sinistra con la velocità v.
Si conclude che la forma matematica

è adatta a descrivere una perturbazione fisica che si propaga senza deformazione, lungo la direzione positiva o negativa dell'asse x, l'unico difetto è che ha, è si tratta di una funzione a due variabili.

Onda armonica

      

Un caso interessante è quanto la funzione y(x,t) è una funzione sinusoidale ( o armonica )

     e ricordandosi che          si può riscrivere come

            più in generale si stabilisce che

      viaggia in direzione positiva della x

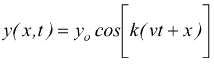       viaggia in direzione negativa della x

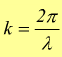      numero d'onda

     lunghezza d'onda

La lunghezza d'onda è il periodo 'spaziale' della curva: la curva ripete se stessa ogni lunghezza λ. Sostituendo

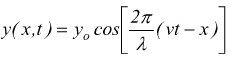                  le relazioni precedenti possono anche essere espresse come

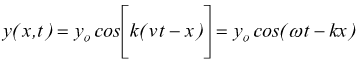
con         frequenza angolare ( o pulsazione )

dal moto armonico è noto che la frequenza angolare ( o velocità angolare )

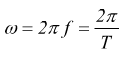     quindi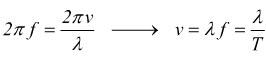     

T=periodo:intervallo di tempo impiegato dalla curva per effettuare un'oscillazione completa.
f=frequenza: numero di oscillazioni effettuate nell'unità di tempo.
riprendendo le relazioni precedenti si ha

   o anche

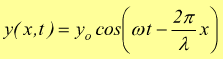       onda progressiva ( direz.positiva x )

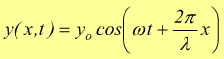       onda regressiva ( direz.negativa x )

Dalla relazione della velocità si è visto che è        

che indica che la lunghezza d'onda è la distanza percorsa dall'onda in un periodo.

Si conclude che nel moto ondulatorio sinusoidale ( moto armonico ) si hanno due periodicità una legata al tempo data dal periodo T e una riferita allo spazio data dalla lunghezza d'onda λ. Le due periodicità possono anche essere considerate separatamente, infatti l'equazione generale per un onda piana progressiva per t=0 restituisce una 'fotografia' spaziale dell'onda in quell'istante.

      

mentre per x=0 si ha una rappresentazione temporale dell'oscillazione

                 

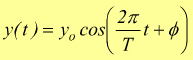
con φ=fase iniziale, cioè il valore iniziale dell'onda.
Se φ=0 la sinusoide parte dal suo valore massimo di picco, ma questo deve essere specificato caso per caso.

Interferenza

      

I fenomeni di interferenza fra onde, sono regolati dal principio di sovrapposizione:

Due o più onde che si propagano nello stesso mezzo, generano una perturbazione che è la somma algebrica delle perturbazioni che ciascuna onda produrrebbe da sola.

Abbiamo qualificato un'onda progressiva come

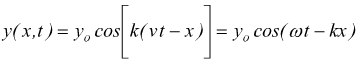
L'ipotesi di studio più semplice sarebbe quella di due onde che abbiano la stessa ampiezza, la stessa velocità e la stessa direzione di propagazione ( ambedue progressive ), sfalsate fra loro di una fase φ.

per le formule di prostaferesi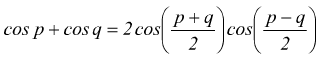       

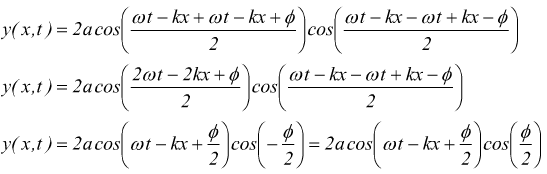
studiando quest'onda in un punto scelto arbitrariamente, ad es. x=0

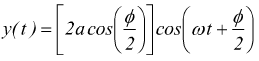
viene ottenuta un'altra onda armonica composizione delle due onde armoniche sommate che ha la stessa pulsazione e quindi la stessa frequenza delle sue due componenti con fase iniziale pari a φ/2 e con ampiezza.

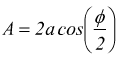       l'ampiezza dell'onda dipende dallo sfasamento φ.

Se invece pensassimo di far entrare in interferenza due onde con direzione di propagazione opposta, ma che abbiano comunque la stessa velocità, la stessa pulsazione e la stessa lunghezza d'onda, dovremmo scrivere:

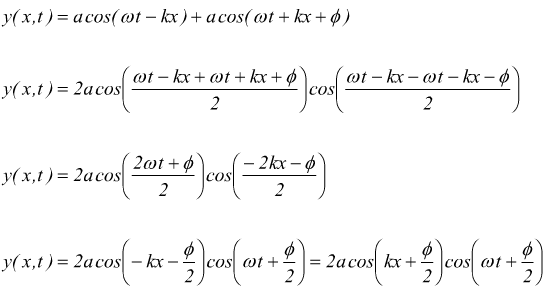
anche in questo caso in x=0 si avrebbe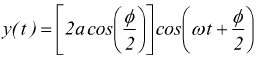                

Riflessione

      

Un fenomeno che può essere osservato è il comportamento di un'onda in corrispondenza di un ostacolo o di un limite del mezzo fisico lungo il quale essa si muove.

Prendiamo ad esempio una perturbazione che si propaga lungo una corda sotto forma di onda trasversale; se per ipotesi la corda è vincolata ad un suo estremo, l'impulso che si propaga viene riflesso contro l'ostacolo ed esso torna indietro capovolto.

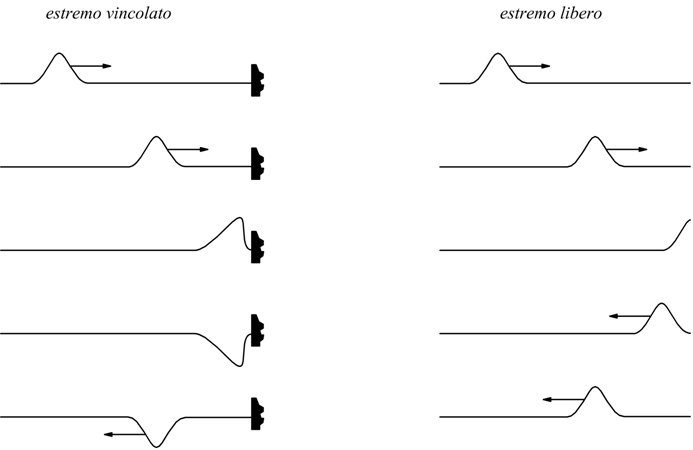
Nel caso l'estremo finale della corda sia libero e non vincolato, l'onda viene ugualmente riflessa ma non vi è alcun capovolgimento, la perturbazione torna a propagarsi all'indietro senza alcuna inversione della sua ampiezza.

Bisogna tener conto di questi dettagli quando si cerca di studiare il moto di onde su mezzi fisici di dimensione limitata.

Onda stazionaria

      

Un onda stazionaria è un onda che si muove in una zona limitata di spazio e non ha modo di propagarsi.
Esempi tipici di onda stazionaria sono la vibrazione della corda di una chitarra (onda trasversale) oppure le oscillazioni del moto sulla superficie di un fluido in un contenitore ( onda longitudinale ).
Si può osservare come la generazione di un'onda stazionaria riconducibile ad un onda che si propaga su un mezzo e raggiunti il limiti spaziali di questo mezzo inizi ad entrare in interferenza con se stessa per effetto dell'onda riflessa generata dalla collisione col contorno del mezzo.
Possiamo ottenere la descrizione matematica di un'onda stazionaria come nel caso precedente, facendo però attenzione al fatto vi è differenza di fase fra l'onda diretta e quella riflessa di π=180° nel caso di estremo vincolato verso il quale l'onda collide.
Qui sotto, si osserva la costruzione di un'onda stazionaria, evidenziando la posizione dei vari nodi ed antinodi ( ventri ).

Quindi le due onde che vanno in interferenza ( si sommano ) sono:

      onda diretta progressiva

      onda riflessa, regressiva, invertita di 180°

Le due onde hanno la stessa velocità

applicando la formule di prostaferesi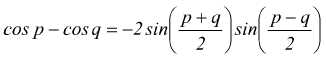     

ricordando che

E' un'onda oscillante al passare del tempo ma non è progressiva ne regressiva.
La sua ampiezza non è costante; per un generico punto x essa ha ampiezza massima :

   in tal punto l'onda oscilla fra i valori estremi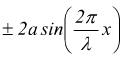

In particolare nel punto x=0 l'ampiezza è nulla; lo stesso deve accadere all'estremo opposto del campo di variabilità di x che chiamiamo L (condizioni al contorno). Si deve dunque verificare:

      

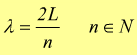
L'onda stazionaria può oscillare soltanto in determinati modi denominati modi normali.
Il numero dei modi normali di oscillazione è uguale al numero dei punti x in cui l'ampiezza dell'onda si annulla.
L'equazione dell'onda stazionaria deve dunque essere corretta formalmente sostituendo il valore di λ nell'eq. precedente:

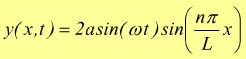
L'individuazione dei punti x in cui l'ampiezza dell'onda si annulla possono allora essere ottenuti imponendo:

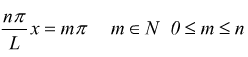     cioè             sotto queste condizioni:

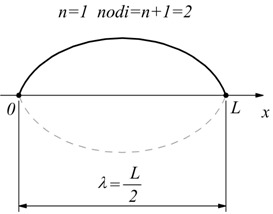       Se n=1 si ha: m=0 o m=1

      Se n=2 si ha: m=0 o m=1 o m=2

     Se n=3 si ha: m=0 o m=1 o m=2 o m=3

e così via...

 

Un'onda stazionaria sarà caratterizzata da un certo numero di nodi=n+1 sempre fissi in cui l'ampiezza dell'onda è nulla.

Combinando la    e la

       

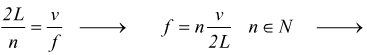
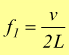
Le frequenze di tutti i modi normali di oscillazione saranno multipli di una frequenza f₁ chiamata frequenza fondamentale o prima armonica.

Velocità di gruppo

      

Come si è visto, le onde stazionarie sono sostanzialmente delle onde con la stessa frequenza, la stessa ampiezza (opposta) la stessa velocità ( opposta ) che entrano in interferenza fra loro; ma la generazione e la trasmissione di segnali sonori o elettromagnetici comporta delle caratteristiche più complesse nella combinazione di più segnali elementari.

Ipotizziamo due sinusoidi di frequenze e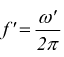   

con f ed f' molto vicine fra loro. Sommando queste due onde progressive si ha:

applicando la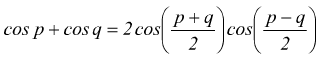

    [#]

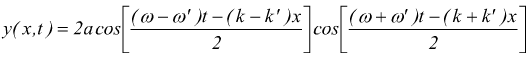localizzata per x=0

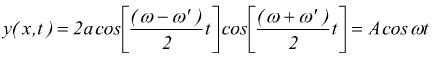
L'onda risultante è un'onda periodica con ampiezza

      variabile nel tempo e pulsazione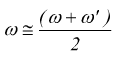

teoricamente si tratterebbe della media aritmetica delle pulsazioni delle due componenti.
Se anche le velocità delle due onde sono molto prossime fra loro:

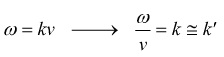
quindi, l'espressione completa di questo segnale [#] può essere così approssimata

Si deduce che l'onda risultante è in movimento con una velocità

             velocità di gruppo

quindi è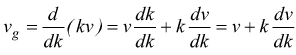

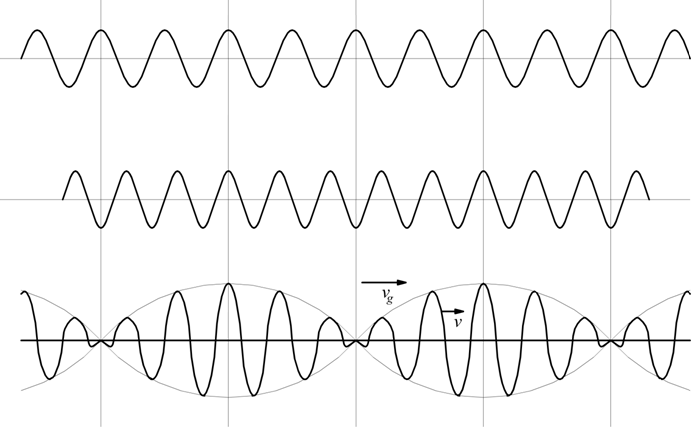
Questo fenomeno, noto col nome di battimenti, è caratteristico di quando si combinano due onde sonore con le caratteristiche suddette, generando un unico suono che ha la frequenza uguale alla media delle due frequenze ed intensità variabile nel tempo.