Legge di Coulomb
La grandezza fisica responsabile dei fenomeni elettrici è la carica elettrica.
Essa viene indicata con la lettera Q e la sua unità di misura è il Coulomb
[C].
La carica elettrica ha una natura duale, nel senso che esistono due tipi
di elettricità: l'elettricità positiva e l'elettricità negativa.
Due corpi elettricamente carichi si respingono se dotati di carica omonima
( entrambi di carica positiva o entrambi dotati di carica negativa ) si
attraggono se dotati di carica eteronima ( di segno diverso ).
Non tutti i materiali hanno la peculiarità di caricarsi elettricamente
o di condurre efficacemente l'elettricità, esistono infatti, materiali
nei quali la carica elettrica fluisce con facilità ed essi vengono chiamati
conduttori.
Altri materiali non lasciano sfuggire le cariche elettriche ed essi vengono
definiti come isolanti.
In generale, un corpo che conduce bene l'elettricità è anche un buon conduttore
di calore. Viceversa un pessimo conduttore di elettricità e anche un cattivo
conduttore di calore.
Tutti i materiali metallici sono buoni conduttori.
Le plastiche, il vetro, la ceramica, sono isolanti.
Chiaramente l'elettricità ha a che fare con la capacità che hanno gli
elettroni che orbitano attorno ai vari atomi di un materiale, a trasferirsi,
qualora le condizioni lo permettano, da una regione all'altra dello spazio.
Per questa ragione non è mai stata osservata una carica elettrica di quantità
minore alla carica dell'elettrone e=1,6·10-19 C, si
dice quindi, che la carica elettrica ha un carattere granulare ( è quantizzata)
ogni quantità è un multiplo intero della carica dell'elettrone 'e'.
Abbiamo detto che due corpi carichi entrambi positivamente o negativamente
si respingono e che invece, due corpi dotati di carica di segno diverso
si attraggono; il fenomeno elettrico si manifesta attraverso una forza
meccanica. La formulazione della relazione tra questa forza meccanica
e le cariche elettriche che la generano viene descritta dalla legge di
Coulomb (1784).
La legge di Coulomb afferma che la forza di attrazione o di repulsione, che si esercita tra due corpi puntiformi elettrizzati, è direttamente proporzionale al prodotto delle quantità di elettricità possedute da due corpi e inversamente proporzionale al quadrato della loro distanza.
Se si indicano con Fo l'intensità della forza ( attrattiva o repulsiva ) che ciascuno dei due corpi esercita sull'altro nel vuoto, con Q e q le loro cariche elettriche e con r la loro distanza, la legge di Coulomb si scrive:
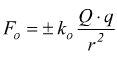 con
con 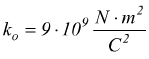
dove ko è un coefficiente di proporzionalità che per definizione è
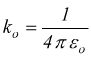 εo=costante
dielettrica del vuoto
εo=costante
dielettrica del vuoto 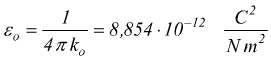
ko=9·10-9 N·m2/C2
q1
q2
r
F [N]
se l'ambiente non è il vuoto, ma uno specifico materiale, bisogna considerare
la costante dielettrica relativa εr di quel
materiale per definire.
![]() per
cui
per
cui 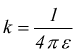 la
legge di Coulomb diventa
la
legge di Coulomb diventa
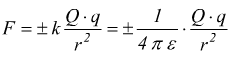
La direzione della forza F è quella della retta che congiunge i due corpi
carichi. Come si vede dalla formula, l'intensità della forza diminuisce
rapidamente (col quadrato della distanza) all'aumentare della loro distanza:
si riduce a un quarto, a un nono..etc.
La forza espressa è repulsiva per cariche omonime (dello stesso segno)
, attrattiva per cariche eteronime (di segno diverso).
| Materiale (T=298°K) |
Costante dielettrica
relativa |
| Ambra | 2,8 |
| Carta | 2,1 |
| Legno | 3÷7 |
| PVC | 4,5 |
| Silicio | 12 |
| Vetro | 5÷10 |
| Zucchero | 3,3 |
| Alcol etilico | 24÷26 |
| Ghiaccio | 75 |
| Acqua | 80 |
| Vapore acqueo | 1,00060 |
| aria | 1,00056 |
Campo elettrico
Come nel caso della forza di attrazione gravitazionale, si può pensare
che la presenza di una carica elettrica vada a modificare le caratteristiche
dello spazio che la circonda.
Per la legge di gravitazione, la presenza di una massa implica la creazione
di un campo gravitazionale che interessa
la zona circostante la massa, per l'elettricità la presenza di una carica
in una certa regione dello spazio comporta l'attuazione istantanea di
un campo elettrico: in tutti e due i
casi si tratta di una forza che agisce a distanza; l'unica differenza
è che il campo elettrico è duale ( la forza può essere attrattiva o repulsiva
) il campo gravitazionale non lo è ( l'interazione fra due masse può essere
solo attrattiva ).
Per la carica elettrica viene, dunque, definito il vettore campo elettrico come:
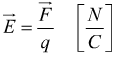 ovviamente è anche
ovviamente è anche
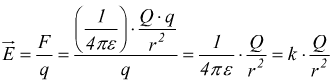
mentre nel vuoto si ha 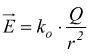
Viene definito campo elettrico una qualsiasi regione
dello spazio in cui una carica elettrica sia soggetta all'azione di una
forza.
La forza è causata dalla presenza di altre cariche elettriche nella regione
interessata dal fenomeno.
Essendo la legge di Coulomb, formalmente identica alla legge di gravitazione universale. è facile realizzare il seguente parallelismo
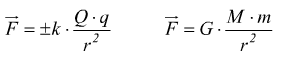
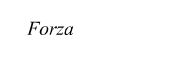
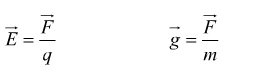

![]()
![]()
Il campo generato da più di una carica, ad esempio dalle due cariche Q1 e Q2 è necessariamente la composizione vettoriale dei campi generati dalle due cariche.
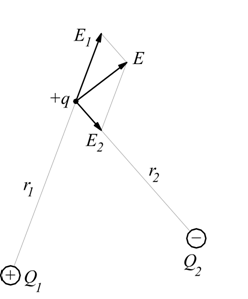
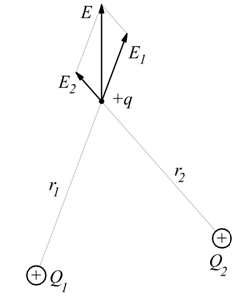
Ipotizzando come carica di prova un protone ( carica positiva ). Si hanno delle varianti a secondo dell'intensità e del segno delle cariche circostanti come riportano nel seguente demo.
Dato che le forze a cui è soggetta la carica campione q sono:
![]() con
il vettore campo
con
il vettore campo
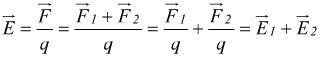
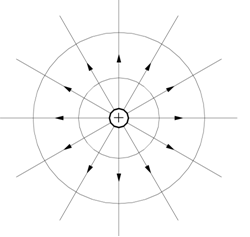
Come nel caso del campo gravitazionale, un campo elettrico può essere
rappresentato da linee di forza . Queste
linee sono disegnate in modo da essere tangenti in ogni punto alla direzione
del campo elettrico in quel punto.
Un campo elettrico uniforme ha
dappertutto la stessa intensità e direzione di conseguenza un campo
elettrico uniforme è rappresentato da linee di forza parallele.
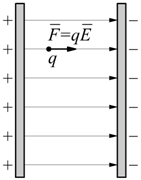
Un metodo classico per realizzare un campo elettrico uniforme è
quello di caricare due lastre metalliche parallele con cariche uguali
ma di segno opposto
Campo elettrico di una carica puntiforme
Riscriviamo la legge di Coulomb ( nel vuoto )nella seguente forma
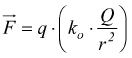
esprime la forza esercitata dalla carica Q sulla carica q posta a distanza r da Q, se volessimo usare la relazione del campo dobbiamo assumere
 in
modulo, mentre in forma vettoriale:
in
modulo, mentre in forma vettoriale:
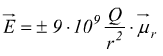
con versore ![]() in direzione radiale uscente rispetto la carica Q se
questa è positiva, entrante se negativa.
in direzione radiale uscente rispetto la carica Q se
questa è positiva, entrante se negativa.

Potenziale elettrico
Si è accennato prima che il campo elettrico è caratterizzato da una energia potenziale
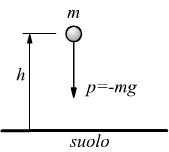 Nel campo gravitazionale per portare una massa m dal suolo ad una altezza
h, è necessario usare una forza esterna -p uguale e contraria al peso
capace di compiere il lavoro
Nel campo gravitazionale per portare una massa m dal suolo ad una altezza
h, è necessario usare una forza esterna -p uguale e contraria al peso
capace di compiere il lavoro
![]()
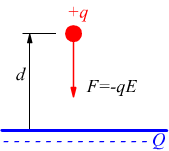 Nel
campo elettrico per portare la carica di prova q ad una distanza d dalla
carica fissa Q è necessario l'intervento di una forza -F uguale e contraria
alla forza del campo e capace di fare un lavoro
Nel
campo elettrico per portare la carica di prova q ad una distanza d dalla
carica fissa Q è necessario l'intervento di una forza -F uguale e contraria
alla forza del campo e capace di fare un lavoro
![]()
In entrambi i casi il lavoro compiuto dalla
forza esterna viene immagazzinata dal corpo sotto forma di energia potenziale
U quindi
U=mgh per il campo
gravitazionale
U=qEd per
il campo elettrico
La particella, possiede una energia potenziale perché il campo compie
un lavoro quando sposta la particella da una posizione ad un'altra percorrendo
la distanza d.
Il potenziale elettrico
in un punto del campo è definito come il rapporto fra l'energia potenziale
e la carica della particella in quel punto:
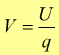 l'unità di misura è J/C=V [volt]
l'unità di misura è J/C=V [volt]
Si nota come sia anche 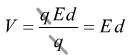 in
termini vettoriali
in
termini vettoriali
![]() questa
formula è la relazione fra potenziale e campo.
questa
formula è la relazione fra potenziale e campo.
Per questo motivo, il campo può essere espresso come [ V/m ] (volt su metro).
Il potenziale può essere dunque interpretato come il lavoro svolto dal campo E per spostare la carica q di uno spostamento d.
sappiamo che il meccanica il lavoro viene definito come forza×spostamento
![]() mentre
il campo elettrico è definito come
mentre
il campo elettrico è definito come
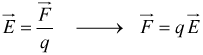 sostituendo
questa forza F nell'equazione del lavoro
sostituendo
questa forza F nell'equazione del lavoro
![]()
![]()
Il lavoro compiuto dalla forza elettrica F per portare la carica q dal
punto 1 al punto 2 è uguale al prodotto fra il valore della carica e
la differenza di potenziale fra i due punti.
Si vede come per una carica di valore unitario
q=1C il lavoro compiuto da F coincide con la differenza di potenziale
fra la posizione finale e quella iniziale.
Val la pena riassumere
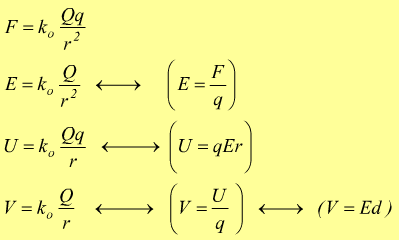
Quando si tiene conto della massa delle cariche in movimento non bisogna dimenticarsi della legge di Newton F=ma. Per gli spostamenti diretti secondo le linee del campo si ha la relazione:
![]()
Forza elettromotrice
Pensiamo ad una carica unitaria q=1C in un campo E: il lavoro compiuto per spostare questa carica lungo il generico percorso l è dato da
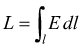 ma
questo lavoro può essere espresso in volt perché coincide con L/q.
ma
questo lavoro può essere espresso in volt perché coincide con L/q.
Si è visto come per un campo elettrostatico la differenza di potenziale fra due punti è uguale al lavoro compiuto dal campo elettrico per spostare la carica unitaria:
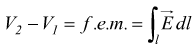
Questa differenza di potenziale viene anche chiamata forza elettromotrice (f.e.m.). Il percorso l è arbitrario quindi sei il il punto finale 2 e quello iniziale 1 coincidono cioè se il percorso scelto è un percorso chiuso si ha:
![]()
e l'integrale di linea si esprime come integrale ciclico
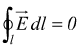 lavoro
compiuto lungo un percorso chiuso
lavoro
compiuto lungo un percorso chiuso
Un tale integrale viene chiamato circuitazione.
Nel campo elettrostatico, il lavoro compiuto
nello spostare una carica lungo un percorso chiuso
( circuitazione ) è sempre nullo.
Questa proprietà (presente anche nel campo gravitazionale) qualifica il campo elettrico come campo di tipo conservativo e le forze elettrostatiche come forze conservative.
Flusso di un campo elettrostatico
Prendiamo una superficie piana di area S attraversata da un campo E uniforme.
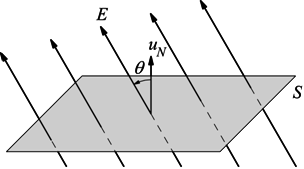
Se la normale alla superficie forma un angolo θ con la direzione del campo, definiamo il flusso elettrico come la quantità scalare
![]()
Se la superficie è perpendicolare al campo θ=0 → cosθ=1 il flusso è massimo; se la superficie è parallela al campo θ=90° → cosθ=0 il flusso è nullo.
Se la superficie e/o il campo non è uniforme si divide la superficie i tanti elementi dS1 dS2…dSn arbitrariamente piccoli, per ciascuno definianiamo un versore unitario u1 u2..un normale alla superficie in quel punto, pertanto
![]()
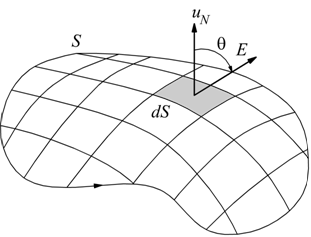
con i vettori campo elettrico
![]()
inclinati con angoli
![]()
verso le rispettive superfici si ha
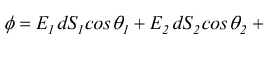
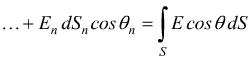
cioè bisogna fare un integrale di superficie.
E' importante osservare che l'argomento dell'integrale
è il prodotto scalare
![]()
Con ![]() che ha direzione
normale all'elemento di superficie considerato.
che ha direzione
normale all'elemento di superficie considerato.
Qui maggiori
informazioni sull'integrale di superficie.
Se la superficie è chiusa, come nel caso di una sfera, con i versori
sempre normali alla superficie, si usa la notazione:
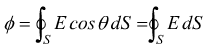 Il
flusso è positivo se uscente.
Il
flusso è positivo se uscente.
Legge di Gauss per il campo elettrico
Consideriamo il campo elettrico generato da una carica puntiforme che come visto prima vale
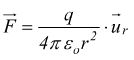
Il versore normale alla superficie di una sfera concentrica rispetto
la particella, coincide con il versore lungo la direzione radiale
ur.
L'angolo θ fra il campo elettrico E ed il versore normale
ur è zero, quindi cosθ=1 sempre.
Il campo ha lo stesso modulo in tutti i punti della superficie sferica,
si ha
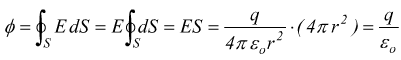
si trova che il flusso elettrico è indipendente dalla superficie.
Quindi, in generale se una carica q si trova all'interno di una superficie
chiusa il suo flusso è costante e vale q/εo. Se invece
la carica si trova all'esterno della superficie chiusa il flusso elettrico
attraverso la superficie è nullo. Questo è il teorema di Gauss sul campo
elettrico:
Il flusso elettrico attraverso una superficie chiusa che circonda le cariche q1 q2 q3..è:
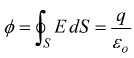 con
con ![]()
carica totale contenuta all'interno della superficie chiusa.
Campo elettrico generato da una distribuzione piana
La legge di Gauss torna utile quando vogliamo calcolare il campo elettrico prodotto da distribuzioni di carica che hanno determinate simmetrie geometriche.
E' il caso di una carica distribuita uniformemente su di un piano con
densità di carica 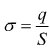

Le
linee di flusso sono ortogonali al piano e se la carica è positiva esse
sono uscenti da esso.
Scegliendo come superficie chiusa il cilindro indicato, si vede come
il flusso totale emesso dal piano è dato dal flusso uscente da S1
che vale +E·S e dal flusso uscente attraverso S2 che
vale anche lui +E·S.
Notiamo, infatti, come in tutti i possibili
elementi di superficie laterale i due vettori E e dS sono ortogonali,
quindi il loro prodotto scalare è zero. Il flusso uscente
è dato solo dal contributo del campo per le superfici trasversali
del cilindro.
Quindi il flusso totale uscente vale 2ES; dalla legge di Gauss
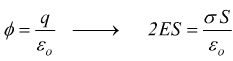 quindi
quindi 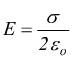
Campo elettrico fra due superfici piane parallele
Nel caso di due piani paralleli con cariche uguali ma segni opposti. Si nota come nello spazio esterno ai due piani vi sono campi elettrici uguali in modulo ma di verso opposto che danno luogo ad un campo risultante nullo. Nella zona compresa fra i due piani , i campi hanno lo stesso verso e il campo risultante è il doppio del valore dal campo prodotto da un singolo piano si avrà dunque:
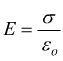
Se d è la distanza compresa fra i due piani, la differenza di potenziale vale
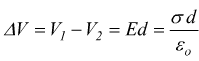
Campo elettrico generato da una carica sferica
Considerando una sfera di raggio a e carica q si nota che per simmetria il campo sia in ogni punto radiale e dipenda solo dalla distanza r del punto in analisi rispetto al centro della sfera. Si traccia una generica superficie S di raggio r concentrica alla sfera carica e si trova il flusso elettrico che la attraversa
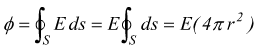
se r > a tutta la carica è contenuta dentro la superficie S; quindi applichiamo la legge di Gauss
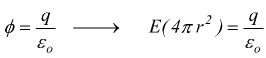 si
ha
si
ha 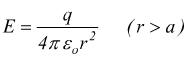
che poi è lo stesso risultato che si è avuto nel caso della carica puntiforme.
Si può dire, dunque, che il campo al di fuori di una sfera carica è lo
stesso che si avrebbe se tutta la carica fosse concentrata nel suo centro.
Considerando il caso r < a bisogna distinguere.
Se la carica si trova solo sulla superficie della sfera la carica totale
interna alla superficie S' concentrica alla sfera è zero quindi
per la legge di Gauss E=0.
Se invece pensiamo che la sfera sia carica uniformemente su tutto il suo volume chiamiamo q' la carica interna alla superficie S' concentrica ed interna alla sfera.
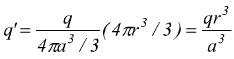 per
cui, la legge di Gauss fornisce la soluzione
per
cui, la legge di Gauss fornisce la soluzione

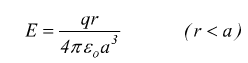
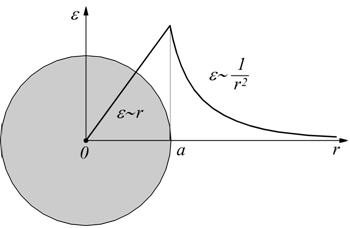
Il campo elettrico in un punto interno ad una sfera uniformemente carica in tutto il suo volume è direttamente proporzionale alla distanza del punto considerato dal centro della sfera.
Campo elettrico generato da un cilindro
Ipotizziamo un cilindro di lunghezza L di raggio a con λ la carica per unità di lunghezza, quindi con q=λ·L. Si intuisce come il campo elettrico dipende solo dalla distanza del punto dall'asse del cilindro ed è sempre diretto radialmente. Ipotizziamo una superficie S di raggio r > a il flusso emesso lateralmente è
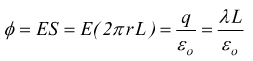
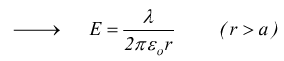
in questo caso il campo è inversamente proporzionale alla distanza r.
Notiamo come in questa formula il campo sia indipendente dal raggio del
cilindro, quindi essa può essere usata anche nel caso di un filo ( unidimensionale
) del quale sia nota λ.
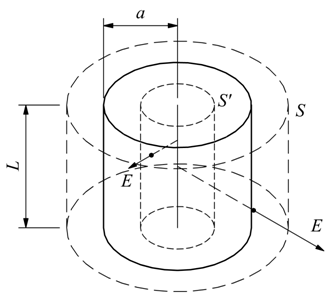
Nel caso si abbia r < a anche in questo caso, se la carica è distribuita solo sulla superficie del cilindro, internamente ad esso non si ha carica, allora per la legge di Gauss si ha E=0.
Se invece la carica è distribuita uniformemente nel volume del cilindro, si deve prima trovare la carica q' contenuta internamente alla superficie S' di raggio r
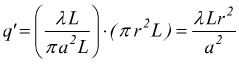 poi
si applica la legge di Gauss
poi
si applica la legge di Gauss
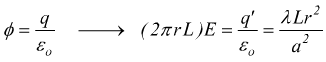 e
si trova infine
e
si trova infine
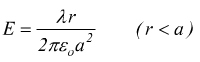
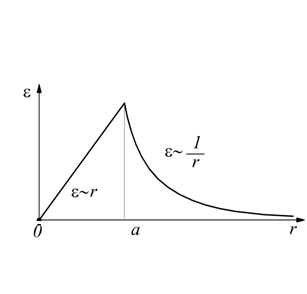
in questo caso il campo è direttamente proporzionale alla distanza r.
 edutecnica
edutecnica