Altre teorie sulla probabilità

                 

Oltre alla teoria classica di probabilità elaborata dal grande matematico francese Laplace nelle sue opere «Theorie analytique des probabilités» del (1812) e «Essai philosophique sur les probabilités» del (1819) ne sono state sviluppate altre nel corso del tempo

• Teoria frequentistica della probabilità.
• Teoria soggettivista della probabilità.
• Teoria assiomatica della probabilità.
• Assiomi del calcolo della probabilità.

In questa pagina abbiamo voluto fare un piccolo approfondimento circa queste teorie e le loro definizioni.

Teoria frequentistica della probabilità

                 

La constatazione che la probabilità teorica di diversi eventi riguardanti la realtà nel suo complesso (eventi meteorologici, sociali, economici, ecc.) non si può calcolare, in quanto i casi possibili non si conoscono, oppure non sono equiprobabili, ha portato alla nascita della teoria frequentista della probabilità.

Essa nasce nel 1800 e si fonda su prove sperimentali effettivamente svolte, riguardo all’evento considerato.

Per fissare le idee, facciamo il seguente esempio: dato un cilindretto di plastica infrangibile, vogliamo sapere la probabilità che esso, lasciato cadere liberamente da una certa altezza, finisca per arrestarsi sul pavimento in posizione verticale, con la base A in alto.

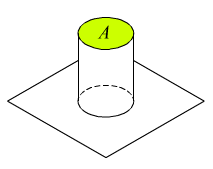
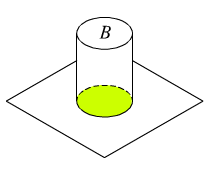
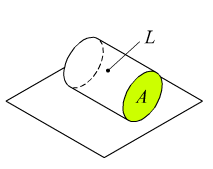
Per sintetizzare, diciamo che si vuole determinare la probabilità dell’evento:
E = «Esce la base A»
I casi possibili sono rappresentati dai tre eventi elementari seguenti:
e₁ = «Esce la base A»
e₂ = «Esce la superficie laterale L»
e₃ = «Esce la base B»

Si capisce subito che questi tre casi possibili non sono equiprobabili: infatti, l'esperienza insegna che l'evento e₂ si realizza più facilmente degli altri due eventi elementari.

Quindi, pur conoscendo il numero dei casi possibili (n = 3) e quello dei casi favorevoli (m = 1), sarebbe un grave errore affermare che:

$$p(E)=m/n=1/3$$

in quanto, come sappiamo, la probabilità a priori di un evento casuale si può calcolare solo quando i casi possibili hanno tutti la stessa probabilità di realizzarsi.

Non potendo quindi calcolare la probabilità teorica dell’evento E, si segue un’altra via, questa volta di tipo sperimentale. Essa consiste nell’eseguire effettivamente un gran numero di prove, svolte tutte nelle stesse condizioni; ad esempio, si potrebbe effettuare ciascuna prova lasciando cadere liberamente il cilindretto da una altezza di due metri e osservando l’esito cosi ottenuto.

Facciamo l’ipotesi che, nel corso di n = 100 prove, l’evento E = «Esce la base 4» si sia verificato 7 volte. In tal caso, si dice che la frequenza relativa (relativa al numero di prove effettuate) dell’evento E è la seguente:

$$f(E)=k/n=7/100=0,07$$

Secondo l'impostazione frequentista, la frequenza relativa dell’evento E, ottenuta dopo un gran numero di prove svolte nelle stesse condizioni, si assume come valore approssimato della probabilità dello stesso evento casuale.
Quindi, si può scrivere:

$p(E)≃f(E)=0,07$

L’esperienza indica che, in generale, il grado di approssimazione della probabilità migliora se si aumenta il numero delle prove. Per fissare le idee, se supponiamo di eseguire n = 1000 prove e che, nel corso di queste, I'evento E si sia verificato k = 73 volte, allora la nuova frequenza relativa risulta:

$$f(E)=k/n=73/1000=0,073$$

e quindi potremo scrivere che:

$p(E)≃f(E)=0,073$

Questo valore, in generale, rappresenta una stima più attendibile della probabilità dell’evento E, essendo molto più elevato il numero delle prove eseguite. Aumentando ulteriormente il numero n delle prove, si osserva che la frequenza relativa di E tende a stabilizzarsi intorno a un valore ben preciso, che dagli studiosi di statistica viene assunto come probabilità dell’evento E.

La probabilità cosi determinata si chiama probabilità statistica 0 a posteriori, in quanto, attraverso la frequenza relativa, essa risulta nota soltanto dopo l’effettiva esecuzione delle prove sperimentali.

Come emerge dall’esempio appena considerato, il concetto base della teoria frequentista della probabilità è quello di frequenza relativa.

Per definizione:

Si chiama frequenza relativa dell’evento casuale E il rapporto tra il numero k delle volte in cui l'evento si è verificato e il numero n delle prove effettuate.

$$f(E)=k/n$$

Bisogna osservare che frequenza relativa di un evento casuale tende a divenire costante, al crescere del numero n delle prove effettuate nelle stesse condizioni. Ed è proprio tale valore, intorno al quale tende a stabilizzarsi f(E) al crescere di n, che si assume come probabilità dell’evento E.

Da questa definizione si comprende il motivo per cui si dice che nella definizione frequentista la probabilità è ricavata a posteriori dall’esame dei dati rilevati, mentre nella definizione classica la probabilità è stabilita a priori.

In base a queste considerazioni si può formulare la seguente legge sperimentale, detta legge empirica del caso:

«In una serie di prove ripetute nelle stesse condizioni, la frequenza relativa di un evento tende a stabilizzarsi intorno ad un valore ben preciso, al crescere del numero delle prove effettuate».

Sull’opportunità di assumere il valore a cui tende f(E) come stima approssimata di p(E) furono eseguiti molti esperimenti da diversi matematici del XIX secolo.

In base ai risultati sperimentali ottenuti, si è potuto ribadire la fiducia nella legge empirica del caso, detta anche legge dei grandi numeri, la quale può essere cosi riformulata:

«In un gran numero di prove, tutte eseguite nelle stesse condizioni, la frequenza relativa di un evento, di probabilità costante, ordinariamente si discosta di poco dalla probabilità di quell’evento, e l'approssimazione é, in generale, tanto maggiore quanto più grande è il numero delle prove ripetute.»

L’accettazione della legge dei grandi numeri conduce ad enunciare la definizione di probabilità di un evento secondo l’impostazione frequentista:

Si assume come probabilità dell’evento E il valore intorno al quale tende a stabilizzarsi la frequenza relativa dello stesso evento, all’aumentare del numero delle prove ripetute nelle stesse condizioni. Ossia:

$$p(E)≃f(E)=k/n$$

commettendo un errore che, in generale, diventa sempre più piccolo al crescere di n.

La probabilità di E, cosi definita, come abbiamo già detto, si chiama probabilità statistica o a posteriori.

La teoria frequentista è molto utilizzata nelle scienze sperimentali, nei casi ove non è possibile applicare la definizione classica. Con essa non si ottiene il valore esatto, ma soltanto una stima della probabilità di un evento casuale; questa stima è, in generale, tanto più attendibile quanto più elevato è il numero delle prove ripetute nelle stesse condizioni.

Occorre però dire che anche il campo di applicazione della probabilità statistica è limitato, in quanto non è possibile determinare la probabilità statistica di tutti gli eventi incerti.

Infatti, per poter dire che f(E) rappresenta una stima attendibile di p(E) occorre essere in grado di eseguire prove sperimentali ripetibili di quell’evento. Ossia, è necessario poter osservare il valore intorno al quale si stabilizza la frequenza al crescere del numero delle prove, tutte effettuate nelle stesse condizioni.

Esempio:
Vogliamo sapere quale sia la probabilità che si verifichi il seguente evento:
E = «Il giocatore Rossi fara centro nel prossimo tiro libero durante la partita di pallacanestro che si sta disputando.»

Evidentemente la probabilità teorica, $p(E) = 1/2 = 0.5$, non appare attendibile, in quanto esistono ragioni sufficienti per pensare che i casi possibili:
e₁ = «Rossi farà centro»
e₂ = «Rossi non farà centro»

non siano ugualmente probabili. Supponiamo di sapere che Rossi, in partite precedentemente disputate, su 100 tiri liberi abbia centrato il canestro 82 volte, e quindi la frequenza relativa di tale evento è:

$$f(E)=82/100=0,82$$

In base a questa informazione ci chiediamo se sia ragionevole assumere la frequenza $f = 0,82$ come stima attendibile della probabilità che Rossi faccia centro nella partita in corso, e quindi se sia esatto scrivere $p(E)≃f = 0,82$.

La risposta è, in generale, negativa in quanto, presumibilmente, le condizioni in cui Rossi si troverà ad eseguire il lancio nel corso di questa partita possono essere anche notevolmente diverse dalle condizioni in cui egli effettuati i 100 lanci nelle precedenti partite.

Potrebbero, infatti, essere cambiate le condizioni atmosferiche, l’arbitro, i giocatori della sua squadra e di quella avversaria, lo stato psicologico o fisico dello stesso Rossi, a causa di eventuali problemi finanziari, familiari, ecc.
Dunque, viene meno il concetto di "prove ripetute nelle stesse condizioni", caratteristico della definizione frequentista della probabilità.

Subentrano, a questo punto, considerazioni di carattere soggettivo sulle condizioni in cui il Rossi si troverà ad effettuare il tiro libero.

Coloro i quali ritengono che tali condizioni siano mutate di poco rispetto alle precedenti partite, o comunque che le variazioni non influiscano sull’esito del lancio, assumeranno $p(E)≃ f=0,82$, come stima attendibile dell’evento E = «Rossi farà centro».

Altre persone, invece, in base ad informazioni in loro possesso, possono giudicare che le condizioni siano mutate in modo rilevante, e quindi attribuire un diverso valore alla probabilità che si verifichi l’evento considerato.

Ad esempio, potrebbero avere saputo che il Rossi è dolorante al braccio destro, e ritenere che, per questo motivo, egli abbia minore probabilità di realizzare il canestro.

Dunque, anche nella teoria frequentista emerge il carattere soggettivo del concetto di probabilità.

Teoria soggettivista della probabilità

          

Come si è visto, esistono eventi in corrispondenza dei quali non è possibile determinare sia la probabilità teorica classica, sia quella secondo l’impostazione frequentista.

Ad esempio, appartengono a questa categoria eventi del tipo:

E₁ = «Mauro, nell’esame di maturità, sarà interrogato in fisica»
E₂ = «Nei prossimi mesi i prezzi degli immobili ad uso abitativo saliranno»
E₃ = «Domenica prossima il risultato della partita Juventus-Milan sarà 3-0»

Si tratta di situazioni il cui esito dipende da molte circostanze, ossia di eventi, per cosi dire, unici nel loro genere.

Di essi non si può calcolare né la probabilità teorica, in quanto i casi possibili o sono sconosciuti o non sono ugualmente probabili, né la probabilità a posteriori, ossia secondo l'impostazione frequentista, in quanto essa richiede di poter effettuare una sequenza di prove ripetute nelle stesse condizioni.

Tuttavia, nella pratica, è possibile dare una valutazione della probabilità anche di eventi di questo genere.

Ciò è testimoniato dal fatto che, a seconda di questa stima, Mauro seguirà con minore o maggiore attenzione le lezioni di fisica, uno speculatore acquisterà o venderà appartamenti, due tifosi scommetteranno una cena sull’esito della partita Juventus-Milan; tutti mossi dalla speranza di ricevere un beneficio in relazione all’evento considerato.

Esiste, dunque, ed è più comune di quanto si pensi, la possibilità di dare una valutazione soggettiva della probabilità di tutti quegli eventi dei quali non si può determinare né la probabilità teorica né quella statistica.

Questa stima soggettiva della probabilità è certamente meno affidabile di quelle ottenibili (quando è possibile) con i metodi precedenti, ma non per questo meno importante.

Esempio:
Dire che la probabilità di un evento E, secondo la stima di una certa persona, è

$$p(E)=0,25=25/100$$

significa dire che quella persona giudica equo pagare un prezzo di 25 euro per avere il diritto di ricevere 100 euro solo se l’evento E si verificherà (o, viceversa, farsi pagare 25 euro per sborsarne 100 solo se l’evento E non si verificherà).

Esempio:
Dire che Mauro valuta dell’80% la probabilità di essere interrogato in fisica nell’esame di maturità, significa affermare che Mauro giudica equo pagare un prezzo di 80 euro per avere il diritto di ricevere 100 euro solo se si verificherà il sudetto evento.

Se l’evento accadrà, allora Mauro avrà guadagnato 20 euro, altrimenti avrà perso le 80 euro pagati inizialmente.

Gianna, una compagna di Mauro, in base a sue opinioni personali, può invece ritenere che 'amico abbia soltanto la probabilità del 70% di essere interrogato in fisica, e quindi giudica equo pagare 70 euro per riceverne 100, solo se l’evento si realizzerà.

Si comprende che, secondo l'impostazione soggettivista, persone diverse possono formulare valutazioni differenti sulla probabilità dello stesso evento.

La diversità delle stime dipende dalla diversità delle conoscenze, delle opinioni, delle esperienze personali, e persino dal carattere di quelle persone. Tuttavia, la difformità delle opinioni individuali dovrà divenire concordanza di valutazioni, quando, dell’evento in esame, sia possibile determinare la probabilità teorica o quella statistica.

La teoria soggettivista si sviluppo negli anni venti per opera del filosofo inglese Ramsey, ma solo con De Finetti, massima autorità italiana in materia di calcolo delle probabilità, la concezione soggettivista della probabilità divenne una vera e propria teoria matematica.

Si deve, infatti, al De Finetti la seguente definizione rigorosa di probabilità soggettiva:

«La probabilità di un evento E, secondo l’opinione di un certo soggetto, é uguale al seguente rapporto:
$$p(E) =s/S$$
dove s è il prezzo che quel soggetto stima equo pagare per avere il diritto di ricevere il compenso S, solo se l'evento E si verificherà.»

Anche questa definizione, come si può facilmente intuire, non è esente da critiche in quanto si può confondere il soggettivismo con l’arbitrarietà.

Teoria assiomatica della probabilità

                 

Nel corso del tempo, furono proposte anche altre definizioni e si giunse al punto che numerosi matematici, partendo da definizioni diverse, si ripromettevano di ricostruire tutta la teoria della probabilità.

Verso il 1930 la situazione fu risolta da alcuni matematici russi che proposero di assiomatizzare la teoria della probabilità.

La teoria assiomatica permette di superare tutte le difficoltà precedentemente viste: simmetria dei risultati, numerosità degli esperimenti, soggettivismo nell’assegnazione dei valori di probabilità.

Infatti per costruire questa teoria non si parte più dal concetto di probabilità, ma da un certo numero di assiomi o proposizioni fondamentali non dimostrabili.

La definizione assiomatica di probabilità di un evento segue da tali assiomi ed è semplicemente: la probabilità di un evento è un numero che soddisfa agli assiomi del calcolo delle probabilità.

In questo modo la teoria della probabilità viene affrontata in modo più generale e accetta, come casi particolari, tutte le definizioni precedenti.

Formalmente, questa costruzione della teoria della probabilità è simile alla costruzione della geometri euclidea. La geometria euclidea parte infatti da alcuni assiomi, non dimostrabili, che definiscono implicitamente gli enti fondamentali della geometria stessa, come esempio punti e rette.

Definiti gli enti fondamentali, si può costruire tutta la geometria come conseguenza logica delle posizioni fatte, e quindi, si possono enunciare tutta una serie di teoremi dimostrabili, che permettono di costruire la geometria piana e la geometria solida euclidea.

Assiomi del calcolo della probabilità

   

Gli assiomi del calcolo delle probabilità soddisfano i requisiti che qualunque teoria assiomatica deve soddisfare, cioè, gli assiomi devono essere:

• semplici;
• il minor numero possibile;
• compatibili tra loro: due teoremi da essi dedotti non possono contraddirsi;
• completi: da essi si devono dedurre tutti i teoremi della teoria stessa;
• indipendenti: nessuno di essi deve essere una conseguenza logica degli altri.

Gli assiomi del calcolo delle probabilità, che soddisfano i requisiti precedenti furono enunciati da Kolmogorov in modo che la teoria delle probabilità fosse sviluppata in parallelo alla teoria degli insiemi.

Tenendo conto della rappresentazione grafica delle varie operazioni sugli insiemi/eventi.

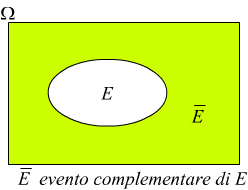
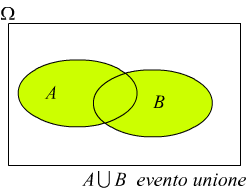
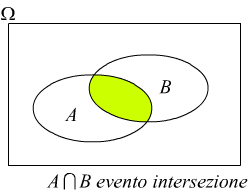
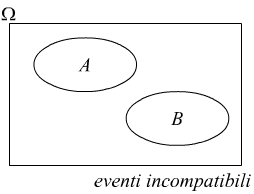
La teoria delle probabilità può essere costruita con i seguenti tre assiomi.

Assioma 1
La probabilità d un evento E in nello spazio campionario Ω è un numero reale non negativo.
$p(E)≥0$

Assioma 2
La probabilità dell’insieme spazio campionario Ω è 1.
$P(Ω)=1$

Assioma 3
Se gli eventi elementari e₁, e₂, .., e_n sono eventi a due a due incompatibili allora:
$p(E_1⋃E_2⋃... ⋃E_n)=p(E_1)+p(E_2)+...+p(E_n)$

Dagli assiomi precedenti si possono trarre alcune importanti conclusioni:

1° Per ogni evento E si ha
$0≤p(E)≤1$
cioè la probabilità del verificarsi di un qualsiasi evento E è sempre compresa tra 0 ed 1 estremi inclusi.

2° Se A e B sono due eventi ed A è contenuto in B allora
$p(A)≤p(B)$
$p(A⋂B)=p(A)$
$p(A⋃B)=p(B)$

3° Se $E↖{-}$ è il complemento di $E$ in $Ω$ si ha:
$p(E↖{-})=1-p(E)$

Poi, come si può notare dal 3° assioma se Ω è formato da tutti gli eventi elementari e₁, e₂,.., e_n si avrà

$p(Ω)=p(e_1)+p(e_2)+..+p(e_n)=1$

se ammettiamo l’equiprobabilità degli eventi, ovvero se ammettiamo che
$$p(e_1)=p(e_2)=..=p(e_n)=1/n$$

allora per qualsiasi evento composto E formato da m eventi elementari avremo:

$$p(E)=m/n$$

ritrovando in tal modo la formula della teoria di probabilità classica di Laplace.

Altre ricerche correlate

• Probabilità classica.
• Probabilità esercizi.
• Eventi e spazio campionario.
• Somma logica di eventi.
• Probabilità condizionata.