Calcolo delle probabilità

La probabilità è la misura dell'incertezza associata a un evento casuale; il calcolo delle probabilità nasce, dunque, dalla necessita di prevedere l’incerto.

Molte delle realtà che si presentano usualmente sono caratterizzate dall’incertezza su ciò che accadrà nel futuro. Il calcolo delle probabilità è il settore della matematica che si occupa di elaborare dei modelli per descrivere queste situazioni.

Nata originariamente dallo studio del gioco di azzardo questa tecnica matematica viene applicata oggi in molteplici altre discipline. Dall’Ottocento in poi il calcolo delle probabilità diventa uno strumento fondamentale nella fisica, nella biologia, nell’economia e nelle scienze sociali.

Oggi, le teorie dell’«incerto» pervadono ormai la vita quotidiana dell’uomo moderno, sempre più impegnato a cercar di prevedere l’esito dei più svariati eventi che lo riguardano direttamente: non solo giochi d’azzardo, dunque, ma soprattutto eventi naturali (terremoti, alluvioni, ecc.), scelte di tipo economico-finanziario, eventi relativi alle nascite e ai decessi, teoria delle assicurazioni (contro le malattie, gli infortuni sul lavoro, gli incidenti stradali, il furto e l’incendio, ecc.) e tanti altri eventi.

Esistono diversi metodi per definire, e quindi determinare, la probabilità di un evento casuale; nelle applicazioni si utilizza la definizione più opportuna, secondo il tipo di evento aleatorio considerato.

Gli approcci principali sono la teoria classica e la teoria frequentistica di probabilità.

Nella concezione classica la probabilità è stabilita a priori, prima di osservare i risultati di un esperimento.
Nella teoria frequentista la probabilità è ricavata a posteriori, esaminando i risultati dopo un numero congruo di prove.

La teoria classica è applicabile in tutti i casi in cui sia possibile attribuire una simmetria tra i possibili risultati elementari, vale a dire quando è possibile definire esattamente il numero di casi possibili tutti equiprobabili e, di conseguenza, il numero di casi favorevoli.

La varietà dei quesiti affrontati dal punto di vista probabilistico porta però ad applicare il concetto di probabilità anche a casi in cui manca o è difficile definire la simmetria tra i possibili risultati, come ad esempio calcolare l’aspettativa di vita di una persona a 10 anni, o la probabilità per un automobilista di avere un incidente il prossimo anno.

Il tal caso appare insufficiente applicare la teoria classica e si fa ricorso ad altre definizioni di probabilità quale ad esempio quella frequentista dove però per stabilire la probabilità di un evento è necessario eseguire un numero sufficientemente alto di prove, idealmente tendente ad infinito.

Definizione classica della probabilità

Consideriamo i seguenti eventi casuali:
E₁ = «Estraendo un numero nel gioco della tombola esce il 10»
E₂ = «Lanciando un dado esce il 5»
E₃ = «Nel lancio di una moneta esce croce»

Si intuisce che i tre eventi hanno un diverso grado di possibilità di verificarsi. Più precisamente, la nostra fiducia, dal punto di vista della realizzazione, è crescente dall’evento E₁ all’evento E₃ ci sembra, infatti, che l’evento E₃ si possa realizzare più facilmente degli altri due, nel corso di una determinata prova.

Ciò premesso, assegnato un evento aleatorio «E», occorre trovare un modo che permetta di misurare il grado di possibilità o, come si suol dire, la probabilità che quell’evento ha di realizzarsi.
Questa grandezza viene espressa da un numero, che si indica con: p(E) e che si chiama probabilità dell’evento E.

Secondo la teoria classica abbiamo la seguente definizione di probabilità:

La probabilità p(E) di un evento «E» è il rapporto fra il numero m dei casi favorevoli (al verificarsi di «E» ) ed il numero n di tutti i casi possibili.

$$p(E)=m/n$$

Esempio:
Calcoliamo la probabilità che, nel lancio di un dado non truccato si realizzi il seguente evento:

E = «Esce un numero pari»

Osserviamo che, nel lancio di un dado, i casi possibili, ossia i fatti che possono accadere, sono rappresentati dai numeri
1, 2,3,4,5,6, ciascuno dei quali figura su di una faccia del dado.

Indicato con n il numero di tali casi, evidentemente si ha n=6.

L’evento E si verifica se, nel lancio del dado, esce uno dei numeri 2, 4, 6.

Ciascuno di essi rappresenta un caso favorevole al verificarsi di E, ossia una distinta modalità con cui l'evento E puo realizzarsi; indicato con m il numero di questi casi favorevoli, si ha m=3.

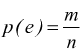
calcolo delle probabilità

Sapendo, inoltre, che il dado non è truccato, non ci sono ragioni per pensare che un numero esca più facilmente di un altro, cosicché si attribuisce la stessa fiducia al realizzarsi di ciascuno dei predetti casi possibili.

Ciò premesso, si assume come misura della probabilità dell’evento E il seguente numero:

$${p(E)}↙{⏟}↙\text"probabilità"=m↖{⏞}↖\text"casi favorevoli"/n↙{⏟} ↙\text"casi possibili"=3/6=1/2=0,5$$

ossia: il rapporto tra il numero dei casi favorevoli all’evento E e il numero di tutti i casi possibili, essendo questi ultimi ugualmente possibili.

Dunque, è 0,5, oppure, se si preferisce, è del 50% la probabilità che nel lancio di un dado si realizzi l’evento consistente nell’uscita di un numero pari.

Esempio:
Calcoliamo la probabilità che, estraendo una carta da un mazzo nuovo di 40 carte, si verifichi l’evento:

E = «Esce un asso»

Nell’estrazione di una carta dal mazzo considerato, sono 40 i casi possibili: uno per ogni carta del mazzo. Poiché il mazzo è nuovo, e quindi non vi sono carte «segnate», non si ha ragione di pensare che una carta possa essere estratta più facilmente di un’altra: i casi possibili, cioè, sono ugualmente possibili. Per quanto riguarda i casi favorevoli ai verificarsi di E, essi sono rappresentati dai 4 eventi elementari seguenti:

e₁ = «Esce l’asso di spade»
e₂= «Esce l’asso di bastoni»
e₃= «Esce I'asso di denari»
e₄= «Esce I'asso di coppe»

Dunque, essendo:
n = 40 il numero dei casi possibili
m = 4 il numero dei casi favorevoli
la probabilità di E risulta:

$$p(E)=4/40=1/10=0,1$$

Esempio:
Calcoliamo la probabilità che ciascuno dei seguenti eventi:
E₁ = «Esce un numero maggiore di 90»
E₂ = «Esce uno dei numeri 13, 17, 51»
E₃ = «Esce un numero compreso tra 1 e 90»
ha di realizzarsi durante una estrazione nel gioco della tombola.

In questo problema i casi possibili sono rappresentati dai numeri 1, 2, 3, .., 89, 90, quindi il loro numero è n = 90. Questi casi, inoltre, sono ugualmente possibili (equiprobabili) in quanto non vi sono ragioni valide per ritenere che uno di essi sia estratto piu facilmente di un altro.

Per quanto riguarda i casi favorevoli al realizzarsi dei vari eventi si ha:

1 nessuno dei casi possibili è favorevole all’evento E₁. Si puo anche dire che I'insieme dei casi favorevoli al realizzarsi di E₁, l’insieme vuoto; di conseguenza E₁ è un evento impossibile. Essendo:

Essendo:
n =90 il numero dei casi possibili
m= 0 il numero dei casi favorevoli
la probabilità di E₁, risulta nulla, infatti si ha:

$$p(E_1)=0/90=0$$

2 I casi favorevoli al realizzarsi dell’evento E₂ sono rappresentati ciascuno dai tre eventi elementari seguenti:
e₂₁ = «Esce il 13»
e₂₂ = «Esce il 17»
e₂₃ = «Esce il 51»

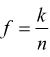
probabilità classica

Dunque, essendo:
n =90 il numero dei casi possibili
m= 3 il numero dei casi favorevoli
la probabilità che E₂ ha di verificarsi è:

$$p(E_2)=m/n=3/90=1/30$$

3 Consideriamo, ora, l’evento E₃. Si comprende facilmente che tutti i casi possibili sono anche favorevoli al verificarsi di E₃; in altre parole, vale la seguente uguaglianza:
(insieme dei casi favorevoli) = (insieme dei casi possibili)
Dunque, E₃ è un evento certo ed essendo n = m = 90, la sua probabilità risulta uguale ad uno; infatti:

$$p(E_3)=90/90=1$$

In tutti questi casi viene applicata la formula $p=m/n$.
Poiché l'insieme dei casi favorevoli è un sottoinsieme di quello dei casi possibili si ha sempre

$0≤m≤m$

Dividendo tutti i termini per n, si ha:

$$0≤m/n≤1$$

e quindi risulta:

$$0≤p(E)≤1$$

La probabilità di un qualsiasi evento «E» è un numero sempre compreso tra 0 e 1.

In particolare, indicati con

Ω l’evento certo
∅ l’evento impossibile

si ha:

$$p(Ω)=m/n=n/n=1$$ $$p(∅)=m/n=0/n=0$$

Riassumendo, per la probabilità di un evento si hanno i seguenti casi:

$$evento\{\table certo, p(Ω)=1 ; incerto, 0<p(E)<1 ; impossibile , p(∅)=0 $$

Evento complementare

Nel lancio di un dado, consideriamo l’evento casuale:
$E$ = «Esce uno dei numeri 1, 2»
Ad esso, utilizzando la negazione logica not, si può far corrispondere il nuovo evento seguente:

$E↖{-}$ = «Non esce uno dei numeri 1, 2» =
= «Esce uno dei numeri 3, 4, 5, 6»

chiamato evento complementare di $E$, che si verifica se e solo se non si verifica $E$.

L'evento complementare di $E$ è anche chiamato evento contrario dello stesso evento $E$.

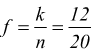
probabilità dell'evento contrario

Per quanto concerne le probabilità di questi eventi, si calcola facilmente che:

$$p(E)=2/6$$ $$p(E↖{-})=4/6$$

Si vede, poi, che vale la seguente relazione:

$$p(E)+p(E↖{-})=2/4+4/6=1$$

Si dice evento complementare dell’evento $E$ quel particolare evento $E↖{-}$ che si verifica se e solo se non si verifica $E$. Tra le probabilità di $E$ e di $E↖{-}$ vale la seguente relazione:

$$p(E)+p(E↖{-})= 1$$

Infatti, si ha:
n = numero dei casi possibili
n = numero dei casi favorevoli ad E
n- m = numero dei casi favorevoli ad E
e quindi:

$$p(E)+p(E↖{-})= m/n+{n-m}/n={m+n-m}/n=1$$

Calcolo combinatorio e calcolo delle probabilità

In diversi casi, il calcolo combinatorio consente di determinare più facilmente il numero dei casi possibili e quello dei casi favorevoli, relativi a eventi casuali di una certa complessità.
Una volta che n ed m siano noti, è poi immediato calcolare la probabilità dell’evento considerato.

Esempio:
Vogliamo determinare la probabilità che, nel lancio contemporaneo di due monete, si verifichi l’evento casuale:
E = «Le due monete si presentano con facce diverse»

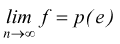
Nel lancio di due monete i casi possibili sono rappresentati dai seguenti eventi elementari:

e₁ = «Esce (testa, testa)»
e₂ = «Esce (testa, croce)»
e₃ = «Esce (croce, testa)»
e₄ = «Esce (croce, croce)»

quindi il loro numero è n = 4.

Il numero dei casi favorevoli è, ovviamente, m =2, perciò l’evento considerato ha la seguente probabilità di realizzarsi:

$$p(E)=2/4=1/2=0,5$$

Il numero dei casi possibili si poteva anche determinare mediante il calcolo combinatorio. Infatti, si osserva che:

$n=D'_{2,2}=2^2= 4$

ossia, i casi possibili sono tanti quante le disposizioni con ripetizione degli oggetti testa, croce presi a due a due.

Esempio:

Vogliamo determinare la probabilità che, nel lancio simultaneo di 3 monete, si verifichi il seguente evento:

E = «Le tre monete si presentano con la stessa faccia»

I casi possibili, nel lancio contemporaneo di tre monete, sono tanti quante le disposizioni con ripetizione di due oggetti (testa e croce), presi a tre a tre; ossia si ha:
(CCC),(CCT),(CTC),(CTT),(TCC),(TCT),(TTC),(TTT)

$n=D'_{2,3}=2^3=8$

I casi favorevoli al verificarsi di E sono rappresentati dagli eventi elementari:
e₁ = «Esce (testa, testa, testa)»
e₂ = «Esce (croce, croce, croce)»
e quindi si ha m=2.

La probabilità di risulta quindi la seguente:

$$p(E)=m/n=2/8=1/4=0,25$$

Esempio:
Nella prova consistente nel lancio di due dadi, vogliamo determinare la probabilità dell’evento casuale:

E = «Escono due numeri aventi somma uguale a 8»

Nel lancio di due dadi, i casi possibili sono tanti quanti le disposizioni con ripetizione di n = 6 oggetti, presi a due a due, ossia si ha:

$n=D'_{6,2}=6^2=36$

I casi favorevoli al verificarsi di E sono rappresentati dalle seguenti coppie:

(2,6) (3,5) (4,4) (5,3) (6.2)

il cui numero è m = 5.
Di conseguenza, la probabilità di E risulta essere:

$$p(E)=m/n=5/36=0,14$$

Esempio:
Ci proponiamo di determinare la probabilità che, nel gioco del Lotto, su di una certa ruota, si verifichi l'evento casuale:

E = «Viene estratto un terno prefissato»

Come è noto, i numeri del gioco del Lotto sono i naturali da 1 a 90; su ogni ruota ne vengono estratti cinque.

Si tratta di calcolare la probabilità che tra i 5 numeri estratti figurino i tre numeri prefissati. Poiché in tale gioco l’ordine non ha importanza, il numero dei casi possibili è dato dal numero delle combinazioni semplici di n = 90 numeri, presi a k=5 a k= 5, così possiamo scrivere:

$$n=C_{90,5}= (\table 90;5 )$$

Il numero dei casi favorevoli ad E è pari al numero delle combinazioni semplici di n =87 numeri, presi a k=2 a k=2; infatti, supponendo che dai 90 numeri si tolgano i tre prefissati e che, dei rimanenti 87, si costruiscano tutte le combinazioni semplici a 2 a 2, si può aggiungere a ciascuna di esse la terna prefissata, precedentemente tolta, ottenendo così tutte le possibili cinquine contenenti il dato terno. Possiamo quindi scrivere:

$$m=C_{87,2}= (\table 87;2 )$$

$$p(E)=m/n=(\table 87;2 )/ (\table 90;5 )=1/{11748}$$

Esempio:
Data un’urna contenente 40 palline delle quali 28 sono bianche e 12 sono rosse, ci proponiamo di determinare la probabilità che si verifichino i seguenti eventi, relativi all’estrazione contemporanea di due palline dall’urna:
E₁ = «Le palline sono entrambe bianche»
E₂ = «Le palline sono entrambe rosse»
E₃ = «Le palline sono di diverso colore»
Quale di essi risulta il più probabile?

Poiché le due palline vengono estratte contemporaneamente, allora l’ordine non è distinguibile, sicché i casi possibili sono tanti quante le combinazioni semplici di 40 oggetti, presi a 2 a 2; quindi si ha:

$$n=C_{40,2}= (\table 40;2 )=780$$

casi favorevoli al verificarsi di E₁ sono tanti quante le combinazioni semplici di 28 oggetti, presi a 2 a 2; sicché possiamo scrivere:

$$m_1=C_{28,2}= (\table 28;2 )=378$$

e quindi risulta:

$$p(E_1)=m_1/n=378/780=0,48$$

I casi favorevoli al verificarsi di E₂ sono tanti quante le combinazioni semplici di 12 oggetti presi a 2 a 2, ossia:

$$m_2=C_{12,2}= (\table 12;2 )=66$$

e quindi risulta:

$$p(E_2)=m_2/n=66/780=0,08$$

casi favorevoli al verificarsi di E₃ sono tanti quante le coppie di palline di diverso colore; poiché 28 sono le bianche e 12 le rosse, allora il numero delle predette coppie sarà:

$m_3=28⋅12=446$

La probabilità dell’evento E₃ risulta, quindi, la seguente:

$$p(E_3)=m_3/n=336/780=0,43$$

Si conclude che tra gli eventi considerati, quello che ha maggior probabilità di verificarsi è l’evento E₁.

Limiti della teoria di probabilità classica

Come si è visto La probabilità di un evento casuale E, calcolata secondo la definizione classica di Laplace, detta probabilità teorica o a priori, si calcola matematicamente come rapporto tra il numero m dei casi favorevoli al verificarsi dell'evento E e il numero finito n dei casi possibili; di conseguenza, per poter applicare la formula:

$$p(E)=m/n$$

indispensabile conoscere a priori m ed n, e inoltre occorre sapere che i casi possibili sono equiprobabili, ossia che hanno tutti la stessa probabilità di realizzarsi.

Nei giochi d’azzardo (dadi, tombola, Lotto, carte, ...) queste condizioni sono, in generale, soddisfatte, ossia è relativamente semplice conoscere il numero dei casi favorevoli e quello dei casi possibili, e inoltre, se le regole del gioco sono rispettate, i casi possibili sono da ritenersi equiprobabili.

Dunque, in generale. nei giochi d’azzardo si può calcolare la probabilità a priori di un evento aleatorio senza grandi difficoltà, applicando, quindi, la formula $p(E) = m/n$.

Esistono, pero, molti altri eventi casuali per i quali non si riesce a calcolare la probabilità teorica, a causa della difficoltà, o più spesso impossibilita, di conoscere il numero dei casi favorevoli e quello dei casi possibili; inoltre, qualora questi ultimi siano noti, non sempre si è in grado di stabilire con certezza se essi siano equiprobabili.

Appare impossibile calcolare la probabilità a priori di eventi quali i seguenti:

E₁ = «Domani piovera»
E₂ = «Mario, oggi trentenne, raggiungerà l’età di ottanta anni»
E₃ = «Nella corsa automobilistica di domenica prossima vincerà la Ferrari»
E₄ = «Nei prossimi mesi il prezzo dell’oro scenderà» ..etc..

Dunque, è evidente che, volendo usare il calcolo delle probabilità nello studio della realtà nel suo complesso, cioè nella previsione di eventi di tipo meteorologico, sociale, economico, ecc., l’uso della teoria classica, e quindi della probabilità teorica 0 a priori, si rivela molto limitato.

E’ allora necessario introdurre altri metodi e teorie che consentano di determinare la probabilità di più vaste classi di eventi aleatori.

Un’altra critica che viene mossa alla definizione di probabilità secondo l’impostazione di Laplace, riguarda la sua presunta oggettività.

La probabilità teorica di un evento casuale sembra, infatti, avere carattere di oggettività (essendo basata unicamente su considerazioni matematiche relative al numero dei casi favorevoli e a quello dei casi possibili), mentre, in realtà, presenta aspetti di soggettività: ossia, la probabilità di un evento casuale può risultare diversa a seconda di chi vuole calcolarla. Infatti, per potere applicare la formula $p = m/n$ si richiede che:

«i casi possibili siano ugualmente possibili»

e cioé che abbiano la stessa probabilità di realizzarsi.
Sorge, quindi, il problema di sapere giudicare se due eventi siano o no equiprobabili; ma, per risolverlo, occorrerebbe applicare la stessa formula $p = n/m$, cadendo cosi in un inevitabile giro vizioso.

Questa incongruenza certamente non sfuggi a Laplace che, nel tentativo di superarla, ricorse al cosi detto principio di ragion sufficiente, in base al quale si stabilisce che:

Due eventi casuali sono da considerarsi equiprobabili quando non vi siano ragioni sufficienti per pensare che uno di essi possa verificarsi più facilmente dell’altro.

Si sono state e ci sono obiezioni sulla validità generale di questo principio.
Tuttavia, noi qui ci limitiamo a far osservare che esso presenta la possibilità di esprimere valutazioni di carattere soggettivo sulla equiprobabilità degli eventi casuali.

Di conseguenza, l’oggettività del concetto di probabilità teorica di un evento è, in realtà, soltanto apparente. Questi limiti della teoria di probabilità classica di Laplace hanno sicuramente contribuito alla nascita della cosidetta teoria frequentistica delle probabilità.

Altre ricerche correlate