Probabilità condizionata e prodotto logico di eventi
Si definisce probabilità di un evento A condizionata (subordinata) all'evento
B e si indica P(A|B), la probabilità che si verifichi A nell'ipotesi che
B sia verificato. Si hanno eventi dipendenti se
le informazioni fornite dall'evento B vanno poi ad alterare le probabilità
del verificarsi del successivo evento A.
Viene definita dalla relazione:
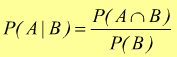
Ovviamente si deduce:
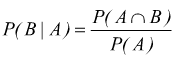
In queste scritture
● P(A) è la probabilità che
si verifichi l'evento A.
● P(B) è la probabilità che si verifichi l'evento
B.
● P(A|B) è la probabilità
che si verifichi l'evento A dopo che si è verificato l'evento B.
● P(B|A) è la probabilità
che si verifichi l'evento B dopo che si è verificato l'evento A.
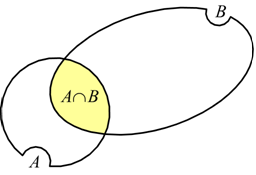
● P(A ∩ B) è la probabilità
che in un singolo tentativo si verifichino simultaneamente l'evento A e
l'evento B.
Nel caso di eventi dipendenti tra loro, il teorema del prodotto può, dunque, essere sinteticamente espresso delle uguaglianze
![]()
La probabilità dell'intersezione tra due eventi è uguale al prodotto delle probabilità di uno degli eventi per la probabilità condizionata dell'altro, purchè sia verificato il primo evento.
Eventi indipendenti
Due eventi A e B si dicono indipendenti se
il verificarsi dell'uno non influenza il verificarsi dell'altro.
Nel lancio di due dadi il risultato di uno non influenza il risultato
dell'altro; però se si estraggono due carte
da un mazzo ( senza reimmissione ) la probabilità di avere una carta
rossa la seconda volta è legata al fatto di avere incontrato o no una
carta rossa la prima volta: questi eventi sono dipendenti.
Se gli eventi A e B sono indipendenti fra loro risulta:
![]()
in tal caso:
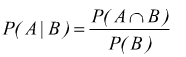
 cioè
cioè ![]()
similmente si ha:
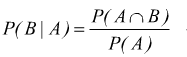
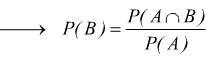 cioè
cioè ![]()
La probabilità che in un singolo tentativo si verifichino tutti gli eventi indipendenti di un insieme è pari al prodotto delle singole probabilità.
Estendendo il teorema all'intersezione di più eventi:
![]()
infatti ponendo F=A∩B
![]()
![]()
![]()
Il teorema del prodotto viene ulteriormente semplificato nel caso gli eventi siano collettivamente indipendenti quando ogni evento risulta indipendente non solo dagli altri, ma anche da tutte le possibili intersezioni; quando risulta
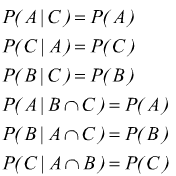
allora, il teorema del prodotto per tre eventi indipendenti diventa
![]()
generalizzando per n eventi indipendenti E1 , E2 , ... , En :
![]()
Esempio eventi dipendenti : si lanciano 2 dadi,
sapendo che la somma dei punti ottenuta è minore di 7, calcolare la probabilità
che i due dadi abbiano lo stesso valore .
Gli eventi sono
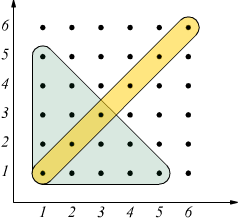
A = somma dei punti minore di 7 : 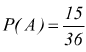
B = dadi con lo stesso valore : 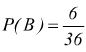
la probabilità che i due eventi si verifichino in un unico tentativo è 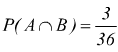
seguendo la definizione, la probabilità che i due dadi abbiano lo stesso valore sapendo che la somma dei loro punti è un numero minore di 7 è
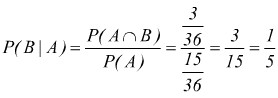
in questo caso gli eventi sono dipendenti e questo lo si riconosce dal fatto che risulta P(B|A) ≠ P(B).
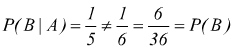
Esempio eventi indipendenti : Calcolare la probabilità che estraendo una carta da un mazzo da 40 si tratti di una carta nera supponendo che sia uscita una figura.
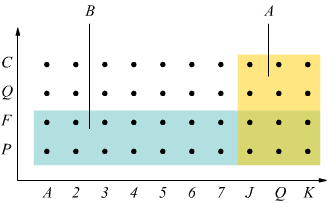
A = si estrae una figura
B = si estrae una carta nera
notiamo che se è stata già estratta una figura(A) la probabilità che si tratti di una carta nera (B) è
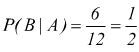
mentre se è stata estratta una carta nera (B), la probabilità che si tratti di una figura (A) è

è evidente l'intersezione dei due insiemi 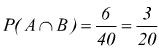
chiaramente è 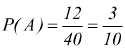 mentre
è
mentre
è 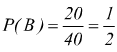
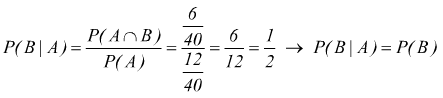
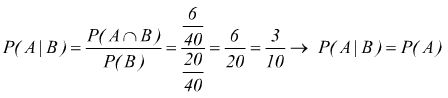
 edutecnica
edutecnica