Eventi
Gli eventi sono quei fenomeni che avvengono nel mondo ordinario e che possono essere osservati o misurati attraverso i sensi o strumenti di misurazione.
Gli eventi si verificano in un determinato momento e luogo, e possono essere di natura diversa: essi possono essere spontanei oppure organizzati, cioè provocati.
Il calcolo delle probabilità è nato per studiare i giochi d’azzardo in epoca rinascimentale per studiare gli eventi casuali, vale a dire eventi che, come i giochi d’azzardo, hanno un esito imprevedibile a priori e quindi hanno un risultato casuale.
Nei periodi precedenti del medioevo il concetto di evento casuale, veniva respinto, in quanto si credeva al disegno provvidenziale di Dio che guidava tutti gli eventi.
Nel XVII secolo, la passione per il gioco d’azzardo spinse alcuni giocatori incalliti a porre dei quesiti ad alcuni dei più celebri matematici dell’epoca.
Per rispondere a questi problemi è necessario studiare gli eventi casuali e determinare le probabilità del verificarsi di ciascun evento.
Dallo studio degli eventi casuali nacque allora la teoria delle probabilità, soprattutto ad opera di B. Pascal, P. Fermat e G. Bernoulli.
In breve tempo ci si rese conto che questa teoria poteva avere applicazioni molto più vaste di quelle dei giochi d’azzardo per cui era inizialmente nata, e nel corso del tempo si svilupparono interi settori di applicazione : A. A. Cournot applicò lo studio del calcolo delle probabilità ai fenomeni economici, mentre altre notevoli applicazioni si ebbero in settori quali le scienze attuariali (assicurazioni), scienze naturali (leggi sull’ereditarietà dei caratteri genetici) e scienze fisiche (meccanica quantistica), ma per parlare di teoria delle probabilità bisogna dal principio parlare di eventi.
Classificazione degli eventi
Gli eventi possono essere classificati in tre categorie principali:
- eventi certi;
- eventi impossibili;
- eventi incerti;
consideriamo i seguenti avvenimenti o eventi:
- $E_1$ = «Nel gioco della tombola, durante una estrazione, esce un numero compreso tra 1 e 90»
- $E_2$ =«Lanciando un dado esce un numero compreso tra 1 e 6»
- $E_3$ = «Acquistando tutti i biglietti di una lotteria si vince il primo premio»
Si capisce facilmente che tali eventi si verificheranno con certezza, è quindi vengono chiamati eventi certi.
Consideriamo, ora, questi altri eventi:
- $E_4$ = «Lanciando un dado esce il numero 13»
- $E_5$ = «Il sole tramonta a est»
- $E_6$ = «Estraendo 5 carte da un normale mazzo da poker,escono tutti assi»
Si vede che questi eventi, al contrario dei precedenti, non si verificheranno mai, e quindi sono chiamati eventi impossibili.
Accanto a questi eventi ne esistono moltissimi altri che possono verificarsi, ma la cui realizzazione non è sicura, e perciò sono chiamati eventi incerti.
Ad esempio, sono incerti i seguenti eventi:
- $E_7$ = «Estraendo una carta da un mazzo da briscola esce un re»
- $E_8$ = «Nel lancio di un dado esce il 4»
- $E_9$ = «Nel lancio di una moneta esce testa»
La loro realizzazione dipende essenzialmente dal caso e, per questo motivo, essi sono chiamati eventi casuali o aleatori.
Spazio campionario
Si dice spazio campionario e si indica col simbolo Ω, l’insieme di tutti i possibili esiti di un evento casuale (aleatorio).
Dato uno spazio campionario Ω, si chiama evento (o partizione) ogni sottoinsieme di Ω.
Uno spazio campionario può essere finito o infinito.
Esempio 1:
lanciamo un dado non truccato e osserviamo quale numero esce.:
Spazio campionario:
i possibili esiti dell’esperimento sono sei dunque è
Ω={1,2,3,4,5,6}:
Esempio di evento:
E=esce un numero pari
dunque il sottoinsieme corrispondente è
E={2,4,6}:
Esempio 2 :
lanciamo una moneta successivamente due volte e consideriamo se esce testa T o croce C.
Spazio campionario:
L’esperimento ha quattro possibili esiti per ciascuno dei due lanci successivi:
Ω={(T,T);(T,C);(C,T);(C,C)}
Esempio di evento:
E=esce testa almeno una volta
dunque il sottoinsieme corrispondente è
E={(T,T);(T,C);(C,T);}
Esempio 3 :
Lanciamo successivamente una moneta per valutare il numero del lancio in cui esce croce per la prima volta.
Spazio campionario:
Il risultato di questo spazio campionario può essere qualsiasi numero naturale diverso da zero, dunque:
E=N-{0}
Esempio di evento:
E=esce croce la prima volta dopo il terzo tentativo
dunque il sottoinsieme corrispondente è:
E={(x∈Ω | x>3}
Come si vede, ogni evento aleatorio ha il suo spazio campionario che può essere finito o infinito, come si può notare nell’ultimo caso.Inoltre, dobbiamo notare la nomenclatura usata in queste circostanze.
Si ha un evento elementare quando il sottoinsieme degli eventi è un unico evento appartenente allo spazio campionario.
Si ha un evento composto quando il sottoinsieme degli eventi è costituito da un numero finito di elementi dello spazio campionario.
Si ha un evento certo quando il sottoinsieme degli eventi coincide con l’intero spazio campionario.
Si ha un evento impossibile quando il sottoinsieme degli eventi coincide con l’insieme vuoto.
Ad esempio se nel lancio di un dado esce 3, si ha un evento elementare; se esce un numero compreso tra 2 e 5 si ha un evento composto, se esce un numero minore di 7 si ha un evento certo; se esce un numero maggiore o uguale a 7 si ha un evento impossibile.
Eventi ed insiemi
Avendo definito gli eventi come sottoinsiemi dello spazio campionario risulta utile osservare i parallelismi esistenti tra teoria degli insiemi ed eventi di uno spazio campionario.
Assegnati due eventi A e B appartenenti allo spazio campionario Ω avremo seguenti casi:
Unione di A e B e si indica A⋃B l’evento che si verifica quando si verificano A o B o entrambi.
Intersezione di A e B e si indica A⋂B l’evento che si verifica quando si realizzano entrambi gli eventi A e B.
Si definisce evento contrario di A e si indica con A, l’evento che si verifica quando non si realizza A, ossia l’evento rappresentato dal complementare di A: A=Ω-A.
Ipotizziamo ad esempio il lancio di un dado e i due eventi:
A: esce un numero maggiore 2
B: esce un numero minore di 5
Si ha lo spazio campionario Ω={1,2,3,4,5,6} dunque:
A⋃B=Ω
perché qualsiasi numero uscente soddisfa A o B.
A⋂B={3,4}
perché sono i numeri che soddisfano simultaneamente gli eventi A e B.
A={1,2}
evento contrario di A.
B={5,6}
evento contrario di B
Un’altra nozione importante è quella di eventi incompatibili.
Due eventi si dicono incompatibili quando la loro intersezione è vuota. Si dicono compatibili in caso contrario.
Questo accade quando il verificarsi di un evento esclude il verificarsi dell’altro.
Ad esempio, nel lancio di un dado
A: esce un numero dispari
B: esce il 4
sono due eventi incompatibili
La rappresentazione insiemistica di due eventi incompatibili è la seguente.
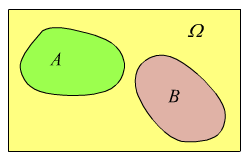
Se per lo stesso lancio avessimo ipotizzato
A: esce un multiplo di 3
B: esce un numero pari
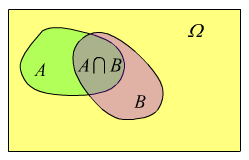
avremmo avuto due eventi compatibili dato che A⋂B={6};
qui di seguito la rappresentazione grafica di due eventi compatibili
I chiusura a questo discorso sugli eventi e sullo spazio degli eventi riportiamo uno schema di sintesi tra la nomenclatura usata nella teoria degli insiemi e quella prevista per il calcolo delle probabilità.
| Notazione | Teoria degli insiemi | Calcolo probabilità |
| Ω | Insieme universo | Spazio campionario |
| a∈Ω | a è un elemento di Ω | {a} è un evento elementare |
| A⊆Ω | A è un sottoinsieme di Ω | A è un evento |
| A=Ω | A è l’insieme universo | A è evento certo |
| A=∅ | A è l’insieme vuoto | A è evento impossibile |
| A | A è il complementare di A | A è l’evento contrario di A |
| X=A⋃B | X è l’unione di A e B | X è l’evento A o B |
| X=A⋂B | X è l’intersezione di A e B | X è l’evento A e B |
| A⋂B=∅ | A e B sono disgiunti | A e B sono eventi incompatibili |
 edutecnica
edutecnica