Collisioni e conservazione della quantità di moto

     

Nella dinamica del punto materiale, le definizioni di impulso di forza e di quantità di moto si riferiscono sempre ad un sistema isolato cioè ad un contesto dove sono presenti solo forze conservative e l'energia totale del sistema ( energia cinetica + energia potenziale) si conserva.

Dunque, in un sistema isolato la quantità di moto totale del sistema si conserva, cioè si mantiene costante e si è già visto che questa è una conseguenza dei principi della dinamica.

La variazione della quantità di moto di un singolo corpo rigido o di una particella dotata di massa può avvenire come conseguenza dell'impulso di forza che esso riceve:

      

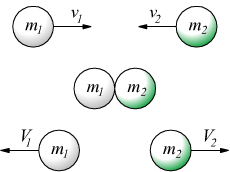L'applicazione del principio di conservazione della quantità di moto si presta in modo particolare quando avviene una collisione tra due corpi rigidi in assenza di forze esterne (sistema isolato).

Durante un urto due corpi che collidono, si comportano come un sistema isolato: la loro quantità di moto si conserva.

In questa uguaglianza le grandezze v₁ e v₂ sono le velocità delle masse prima dell'urto, mentre V₁ e V₂ sono le velocità delle stesse masse dopo l'urto. Tutte le velocità sono grandezze fisiche vettoriali ma se ipotizziamo, per il momento, che la collisione avvenga su una linea retta la notazione vettoriale può essere omessa.

Urto frontale elastico

          

Se, nella collisione, oltre alla conservazione della quantità di moto si ha una conservazione dell'energia totale si ha un urto elastico.

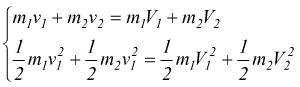
note le velocità delle due masse v₁ e v₂ prima dell'urto è possibile ottenere le velocità V₁ e V₂ successive all'urto. Infatti semplificando il termine costante ½.

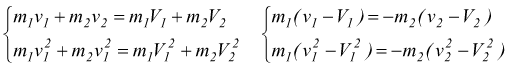
sostituendo

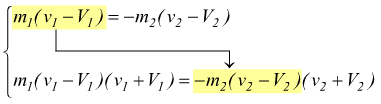
Ottenendo

Sostituendo questa nell'equazione della quantità di moto

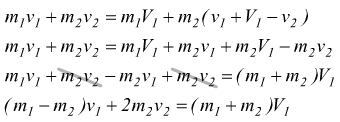
cioè: 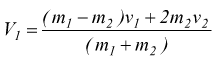                    In modo analogo si può procedere per esplicitare V₂.

In conclusione si ha:

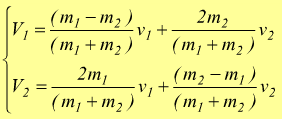
In questa pagina riportiamo un simulatore di urti elastici tra masse lungo una stessa direzione.

Urto frontale anelastico

          

Un urto potrebbe essere anelastico, in tal caso non si ha la conservazione dell'energia cinetica. Un caso particolare di questa eventualità è un urto completamente anelastico, quando i due corpi dopo la collisone rimangono solidali e procedono alla stessa velocità finale.
In un urto completamente anelastico si ha la sola conservazione della quantità di moto

          

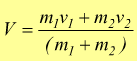
avendo indicato in questo caso con V la velocità dei due corpi che rimangono uniti dopo l'urto.

Urti obliqui

          

Non tutte le tipologie di collisione che possono avvenire fra corpi rigidi possono essere ricondotte agli urti collineari (sulla stessa linea retta) anzi in generale le traiettorie finali degli oggetti risultano oblique tra loro.
Questo avviene appunto perchè la quantità di moto

     è una quantità vettoriale; quindi l'operazione algebrica

deve essere eseguita vettorialmente. Il caso più semplice possibile da studiare è costituito da due corpi sferici di identica massa m. Se ipotizziamo un urto elastico con una massa inizialmente in movimento e l'altra ferma notiamo che, se i due baricentri non sono perfettamente allineati, le traiettorie di uscita delle due sfere sono determinate dalle equazioni

          

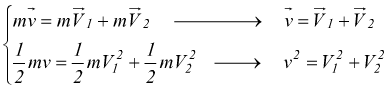
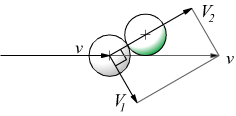
queste due condizioni concomitanti impongono che le velocità ( e traiettorie) finali delle due masse siano perpendicolari tra loro.

Pendolo balistico

          

Il pendolo balistico è un dispositivo meccanico in grado di misurare la velocità di un proiettile. Un proiettile dotato di velocità iniziale v e di massa m, viene fatto entrare in collisione con una massa M appesa e vincolata tramite un cavo in estensibile.

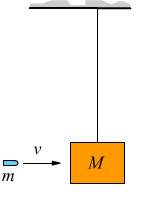
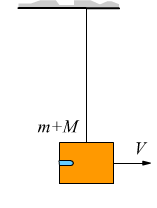
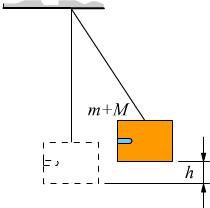
L'urto è anelastico perché il proiettile rimane conficcato completamente nella massa M bersaglio. La massa risultante m+M si mette in moto con velocità iniziale V e dunque per la conservazione della quantità di moto:

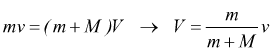
la massa risultante inizia il suo moto con energia cinetica 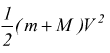; questa massa si sposta rimanendo appesa al vincolo fino a raggiungere un altezza h dove l'intero sistema m+M ha energia potenziale (m+M)gh.
Per il principio di conservazione dell'energia E_c=U_p :

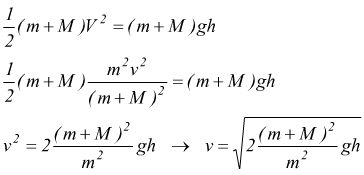
la velocità del proiettile si deduce con la formula

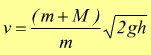
Urti con la molla

          

Nei problemi sulla dinamica degli urti, è presente talvolta la molla, il cui comportamento è regolato dalla legge di Hooke ; con una energia potenziale 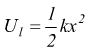; con k=costante di elasticità [N/m] ed x=allungamento [m].

Un esempio tipico è dato dalla collisione su un piano orizzontale privo di attrito tra due masse m ed M con quest'ultima inizialmente ferma e vincolata da una molla a riposo; mentre la massa m si muove verso di essa a velocità v.

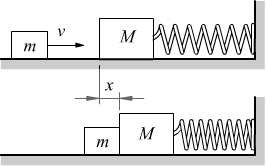
Si viene a verificare un urto anelastico dopo il quale le due masse si muovono solidali con la stessa velocità V comprimendo la molla.
Essendo l'urto anelastico:

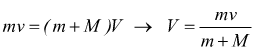
dopo l'urto, per l'intero sistema si avrà un'energia cinetica complessiva:

che sarà assorbita dall'energia potenziale della molla E_c=U_l:

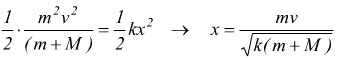
in questo modo si ottiene l'accorciamento x della molla. Dato che la molla passa dalla posizione di riposo alla posizione di massima compressione il tempo dell'accorciamento deve essere ¼ del periodo .

           

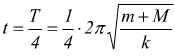
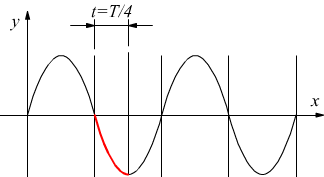
Nel caso vi sia la presenza dell'attrito bisogna considerare nel bilancio delle energie anche quest'ultimo. Infatti dopo la collisione il sistema di masse sarà interessato da una resistenza di attrito pari a

con f_d = coefficiente di attrito del piano; quindi anche il bilancio delle energie deve essere corretto

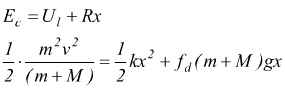
come si vede la resistenza di attrito si aggiunge all'energia potenziale elastica della molla per contrastare l'energia cinetica della massa.