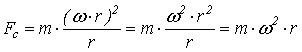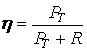La dinamica è quella parte della meccanica che studia la relazione tra le forze e movimenti. E' costruita su tre principi fondamentali.

I° principio (principio di inerzia)
Un corpo tende a mantenere il suo stato di quiete o di moto rettilineo uniforme, se non interviene una forza esterna a cambiare tale stato.

II° principio (principio di proporzionalità)
Se ad un corpo si applica una forza continua costante, esso si muove di moto uniformemente accelerato, in direzione della forza. Il rapporto tra la forza applicata e l'accelerazione ottenuta è costante ed è pari alla massa del corpo.

III° principio (principio di azione e reazione)
Ad ogni azione corrisponde sempre una reazione uguale contraria.

Principio di D'Alembert
Per i principi della dinamica le forze agenti su un corpo vengono classificate in: Forze esterne che applicate al corpo che ne fanno variare il moto (F). Forze esterne e forze d'inerzia che contrastano le variazioni del moto
(m· a)

La forza esterna F si oppone al prodotto - m·a che viene chiamato forza d'inerzia. Questo può essere ritenuto valido per un corpo che si muove nello spazio in condizioni ideali ed in assenza di attriti. Nella realtà fra le forze esterne si devono considerare, che oltre alle forze attive, anche le forze resistenti (reazioni vincolari, attriti, etc..). Quindi alla forza attiva F si deve sottrarre anche l'eventuale risultante delle forze passive che possiamo chiamare R. Il principio di Alembert afferma che : Durante il moto (accelerato) di un corpo si fanno equilibrio in ogni momento, le forze esterne, attive e resistenti e le forze di inerzia agenti sul corpo.

1) se il moto è uniforme su un piano orizzontale, essendo la velocità costante a=0 e quindi ma=0

La forza motrice è uguale alla forza resistente

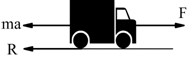
2) se il moto è accelerato la forza motrice deve equilibrare la forza di inerzia e la forza resistente:

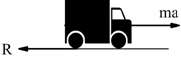
3) se il moto è decelerato (manca la forza motrice) l'accelerazione è negativa per cui il vettore ma ha verso contrario rispetto al caso precedente: la forza di inerzia favorisce il moto mentre la forza resistente lo contrasta.

4) se il moto è uniforme verso l'alto su un piano inclinato; la forza d'inerzia (ma) è nulla ma si deve considerare la componente P_T della forza peso che si oppone alla salita.

5) se il moto è accelerato verso l'alto su un piano inclinato; la forza d'inerzia non è nulla.

6) se il moto è in discesa su un piano inclinato; con moto accelerato, sotto l'effetto della componente P_T della forza-peso si ha:

Impulso di forza e quantità di moto

Consideriando ancora l'equazione fondamentale della dinamica



Moltiplichiamo entrambi i membri per il tempo


Ma il fattore a ·t=v nel moto uniformemente accelerato è la velocità finale raggiunta da un corpo dotato dell'accelerazione a dopo un tempo t. Avremo dunque :



Il prodotto F·t è detto impulso di forza. La quantità di moto è una grandezza vettoriale ed ha la stessa direzione della velocità . Il prodotto mv è detto quantità di moto.

La prima legge si può esprimere anche come: una particella libera si muove sempre con quantità di moto costante.

Principio di conservazione della quantità di moto: La quantità di moto totale di un sistema composto da due particelle soggette soltanto alla loro mutua interazione rimane costante.

Come indicato in figura

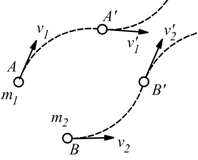
all'istante t la particella 1 si trova in A con velocità V₁ e la particella 2 si trova in B con velocità V₂. In un istante successivo t' le particelle si trovano in A' e B' con velocitàV₁' e V₂'. Se indichiamo con m₁ ed m₂ le rispettive masse delle due particelle:

Nell'istante successivo t' avremo:

Per il principio di conservazione della quantità di moto avremo:

Un'interazione fra due particelle produce uno scambio di quantità di moto, cosicché la quantità di moto persa da una delle due particelle è uguale alla quantità di moto guadagnata dall'altra particella.

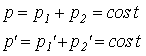
Sottraendo membro a membro

Cioè
                  quindi:
                                                       differenziando rispetto al tempo t:


La forza è la derivata rispetto al tempo della quantità di moto. (secondo principio della dinamica).
L'equazione precedente diventa:

Quando due particelle interagiscono , la forza agente su una particella è uguale ed opposta alla forza agente sull'altra (che poi coincide col terzo principio della dinamica).

Sapendo che la massa m è costante

              cioè:

Forze di attrito

Ogni volta che due corpi sono in contatto, come nel caso di un oggetto posto su un tavolo, si manifesta una resistenza che si oppone al moto relativo dei due corpi. Supponiamo per esempio di spingere un oggetto lungo il tavolo, imprimendogli una certa velocità. Dopo che la spinta è cessata, l'oggetto rallenta e alla fine si ferma.

Questa perdita di quantità di moto è indicativa di una forza che si oppone al moto; la forza è chiamata attrito radente. Si può sperimentare e dimostrare che la forza associata all'attrito radente che si oppone al moto dell'oggetto vale:

N è la forza normale che preme un corpo contro l'altro, f è una costante di proporzionalità detta :
coefficiente di attrito.

Le considerazioni valgono anche se il piano di attrito è inclinato

Si riconosce che:

                      dividendo membro a membro:       

Si può anche notare che :          la forza di attrito vale in questo caso:

  se F>R il grave comincia a scivolare in discesa;

il grave resta fermo finché       

tornando ai casi precedenti del moto di un corpo su un piano inclinato, viene definito rendimento di un piano inclinato il rapporto:

con

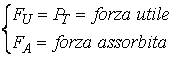Quindi il rendimento del piano è

Attrito volvente

Questo è un tipo di attrito che si ha quando un corpo cilindrico ruota su un piano

Considerata la semilunghezza b di una lunghezza simmetrica 2b rappresentativa la lunghezza della superficie di contatto, l'equazione di equilibrio alla rotazione è:

      il coefficiente      è il coefficiente di attrito volvente
In condizioni di moto uniforme F=R, per cui:

L'attrito volvente è proporzionale alla pressione normale e dipende dalla natura delle superfici a contatto. Valori tipici dell'attrito volvente sono:
f_v=0,015÷0,035 autoveicoli su strada
f_v=0,002÷0,003 veicoli su rotaia

Moto curvilineo

Se la forza ha la stessa direzione della velocità, il moto è rettilineo . Per produrre moto curvilineo la forza risultante deve formare un angolo diverso da zero con la velocità, in modo che l'accelerazione abbia una componente perpendicolare alla velocità che renda conto del cambiamento di direzione del moto.
Se la massa è costante, la forza deve essere parallela all'accelerazione (2°principio) infatti forza e accelerazione sono grandezze vettoriali e nella   esse devono essere cospiranti.

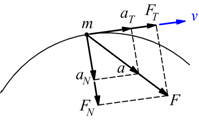Secondo lo schema illustrato deve essere:

Dove ρ è il raggio di curvatura dato che  

La forza tangenziale è responsabile della variazione in modulo (in intensità) della velocità mentre la forza centripeta è responsabile della variazione in direzione della velocità. Se la forza tangenziale è nulla non si ha accelerazione tangenziale e il moto è circolare uniforme. Se la forza normale (centripeta) è nulla si ha moto rettilineo. Nel caso particolare di moto circolare ρ=R

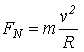     essendo           avremo:     

Per il moto uniforme, l'unica accelerazione è a_N che si può anche scrivere nella forma
(prodotto scalare) pertanto :

Forza centrifuga

Caratterizza un corpo che percorre una traiettoria curva, agisce continuamente su di esso con una spinta rivolta verso l'esterno della curva. Questa spinta tende ad allontanare il corpo dal centro di rotazione e viene chiamata appunto forza centrifuga.
Dal secondo principio della dinamica abbiamo: F=m·a Nel caso della forza centrifuga avremo l'accelerazione centrifuga:   F_c=m·a_c .

Ricordandoci che l'accelerazione centripeta è 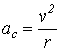          dove r è il raggio della curvatura

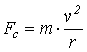
F_c=forza centrifuga ( e centripeta ) [N]
m=massa del corpo [kg]
v= velocità periferica [m/sec]
r= raggio di rotazione [m]

Volendo esprimere la forza F_c in funzione della velocità angolare