Vettore induzione magnetica e campo magnetico
Il vettore induzione magnetica B [T] o [Wb/m2] può essere definito formalmente dalla relazione
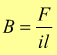
già vista nella pagina sull'interazione tra il campo magnetico e la corrente elettrica. In questa formula, F è la forza che subisce il filo lungo l, attraversato dalla corrente i; disposto perpendicolarmente alle linee del campo.
Viene introdotto il vettore campo magnetico H [Asp/m] legato al vettore induzione magnetica B dalla relazione
![]()
Dove μ=μr·μo è il coefficiente
di permeabilità magnetica;
μo =permeabilità magnetica del vuoto=4π·10-7
m·kg/C2
μr=permeabilità magnetica relativa: dipendente dal materiale
L'intensità del campo magnetizzante nell'aria (o nel vuoto) Ho
misurato in amperspire/m [Asp/m], ha una espressione molto semplice
che può essere ottenuta dagli esempi già visti.
1] Intensità di un campo magnetico Ho in un punto distante R da un conduttore percorso dalla corrente I.

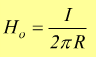
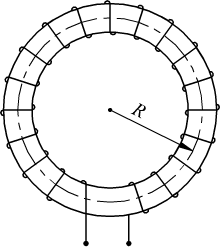
2] Intensità di un campo magnetico Ho all'interno di un solenoide toroidale di raggio medio R, costituito da N spire percorse dalla corrente I.
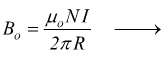
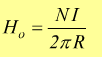
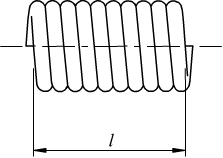
3] Intensità del campo magnetico Ho all'interno di un solenoide di forma allungata, di lunghezza l e costituito da N spire, percorso dalla corrente I.
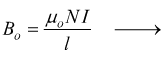
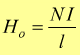
|
Induzione Magnetica |
Campo magnetico H in Asp/cm
e permeabilità magnetica mr |
|||||||||
|
Ferro e acciaio dolce |
Lamiere normali |
Lamiere di silicio |
Ghisa |
Aria |
||||||
|
B |
H |
µr |
H |
µr |
H |
µr |
H |
µr |
H |
|
|
0,10 |
0,7 |
1.140 |
0,45 |
1.775 |
0,8 |
1.000 |
2,0 |
400 |
800 |
|
|
0,20 |
0,9 |
1.780 |
0,5 |
3.200 |
1,0 |
1.600 |
4,5 |
355 |
1.600 |
|
|
0,30 |
1,0 |
2.400 |
0,6 |
4.000 |
1,25 |
1.920 |
8,0 |
300 |
2.400 |
|
|
0,40 |
1,2 |
2.660 |
0,7 |
4.570 |
1,45 |
2.200 |
13,0 |
246 |
3.200 |
|
|
0,50 |
1,4 |
2.860 |
0,9 |
4.450 |
1,6 |
2.500 |
20,0 |
200 |
4.000 |
|
|
0,60 |
1,7 |
2.820 |
1,3 |
3.690 |
1,8 |
2.630 |
28,0 |
171 |
4.800 |
|
|
0,70 |
2,2 |
2.500 |
1,7 |
3.290 |
2,0 |
2.800 |
40,0 |
140 |
5.600 |
|
|
0,80 |
2,7 |
2.370 |
2,3 |
2.780 |
2,5 |
2.560 |
55,0 |
117 |
6.400 |
|
|
0,90 |
3,2 |
2.250 |
3,3 |
2.180 |
3,1 |
2.320 |
80,0 |
90 |
7.200 |
|
|
1,00 |
4,0 |
2.000 |
4,7 |
1.700 |
4,0 |
2.000 |
110,0 |
73 |
8.000 |
|
|
1,10 |
5,0 |
1.750 |
6,3 |
1.395 |
5,0 |
1.760 |
150,0 |
58 |
8.800 |
|
|
1,20 |
6,2 |
1.550 |
8,0 |
1.200 |
7,0 |
1.370 |
200,0 |
48 |
9.600 |
|
|
1,30 |
8,5 |
1.230 |
10,5 |
990 |
12,0 |
867 |
|
|
10.400 |
|
|
1,40 |
12,0 |
930 |
13,5 |
830 |
23,0 |
487 |
|
|
11.200 |
|
|
1,50 |
20,0 |
600 |
18,0 |
567 |
40,0 |
300 |
|
|
12.000 |
|
|
1,60 |
35,0 |
365 |
31,0 |
413 |
75,0 |
171 |
|
|
12.800 |
|
|
1,70 |
60,0 |
226 |
32,0 |
262 |
140,0 |
97 |
|
|
13.600 |
|
|
1,80 |
100,0 |
144 |
90,0 |
160 |
240,0 |
60 |
|
|
14.400 |
|
|
1,90 |
160,0 |
95 |
148,0 |
103 |
|
|
|
|
15.200 |
|
|
2,00 |
250,0 |
64 |
300,0 |
53 |
|
|
|
|
16.000 |
|
Energia di magnetizzazione
Per formare un campo magnetico occorre una certa quantità di energia
che viene fornita dal circuito elettrico che lo ha generato.
Si può dunque esprimere l'energia per unità di volume accumulata nello
spazio in cui il campo magnetico è apprezzabile:
 [ J/m3 ]
[ J/m3 ]
essendo un energia specifica, per unità di volume, l'energia totale vale E=w·V.
Tensione magnetica
La tensione magnetica (in analogia alla tensione elettrica) calcolata lungo una linea chiusa che può essere anche coincidente con una linea di forza, è uguale alla sommatoria delle correnti concatenate con il percorso scelto. Cioè si può esprimere:
![]() [ Asp ]
[ Asp ]
Se in particolare la linea chiusa (di lunghezza l) è concatenata N volte con un circuito, ad esempio nel caso di un solenoide si ha:
![]() o
più precisamente
o
più precisamente  [
Asp ]
[
Asp ]
Al termine NI viene dato il nome di forza magneto-motrice. (f.m.m.)
essa si misura in amperspire.
Bisogna insistere sul termine 'linea chiusa' perché non ha senso parlare
di percorso aperto, dovendosi verificare il concatenamento con le correnti
, che a loro volta sono dovute a percorsi chiusi.
Circuiti magnetici
Un circuito magnetico è un percorso chiuso in cui vengono concentrate
le linee di induzione magnetica B. Sono circuiti magnetici i solenoidi
toroidali, le colonne e i gioghi dei trasformatori.
Qui sotto è disegnato un circuito magnetico con due traferri che sono
i punti più delicati, assorbendo una notevole quantità di amperspire;
perciò i traferri vanno eliminati o ridotti al minimo indispensabile.
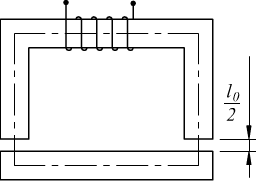
Legge di Hopkinson
Consideriamo un circuito magnetico formato da più tronchi con sezioni, lunghezze, e permeabilità relative diverse; si può dimostrare che sussiste la relazione fra la f.m.m. NI e il flusso magnetico φ nel circuito, è dato da:
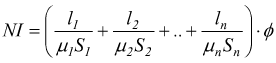
con l , μ ed S che sono rispettivamente, lunghezza, permeabilità e sezione del tronco. Al generico termine
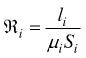 [
H-1 ] si da il nome di riluttanza
(del tronco)
[
H-1 ] si da il nome di riluttanza
(del tronco)
E' importante contenere la riluttanza complessiva del circuito magnetico
per richiedere a parità di flusso desiderato bassi valori di f.m.m.
NI. La riluttanza dei traferri costituisce in genere il termine di gran
lunga più grande di tutta l'intera riluttanza.
La legge di Hopkinson può anche essere riscritta, indicando con ℜT
la riluttanza totale.
![]()
Nel caso di circuiti magnetici con tronchi in parallelo e serie-parallello,
per il calcolo, valgono le stessi leggi analoghe ai principi di Kirchoff.
Si ha, ad un nodo magnetico:
![]()
cioè: la somma dei flussi entranti uguaglia la somma dei flussi uscenti.
Per ciascun percorso chiuso soggetto a più f.m.m. la loro somma algebrica
uguaglierà la somma delle cadute di tensione magnetiche dei vari tronchi
che formano il circuito chiuso in esame:
![]()
Nel caso di un elettromagnete, la forza (meccanica ) portante è espressa per i due poli dalla relazione
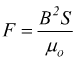 [
N ]
[
N ]
Autoinduttanza
Quando una corrente scorre in una bobina (o in un solenoide), viene prodotto nella bobina un flusso di campo magnetico variabile. Questo, a sua volta, induce una forza elettromotrice sulla bobina stessa. La forza elettromotrice indotta si oppone alla variazione di flusso che l'ha generata (legge di Lenz). Per esempio, se l'intensità di corrente che scorre nella bobina aumenta, il conseguente flusso in crescita induce una forza elettromotrice che si oppone alla corrente originaria tendendo a ritardare la sua crescita. Se l'intensità di corrente nella bobina, invece, diminuisce, il flusso è decrescente e induce una forza elettromotrice che produce una corrente con lo stesso verso di quella originaria, in modo da opporsi alla diminuzione.

Il flusso magnetico φ che passa attraverso N spire della bobina è proporzionale alla corrente (i) nella bobina; possiamo, così, viene definita l'autoinduttanza L (o induttanza):

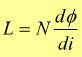 [
Henry] [H]=[Ω×s]
[
Henry] [H]=[Ω×s]
Di conseguenza la forza elettromotrice indotta in una bobina con autoinduttanza L, dotata di N spire diviene, per via della legge di Faraday :
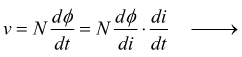
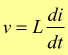
L'intensità di L dipende dalla geometria e dalla presenza o meno di
un materiale ferromagnetico all'interno della bobina.
L'autoinduttanza può essere definita per ogni circuito o per ogni parte
di un circuito.
I circuiti, infatti, mostrano sempre una certa induttanza, che però,
in genere, è molto piccola, a meno che non siano presenti nel circuito
bobine con molte spire. Una bobina che possieda un' autoinduttanza L
significativa viene chiamato induttore; nei diagrammi dei circuiti,
l'induttore viene rappresentato mediante il simbolo.
![]()
L'eventuale resistenza che un induttore possiede, dovrebbe sempre essere
rappresentata a parte (separatamente).
Gli induttori possono avere molte utili applicazioni, in genere, in
un circuito elettronico, è meglio evitare che ci sia induttanza.
Un discorso diverso riguarda invece gli impianti elettrici domestici
ed industriali.
In essi la presenza di induttori è palese e necessaria, infatti, se
c'è un induttore c'è un campo magnetico e l'interazione tra campi elettrici
e campi magnetici è indispensabile per produrre azioni meccaniche tramite
i motori elettrici (lavatrici, macchine utensili etc..).
Nel caso di un solenoide di N spire l'autoinduttanza può essere
espressa anche come
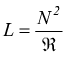
Mutua induttanza
Se due bobine sono disposte una di fianco all'altra, come disegnato sotto, una corrente variabile nella bobina 1 induce una forza elettromotrice nella bobina 2.
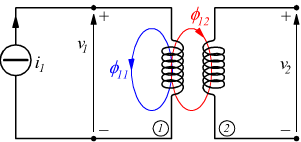
Si nota come il flusso concatenato nella bobina 1 è
![]()
per il discorso fatto sull'autoinduttanza
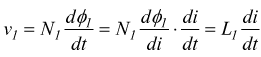 mentre
mentre
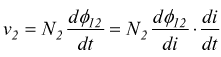 se
definiamo
se
definiamo
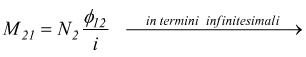
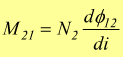
per cui è 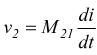
M21 viene chiamata mutua induttanza
e mette in relazione la corrente sulla bobina 1 con la tensione ai capi
della bobina 2.
M21 è una costante nel senso che non dipende dalla corrente
i; essa dipende da fattori geometrici come le dimensioni , la forma,
il numero di spire e la posizione relativa delle due bobine e anche
dal fatto che esista un eventuale traferro.
Si può anche considerare la situazione inversa:
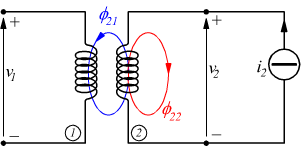
il flusso concatenato nella bobina 2 è ![]()
 mentre
mentre
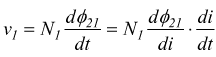 si
definisce
si
definisce
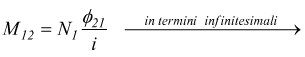
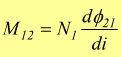
per cui è 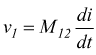
Si può dimostrare che M12=M21=M e che vale la relazione
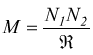
Un trasformatore
è un esempio di mutua induttanza nel quale l'accoppiamento viene ottimizzato
in modo che, praticamente, tutte le linee di flusso del campo magnetico
passino attraverso entrambe le bobine.
I trasformatori sono apparecchiature che permettono di aumentare o diminuire
una corrente alternata.
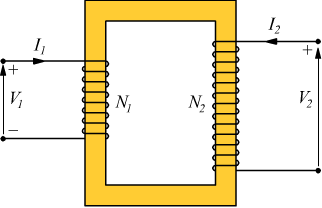
Un trasformatore è costituito da due avvolgimenti (o bobine) detti
primario e secondario. Le due bobine possono essere intrecciate mediante
un filo isolante oppure collegate attraverso un nucleo di ferro come
disegnato sopra.
I trasformatori vengono fabbricati in modo tale che pressoché tutto
il flusso magnetico originato dal circuito primario costituito da N1
spire passi attraverso il circuito secondario costituito da N2
spire. Se il flusso concatenato φ è lo stesso, per la legger di
Faraday si avrebbe:
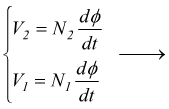
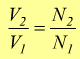
Un trasformatore ben progettato può avere un rendimento anche del 99% tuttavia la potenza elettrica trasferita al secondario non potrà mai essere maggiore di quella che si ha al circuito primario. Sapendo che la potenza elettrica è P=VI
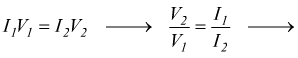
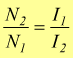
Idealmente, nel caso di accoppiamento perfetto, (assenza di flussi dispersi) se L1 ed L2 sono le induttanze dei due avvolgimenti si ha
![]() in
pratica, però
in
pratica, però ![]()
con k che rappresenta il coefficiente di accoppiamento che può variare da 1 (massimo accoppiamento possibile) a zero (disaccoppiamento).
Ferromagnetismo
Un campo magnetico può essere prodotto da materiali magnetici o da correnti elettriche. Materiali magnetici comuni sono i magneti ordinari , i nuclei di ferro dei motori e degli elettromagneti , i supporti magnetici delle memorie dei calcolatori e le strisce magnetiche delle carte di credito.
Un qualunque oggetto di ferro può essere trasformato in un magnete
di forte intensità.
Questi materiali vengono chiamati ferromagnetici.
L'origine del ferromagnetismo può essere spiegata, infatti, le ricerche
a livello microscopico hanno rivelato che un campione di ferro è diviso
in regioni sottili dette domini magnetici ,o domini di Weiss le cui
dimensioni in lunghezza e larghezza sono inferiori al millimetro . Ogni
singolo dominio si comporta come un piccolo magnete con il suo polo
nord e il suo sud. Un campione di ferro non magnetizzato contiene molti
domini disposti in modo casuale,come illustrato nel disegno:
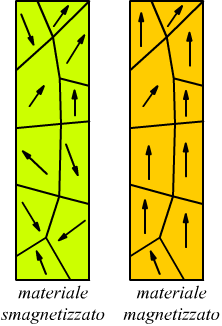
gli effetti magnetici dei singoli domini si annullano l'uno con l'altro
e di conseguenza il campione di ferro risulta non magnetizzato. in un
magnete, invece, i domini sono allineati prevalentemente lungo una direzione
come mostrato nel secondo disegno (in questo caso sono tutti orientati
verso l'alto).
E' possibile trasformare un campione di ferro non magnetizzato in un
magnete immergendolo in un campo magnetico intenso.
Un magnete di ferro è in grado di rimanere magnetizzato per lungo tempo
,e per questo viene detto magnete permanente,
se però si sbatte il magnete a terra o lo si prende a martellate si
possono rimescolare i domini in maniera casuale in modo che il magnete
perda in parte o del tutto le sue proprietà magnetiche.
Un magnete permanente può perdere il proprio magnetismo anche a causa
di un riscaldamento.
L'innalzamento della temperatura accresce il moto di agitazione termica
degli atomi aumentando la disposizione casuale dei domini.
Al di sopra di una certa temperatura (temperatura di Curie=1043°K per
il ferro) il ferromagnetismo scompare del tutto .
Isteresi magnetica
Il campo magnetico all'interno di un lungo solenoide è direttamente proporzionale alla corrente che vi scorre , infatti è
![]()
Questa formula è valida solo se all'interno del solenoide è presente
il vuoto o l'aria. Se inseriamo nel solenoide un materiale ferromagnetico,
il campo verrà enormemente accresciuto.Questo in conseguenza del fatto
che i domini presenti nel materiale ferromagnetico risulteranno allineati
a causa dell'esistenza del campo magnetico esterno. Il campo magnetico
risultante può essere espresso come
![]()
Bo è dovuto alla sola presenza della corrente nel solenoide
(campo esterno) mentre BM è il campo addizionale dovuto alla
presenza del materiale ferromagnetico; risulta BM >>Bo
.
In modo più sintetico si potrà scrivere
![]()
Introducendo la permeabilità magnetica μ=μo·μr prototto tra la permeabilità magnetica assoluta e la permeabilità magnetica relativa, caratteristica del materiale ferromagnetico.
Le misure sulle proprietà dei materiali ferromagnetici vengono eseguite
solitamente usando un solenoide toroidale.
Supponiamo che il nostro solenoide contenga inizialmente un nucleo di
ferro non magnetizzato e che nelle sue spire non scorra corrente. Se
aumentiamo lentamente la corrente I, Bo cresce lentamente
con I. Anche il campo totale B, aumenta seguendo però la linea curva
illustarata nella figura .
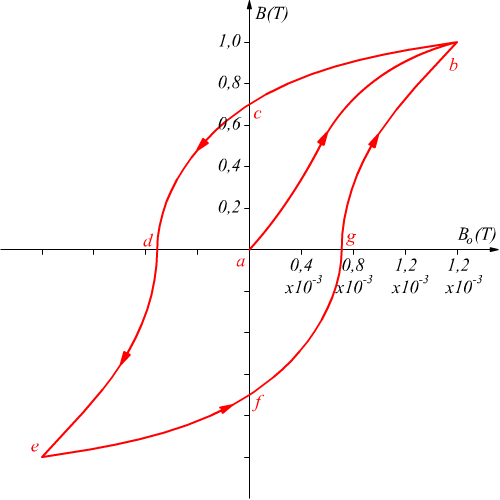
Nel punto (a) del grafico, i domini del materiale, sono orientati casualmente.
Al crescere di Bo i domini cominciano ad allinearsi sempre
di più fino a raggiungere la situazione relativa al punto (b) ferro
sta per raggiungere la saturazione. Nel punto (b) dove sono tutti allineati,
raggiungendo in questo modo la saturazione.
Si nota come la scala di grandezza di B sia molto maggiore di quella
di Bo (circa mille volte più grande).
Supponiamo poi di ridurre il campo esterno Bo facendo diminuire
la corrente che diventerà nulla nel punto (c).
L'orientamento dei domini non tornerà completamente casuale, un certo
magnetismo continua ad esistere.
Invertendo il senso della corrente possiamo portare il materiale alla
situazione iniziale di completo disordine (d) in modo che sia B=0.
Se questa corrente inversa continua a crescere il ferro tenderà a raggiungere
la saturazione in direzione opposta (e).
Infine riportando la corrente a zero e facendola di nuovo crescere nel
senso originale il campo totale seguirà il cammino (efgb) raggiungendo
di nuovo la saturazione nel punto (b).
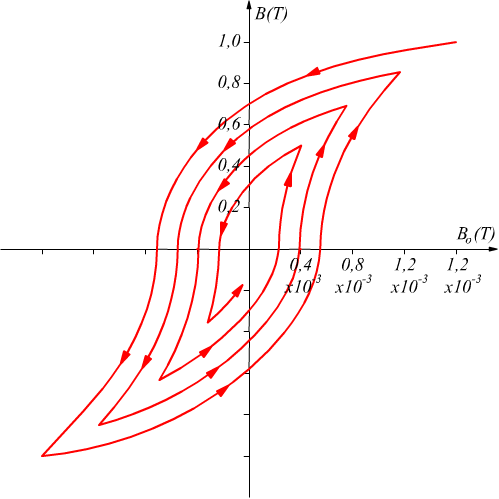
Il fenomeno sopra descritto viene chiamato isteresi magnetica. La curva (bcdefgb) è chiamata curva di isteresi. Un materiale ferromagnetico può essere completamente smagnetizzato attraverso una inversione ripetuta della corrente, accompagnata da una sua progressiva diminuzione
 edutecnica
edutecnica