Trasformatore elettrico

      

I trasformatori trovano largo impiego nella risoluzione del problema del trasporto di energia elettrica a grandi distanze. Tradizionalmente la corrente elettrica viene prodotta in forma alternata sinusoidale

poiché generata da speciali macchine rotanti: gli alternatori; questi sono dispositivi azionati da turbine meccaniche come ad esempio accade nelle centrali idroelettriche che sfruttano l'energia potenziale dei salti d'acqua. Queste centrali si trovano spesso in remote località montane, a notevole distanza dai centri urbani nei quali viene utilizzata l'energia elettrica. Nasce, dunque, il problema di trasferire tale energia dal luogo di produzione a quello di utilizzo.

E' possibile dimostrare che trasferire energia elettrica in regime alternato sinusoidale è più vantaggioso rispetto al regime stazionario (corrente continua). Il trasformatore è un dispositivo che consente di risolvere in modo brillante questo processo di trasferimento.

Il trasformatore è una macchina elettrica che funziona solo in corrente alternata e viene usato per trasformare potenza elettrica da un livello di tensione ad un altro. Non esiste un dispositivo equivalente per il regime stazionario.

La formula che esprime la potenza (energia sull'unità di tempo) su un carico puramente resistivo in corrente alternata è

dove ɸ è l'angolo tra i due vettori tensione V e corrente I. In questa formula V ed I sono i valori efficaci di tensione e corrente con

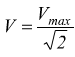   ed    

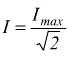
Nei due esempi che seguono assumeremo per semplificare

A Partendo da una centrale idroelettrica, supponiamo di dover trasferire una tensione generata
E=1000 kV con
I=500 A
lungo una linea elettrica che oppone una resistenza costante
R=250Ω
la potenza erogata è
la potenza persa è     

B Ora raddoppiamo la corrente e dimezziamo la tensione, quindi la potenza erogata P_e rimane invariata.
E=500 kV con
I=1000 A
R=250Ω
la potenza erogata è  
la potenza persa è      

Da questi valori si conclude come il criterio generale per il trasporto di energia elettrica sia quello di trasferire con la massima tensione e con la minima corrente.

A monte e a valle della linea di trasmissione troveremo dei trasformatori: a monte per innalzare il più possibile il livello di tensione e a valle per abbassare il livello di tensione e per permettere all'utenza di operare in adeguate condizioni di sicurezza .
Qui sotto è schematizzato un esempio di sistema di distribuzione di energia elettrica con dei valori tipici.

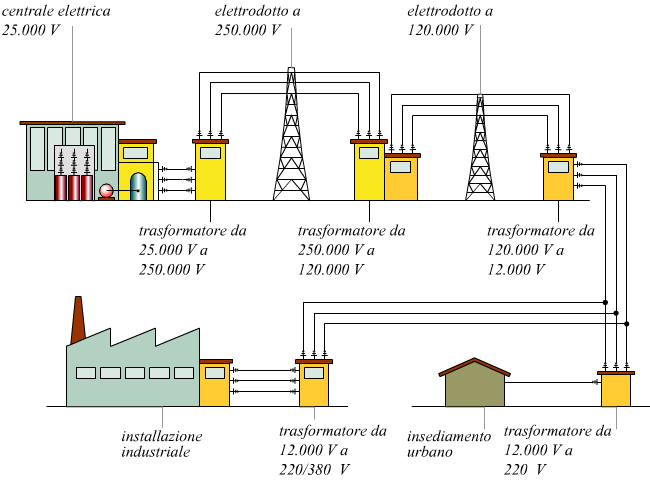
Trasformatore ideale

      

Il trasformatore è costituito da un nucleo magnetico e da almeno due avvolgimenti.
Gli avvolgimenti sono classificati in base al numero di spire, quello ad alta tensione (AT) con più alto numero di spire (a sezione minore) e quello di bassa tensione (BT) con un minor numero di spire (a sezione maggiore).

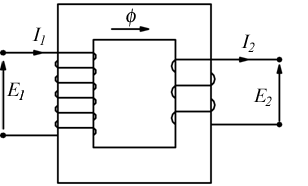
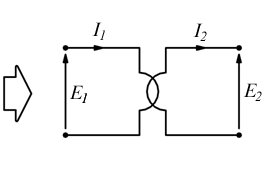
Trasformatore monofase ideale (caratteristiche)

      

1 Accoppiamento perfetto tra le bobine, il flusso creato da un avvolgimento si concatena perfettamente con l'altro.
2 Perdite trascurabili, sia nel rame che nel ferro.
3 Bassa riluttanza del circuito magnetico.
4 La potenza apparente in ingresso è uguale alla potenza apparente in uscita.

Riferendoci al punto 1 se si ha l'accoppiamento perfetto tra le bobine ed il flusso ɸ concatena perfettamente entrambe le bobine avremo per la legge di Lenz sul circuito primario (N₁ spire): 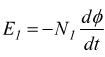   in modo analogo al secondario (N₂ spire): 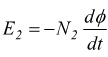     poi dividendo membro a membro le due equazioni:

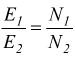
Per il punto 4 si ha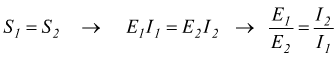  
Chiamato m il rapporto fra il numero di spire si ha:

       

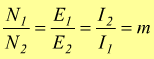
Adattamento di impedenza

      

Particolare importanza riveste il trasformatore nella questione dell'adattamento di impedenza tra un generatore ed un carico.

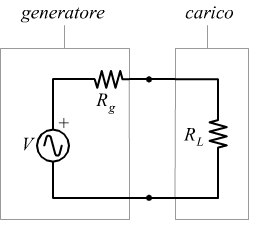
in tal caso, si può dimostrare che il massimo trasferimento di potenza tra generatore ed utilizzatore si ha quando la resistenza del generatore R_g è uguale al carico R_L.

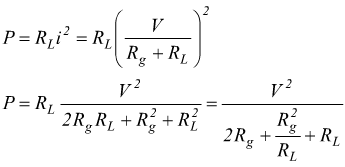
la potenza trasferita P è massima quando è minima.
Fissata (costante) R_g la funzione assegnata è minima rispetto alla variabile R_L quando la sua derivata prima si annulla :

   viene soddisfatta, appunto, per R_g=R_L.

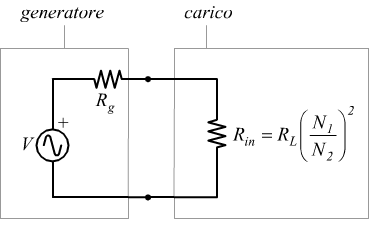
Se il carico ed il generatore sono separati da un trasformatore si ha la seguente situazione

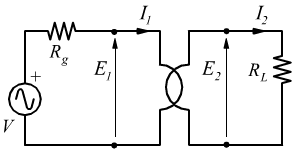
In tal caso la resistenza di ingresso vista a valle del generatore è R_in=E₁/I₁.

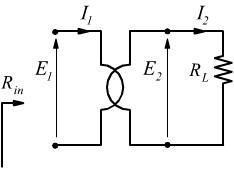
calcoliamo tale valore partendo dalle uguaglianze

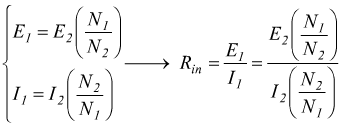
ma E₂=R_LI₂ dunque

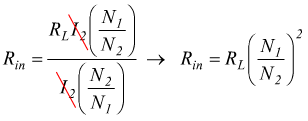
dove R_in è la resistenza di carico così come viene vista dal generatore. Si conclude che si possono adattare le impedenze di due apparati accoppiandoli con un trasformatore che abbia un opportuno rapporto di trasformazione m tale che possa porsi R_g=R_in , riuscendo in tal modo ad ottenere il massimo trasferimento di potenza.

Trasformatore monofase reale (caratteristiche)

      

1] Gli avvolgimenti presentano sempre una resistenza.
2] Il flusso magnetico non concatena perfettamente i due avvolgimenti.
3] La corrente magnetizzante non è trascurabile.
4] Vi sono perdite nel ferro dovute ad isteresi e a correnti parassite.



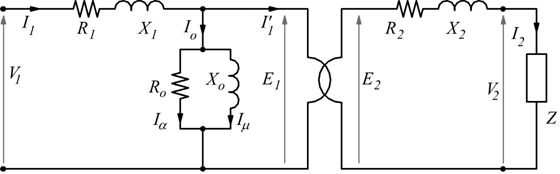
R₀: Resistenza che tiene conto delle perdite nel ferro per isteresi e per correnti parassite.
X₀: Reattanza induttiva che tiene conto della corrente magnetizzante necessaria a creare il flusso: coincide con l'induttanza dell'avvolgimento primario.
R₁ R₂: Resistenze che tengono conto delle perdite per effetto Joule negli avvolgimenti di rame primario e secondario.
X₁ X₂: Induttanze che tengono conto del flusso disperso negli avvolgimenti primario e secondario.

Prova a vuoto

      

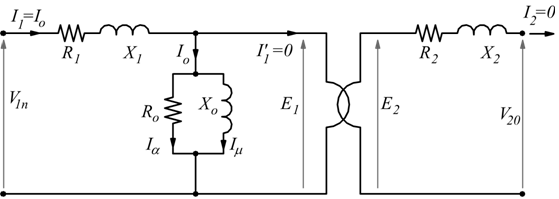
La prova a vuoto si effettua lasciando aperti i morsetti del secondario ed alimentando il primario alla tensione nominale V_1n.
Dato che il secondario è aperto, nella prova a vuoto si ha I₂=0 e dato che:
       
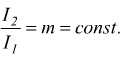
deve necessariamente essere I'₁=0, l'unica corrente circolante è I₀.
Non essendoci una corrente circolante nel secondario, tutta la potenza attiva assorbita dalla macchina è associata al circuito primario e vale:

dato che I_o << I_1n possiamo trascurare P_Cu0=perdite nel rame a vuoto rispetto a
P_f=perdite nel ferro quindi:

A vuoto la tensione ai capi del primario è V_1n ai capi del secondario è V₂₀: Viene definito il
rapporto di trasformazione a vuoto K_o:

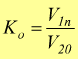       se il trasformatore è ideale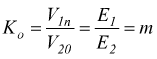           

A vuoto, il circuito secondario è aperto e non vi sono potenze erogate; formalmente è:

         

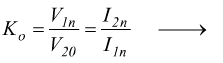
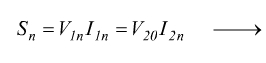
Il trasformatore assorbe dalla rete di alimentazione le potenze a vuoto

               

che possono anche essere ottenute tramite le relazioni

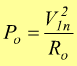
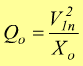                             Vengono poi definite:

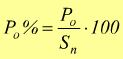          Potenza attiva percentuale a vuoto.

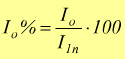          Corrente a vuoto in percentuale. Si ha poi:

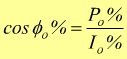          infatti:

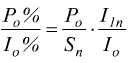
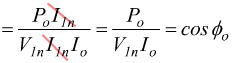
Variazione di tensione da vuoto a carico

      

Quando il trasformatore passa dal funzionamento a vuoto a quello sotto carico si ha una variazione della caduta di tensione sul circuito secondario.


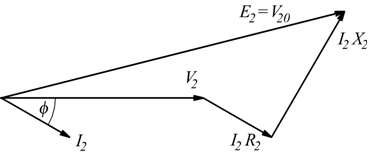
      caduta di tensione industriale

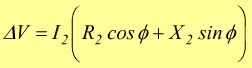
Circuito equivalente semplificato

      

I parametri caratteristici di un trasformatore reale sono noti solo al costruttore, nella pratica è impossibile risalire ad essi ma non è nemmeno indispensabile perché ai fini pratici, per lo studio delle grandezze elettriche ai capi dell'impedenza di carico, interessa solo la maglia secondaria. Come nel caso del trasformatore ideale è possibile adottare il seguente circuito equivalente:

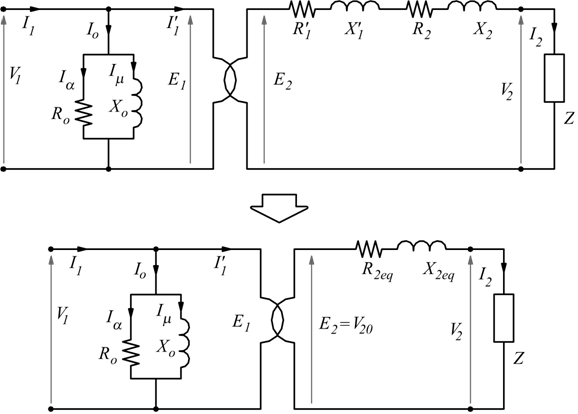
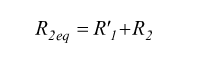
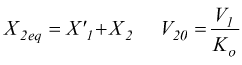
In questo modello si nota come sia E₁=V_1n

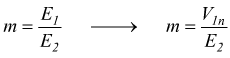
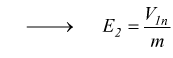
in questo circuito, durante il funzionamento a vuoto si ha:

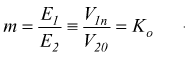
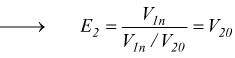
se si usa questo modello la formula per il calcolo della variazione di tensione da vuoto a carico si può usare:

Prova in corto circuito

      

La prova in corto circuito, si realizza cortocircuitando il secondario ed alimentando il primario con la tensione ridotta V_1cc, tale da far circolare nel secondario la corrente nominale I_2n.
Con tale tensione ridotta si assume I_o=0.

Da notare come in queste condizioni il primario sia percorso dalla I_1n.Le relazioni fondamentali sono:

Poi si ha:

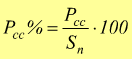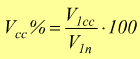          Potenza attiva percentuale in corto circuito.

       Tensione percentuale in corto circuito.

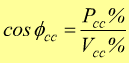        cosf percentuale in corto circuito. Infatti:



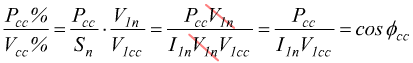
Da notare come, se il secondario è percorso da I_2n il primario debba sempre essere percorso da I_1n.

Rendimento

      

Il rendimento di una macchina è definito come il rapporto tra la potenza attiva in uscita (P₂) e la potenza attiva in ingresso (P₁).

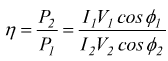
Vi sono delle oggettive difficoltà ad usare questa formula; gli strumenti di misura possono falsare questo rapporto in maniera significativa. Normalmente si usa:

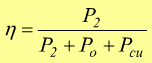           con: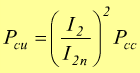          

P_o=Potenza attiva a vuoto
P_cu=Perdite nel rame
nella precedente si è indicato:             

in modo analogo si avrebbe:                

E' possibile, inoltre dimostrare:


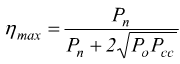
P_n=Potenza attiva nominale
P_o=Potenza attiva a vuoto
P_cc=Potenza in corto circuito con :