Corrente elettrica
Una corrente elettrica è composta da un flusso di particelle cariche o ioni. Per ottenere una corrente elettrica occorre applicare un campo elettrico in modo da far muovere le particelle cariche in una direzione ben definita.
L'intensità della corrente elettrica viene definita come la carica elettrica che passa nell'unità di tempo attraverso una sezione di regione in cui la corrente stessa fluisce (ad es. un filo metallico).
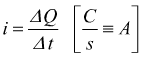 corrente
media
corrente
media
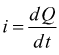 corrente
istantanea
corrente
istantanea
La corrente elettrica viene espressa i coulomb/secondo $$[\;C/s\;]$$, unità di misura che viene detta ampere [A]. Un ampere è l'intensità di una corrente elettrica corrispondente alla carica di un coulomb che passa attraverso la sezione del materiale ogni secondo.
Si assume convenzionalmente che la direzione di una corrente sia quella del moto delle particelle con carica positiva.
E' la stessa direzione del campo elettrico applicato o della caduta di potenziale che produce il moto delle particelle cariche, come mostrato nel seguente disegno dove con E si indica il campo elettrico e con i la corrente elettrica.
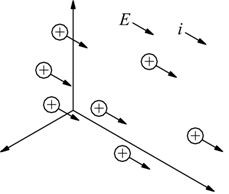
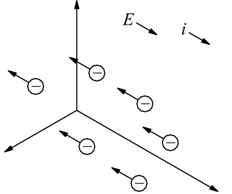
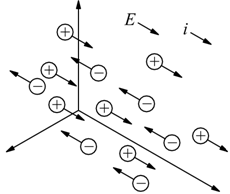
Quindi, se una corrente è dovuta al moto di particelle con carica negativa, come gli elettroni, la direzione convenzionale della corrente è opposta al moto reale degli elettroni.
Correnti elettriche e campi magnetici
Dato che la corrente elettrica è un flusso di cariche elettriche, quando un conduttore percorso da una corrente elettrica viene posto in un campo magnetico, esso è soggetto ad una forza perpendicolare alla corrente, che è la risultante delle forze magnetiche esercitate su ciascuna delle cariche in moto
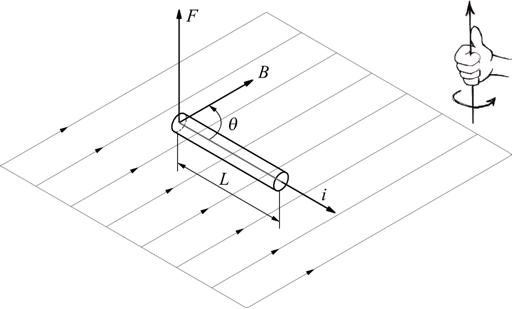
Mettendo il conduttore in diverse posizioni, con correnti e lunghezze differenti si ottiene sperimentalmente che il modulo della forza megnetica cui è soggetto il conduttore:
![]()
dove θ è l'angolo fra il conduttore e il campo magnetico.
La forza è nulla se il conduttore è parallelo al campo ( $θ=0$)
è massima se il conduttore è perpendicolare ad esso $$( θ=π/2
)$$. Quanto detto viene riassunto nella forma vettoriale:
![]()
dove $L↖{→}$ è un vettore che ha la lunghezza del filo rettilineo e il verso coincidente con quello della corrente i.
La formula precedente può anche essere ottenuta basandosi sulla la forza
di Lorentz agente su un singolo elettrone di carica elementare q=1,6×10-19C.
Supponiamo per semplicità che il conduttore ed il campo magnetico sia perpendicolari
tra loro, risulterebbe (sin90°=1) quindi la forza su di esso sarebbe
![]()
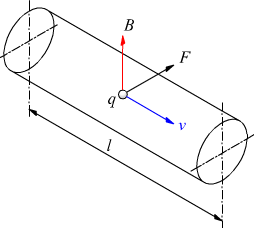
poi ipotizziamo che un tratto di conduttore l venga percorso da un elettrone di carica q in un tempo t con velocità v
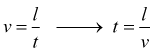 per
definizione, la corrente elettrica sarà in questo caso
per
definizione, la corrente elettrica sarà in questo caso
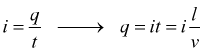
La forza di Lorentz per un elettrone che si muove con velocità perpendicolare al campo magnetico è
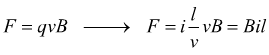
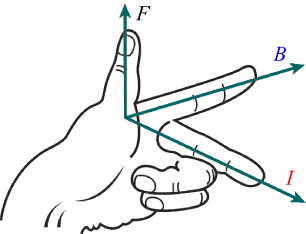
Alla forza di Lorentz viene sempre associata un'imortante regola mnemonica: la regola della mano sinistra, dove il dito pollice, l'indice e il medio sono ricondotti all'orientamento dei tre vettori $F↖{→}$, $B↖{→}$, i$L↖{→}$.
Campo magnetico prodotto da una corrente
Per primo H.C.Oersted si accorse, nel 1820, di come l'ago di una bussola
posta in vicinanza di un conduttore percorso da corrente elettrica,
subisse delle inaspettate deflessioni.
Ne dedusse che la presenza di cariche elettriche in movimento produce
un campo magnetico.
Dopo molti esperimenti eseguiti durante un periodo di vari anni, A.M.Ampère
e P.Laplace arrivarono empiricamente ad una equazione generale per calcolare
il campo magnetico prodotto da una corrente elettrica. Questa equazione
è detta di Ampère-Laplace:
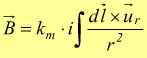
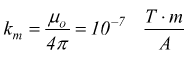
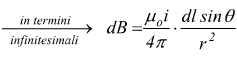
Secondo questa legge, il piccolo elemento di conduttore dl percorso dalla corrente i dà un contributo pari a dB al campo magnetico nel punto P che si trova ad una distanza r dal conduttore dl.
Questo contributo è perpendicolare al piano definito dai due
versori ![]() radiale e
radiale e ![]() tangenziale
al conduttore dl.
tangenziale
al conduttore dl.
Il termine µo è una costante fisica chiamata permeabilità magnetica del vuoto, dove appunto
Campo magnetico generato da una corrente rettilinea
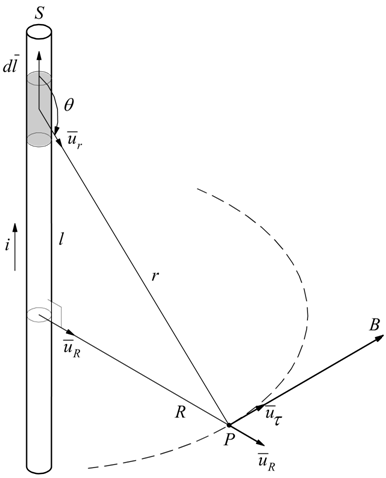
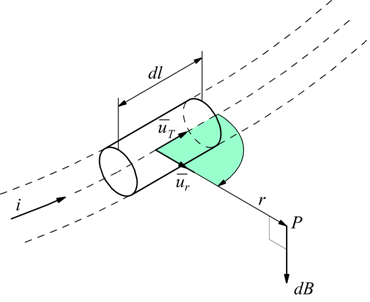
Nello schema disegnato per un qualsiasi punto P e per qualsiasi elemento dl ( che essendo un differenziale è arbitrariamente piccolo ) il vettore
$$dl↖{→}×du↖{→}_r$$
è normale al piano determinato da P e dalla corrente i, quindi
la sua direzione è quella del versore $u↖{→}_r$.
Il campo magnetico nel punto P, prodotto da $dl$ è
quindi tangente al cerchio di raggio R passante per P centrato
sulla corrente ed è in un piano perpendicolare alla corrente.
Quando si esegue l'integrazione della formula di Ampère-Laplace
si nota che i contributi di tutti i termini hanno la stessa direzione
di $u↖{→}_r$ ed
il campo magnetico è di conseguenza tangente al cerchio.
Quindi è sufficiente trovare i vari moduli, osservando che.
![]()
Per una corrente su un filo rettilineo di lunghezza infinita
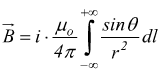
Dal disegno si riconosce  poi
osservando che
poi
osservando che
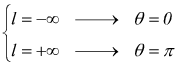 si
ricava
si
ricava
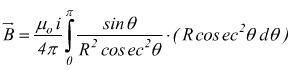
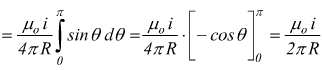
quindi per un conduttore rettilineo si ha 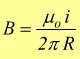
che come si nota è indipendente dalla lunghezza del conduttore.
Campo magnetico prodotto da una corrente circolare
Se ur è il versore ( vettore di modulo unitario ) per la direzione
AP.
Per una corrente circolare il vettore prodotto $dl↖{→}×u↖{→}_r$ è
perpendicolare al piano PAA' e ha modulo dl perchè i due vettori sono perpendicolari;
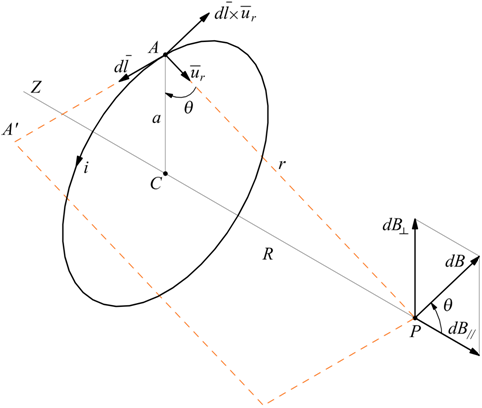
quindi il campo magnetico prodotto dall'elemento di lunghezza dl nel punto P ha modulo

questo elemento è perpendicolare al piano PAA' ed è quindi obliquo rispetto
all'asse Z se si scompone dB in una componente parallela $dB_{∥}$ e
in una componente perpendicolare $dB_{⊥}$, si
vede che l'integrazione da eseguire sul percorso circolare, per ogni $dB_{⊥}$ c'è
un'altra componente uguale e contraria, a causa dell'elemento diametralmente
opposto all'elemento dl.
Su come due elementi infinitesimi dl' e dl", opposti
fra loro, si comportano, può essere schematizzato nel modo seguente:
La somma algebrica delle componenti è zero. il campo B risultante deve essere la somma dei vari dB|| quindi collineare all'asse Z del cerchio. Notando che θ=a/r.
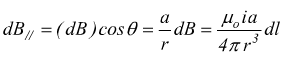
Nell'integrazione è r=cost. mentre per il cerchio  si
ha
si
ha
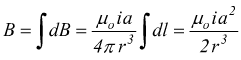 osservando
che
osservando
che ![]()
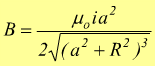 in
particolare al centro del cerchio si ha R=0
in
particolare al centro del cerchio si ha R=0 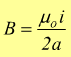
Se ragioniamo in esclusivamente in piano ci può anche essere un altro approccio; sempre partendo dalla formula di Ampère-Laplace
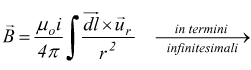
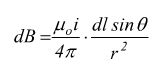
con θ angolo tra il versore uT pertinente alla direzione del conduttore dl ed il versore ur relativo alla direzione del segmento r che indica la distanza del conduttore dal punto in cui si sta valutando il campo magnetico. Se θ è sufficientemente piccolo si può approssimare θ=90° → sinθ=1.
dunque 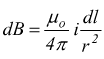
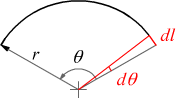
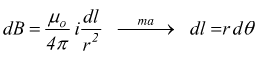
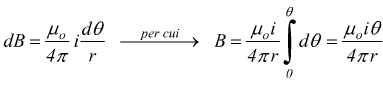
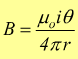 al
centro dell'arco
al
centro dell'arco
Legge di Ampère per il campo magnetico
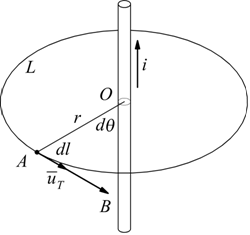
Consideriamo un conduttore rettilineo di lunghezza infinita percorso
da una corrente i.
Il campo magnetico B nel punto A a distanza r dalla corrente è perpendicolare
ad OA ed è dato dalla relazione
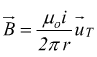
con uT versore tangente al cerchio di raggio r.
Calcoliamo la circuitazione 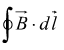
dove dl è un elemento infinitesimo di arco intorno alla corrente sul percorso
circolare di raggio r.
Dato che si tratta di un prodotto scalare e che B è tangente al percorso
![]()
mentre B è costante in modulo intorno al percorso circolare.
Si ottiene la circuitazione cercata, indicata come forza magnetomotrice
( fmm ).
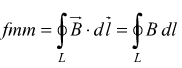
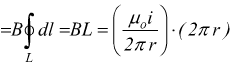 quindi
quindi
La circuitazione del campo magnetico ( o fmm ) lungo una linea chiusa che concatena la corrente i vale

chiaramente se il percorso concatena più correnti, la corrente i sarà rappresentativa della somma algebrica di queste correnti.
Non essendo nulla la circuitazione del campo si deduce che il campo magnetico non è conservativo, al contrario del campo elettrico e del campo gravitazionale che invece sono campi conservativi.
Campo magnetico di un solenoide
Un caso particolare di correnti circolari è quello degli avvolgimento o bobine o solenoidi che sono dispositivi composti da numerose spire coassiali tutte dello stesso raggio e tutte percorse dalla stessa corrente.
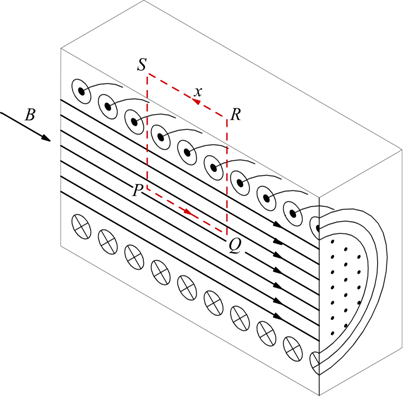
Consideriamo il solenoide disegnato che ha n spire per ogni unità di lunghezza percorse da una corrente i.
Se il solenoide è molto lungo e le spire sono molto compatte fra loro il campo magnetico è completamente confinato all'interno del solenoide; questo discorso non vale se vi sono delle dispersioni non trascurabili del campo all'esterno.
Applicando la legge di Ampère per il percorso chiuso SPQR osservando che per i lati QR ed SP si ha un contributo nullo dato che essi sono perpendicolari al campo. Per il lato SR non vi è nessun contributo perchè come detto all'esterno non c'è campo.
Solo il lato PQ contribuisce alla circuitazione con la quantità Bx.
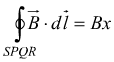 la
quantità di spire nella distanza x vale nx.
la
quantità di spire nella distanza x vale nx.
![]()
Avendo considerato n il numero di spire per unità di lunghezza se il solenoide è lungo L ed è costituito da un numero N di spire si ha
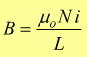 mentre
agli estremi il valore è la metà di quello al centro, cioè
mentre
agli estremi il valore è la metà di quello al centro, cioè 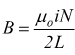
E' normale che il campo magnetico agli estremi sia la metà di quello al centro. Se un solenoide lungo viene diviso in due metà, il campo magnetico all'estremo comune è la somma dei campi prodotti dalle due sezioni. Pertanto ognuno deve essere metà del valore originario.
Le relazioni, confermano il fatto che all'interno del solenoide il campo magnetico è uniforme.
Campo magnetico di un avvolgimento toroidale
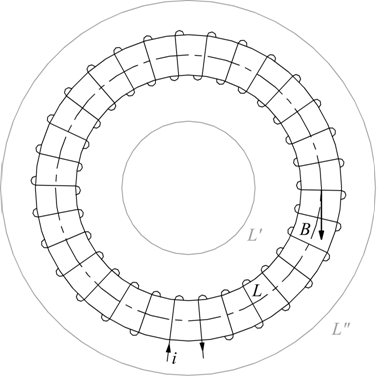
Un avvolgimento toroidale è fatto con un filo avvolto su un toro o superficie a forma di ciambella.
Si ipotizza che l'avvolgimento sia costituito da N spire percorse da una corrente i.
Se non vi sono dispersioni di campo all'esterno del toro, applicando la legge di Ampère al percorso L interno al toro, la circuitazione magnetica fornisce BL.
Il percorso L concatena tutte le N spire per cui la corrente che lo attraversa è NI, si ha dunque
![]()
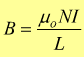
Forze fra correnti elettriche
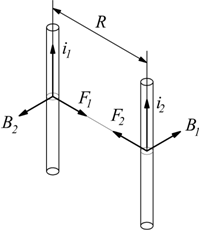
Visto che una corrente elettrica produce un campo magnetico che a sua volta esercita forze su altre correnti elettriche circostanti, si intuisce come possano verificarsi azioni meccaniche fra correnti elettriche. Il caso più semplice è dato da due correnti rettilinee e parallele i1 e i2.
il campo magnetico di i su i2 è dato da
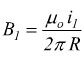
con la direzione indicata nel disegno.
La forza F2 su i2 è data dalla
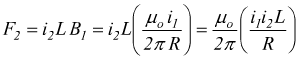 quindi
in generale
quindi
in generale
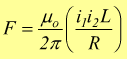
La forza sarà attrattiva se le due correnti hanno verso concorde, la forza sarà repulsiva se il verso delle correnti è discorde
Coppia magnetica e meccanica su una corrente elettrica chiusa
La forza esercitata da un campo magnetico su un circuito elettrico può dar luogo anche ad una coppia meccanica τ ed a una coppia magnetica M.
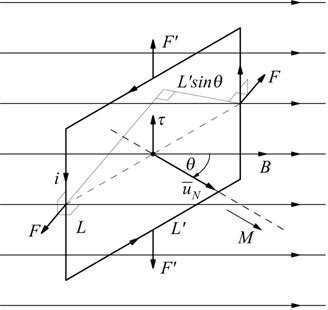
Nel disegno un circuito rettangolare percorso dalla corrente i, è posto in un campo magnetico uniforme B.
Il circuito è disposto in modo tale che il versore normale al suo piano uN ( orientato secondo la regola della mano destra ) formi un angolo θ col campo magnetico B.
Per i due lati L' perpendicolari al campo le forze F' che si esercitano su di loro, sono uguali e contrarie; sicuramente tenderanno a deformare il circuito, ma non producono nessuna coppia perchè giacciono nel piano del circuito.
Le forze F sui due lati L sono di modulo F=BiL e costituiscono una coppia
di braccio L'sinθ : esercitano un momento sul circuito che tende
ad orientare il circuito perpendicolarmente al campo magnetico.
Il modulo di questa coppia vale
![]()
poi notiamo che LL'=S superficie della spira; si ha quindi
![]()
La direzione del momento τ è perpendicolare al piano di forze F che lo generano. Si può ora, definire il vettore
![]() Momento
di dipolo magnetico [Am2]
Momento
di dipolo magnetico [Am2]
perpendicolare al piano del circuito, riscrivendo il momento meccanico come:
![]() esprimendolo
in forma vettoriale come
esprimendolo
in forma vettoriale come
![]()
Un circuito in un campo magnetico, è soggetto ad una coppia di forze che tendono ad orientare il momento di dipolo magnetico del circuito parallelamente al campo.
| 0° |
 edutecnica
edutecnica