Criterio del luogo delle radici

      

Il metodo del luogo delle radici ( Evans 1948 ) è a tutt'oggi il metodo più rigoroso per valutare la stabilità di un sistema reazionato, partendo dalla conoscenza dei poli e degli zeri della funzione di trasferimento ad anello aperto G_loop=A(s)B(s).
Ricordando che per un sistema reazionato, la funzione di trasferimento ad anello chiuso vale .

i poli della funzione di trasferimento ad anello chiuso si ottengono determinando le radici del denominatore della funzione stessa

Considerando la funzione ad anello aperto posta in prima forma canonica:

          [I]

si ha di conseguenza

                                          [II]

L'argomento della [I] è la somma algebrica dei singoli vettori ( positivi quelli degli zeri negativi quelli dei poli ), il modulo della [I] è ottenibile facendo il prodotto dei moduli dei vettori relativi agli zeri diviso il prodotto dei moduli dei vettori relativi ai poli col risultato moltiplicato per k_o.

Ora perchè un punto del piano complesso sia una radice della [II] serve che la somma algebrica degli argomenti dei vettori sia pari a 180°+h360° h∈N e che il prodotto dei moduli dei vettori relativi agli zeri diviso il prodotto dei vettori dei poli sia uguale a 1/k_o.

Escludendo una ricerca per tentativi dei valori della variabile s che soddisfi a questi requisiti si può invece pensare, di trovare tutti i punti del piano complesso che soddisfino la relazione angolare: somma algebrica degli argomenti=180°+h360°. Questi punti stanno su delle curve che possono essere ricavate attraverso delle precise regole.

Queste curve rappresentano il luogo delle radici dato che le eventuali radici della [II] possono trovarsi su queste curve.

Si definisce il luogo delle radici, l'insieme di curve nel piano complesso i cui punti possono essere i poli del sistema reazionato.

In pratica, il luogo delle radici si compone di diversi rami e per un dato valore di k_o su ogni ramo esiste una radice; per cui i rami sono tanti quante le radici della [II].

Una volta tracciati i luoghi delle radici, invece che cercare per tentativi i punti che soddisfano alla relazione del modulo, conviene 'tarare' i luoghi in funzione di k_o. infatti dalla [II] mettendo in modulo entrambi i membri

In base a quest'ultima equazione si deve avere una esatta visione di come variano i poli del sistema reazionato in funzione della variazione del guadagno statico d'anello k

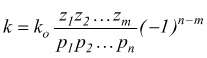
Essendo il luogo delle radici rappresentativo della collocazione dei poli della funzione di trasferimento ad anello chiuso G(s) è evidente che i valori di k_o per i quali il luogo delle radici si addentra nel semipiano destro rendono il sistema instabile.

1) Numero dei rami.
Il numero dei rami del luogo delle radici è uguale al numero dei poli della funzione di trasferimento ad anello aperto.

2) Partenza dei rami.
I rami del luogo delle radici partono dai poli della funzione ad anello aperto.

3) Arrivo dei rami.
I rami del luogo delle radici terminano negli zeri della funzione di trasferimento ad anello aperto, oppure all'infinito.

4) Simmetria rispetto all'asse reale.
Il luogo dele radici è simmetrico rispetto all'asse reale.

5) Luogo delle radici sull'asse reale.
Sull'asse reale il luogo delle radici è costituito da tutti quei punti tali che il numero dei poli e degli zeri alla loro destra sia dispari.

6) Direzione degli asintoti.
I rami del luogo delle radici che terminano all'infinito tendono a degli asintoti i cui coefficienti angolari sono dati dalla relazione

dove n è il numero di poli ed m è il numero degli zeri della funzione G_loop=A(s)B(s).
Dato che h può assumere qualsiasi valore intero, potrebbe sembrare che ci siano infiniti asintoti; in realta questi risultano pari ai rami che vanno all'infinito, dato che al crescere di h i valori di α si ripetono . Ad es. i valori di α in funzione di n-m sono:

n-m	α
1	180°
2	90° | 270°
3	60° | 180° | 300°
4	45° | 135° | 225° | 315°

7) Intersezione degli asintoti.
Gli asintoti incrociano l'asse reale in un punto di ascissa data dalla relazione

8) Punti di biforcazione dall'asse reale.
Il punto o i punti in cui i rami del luogo delle radici si distaccano dall'asse reale è determinato uguagliando a zero i reciproci delle distanze dei poli e degli zeri reali da quel punto. Questo viene espresso dalla relazione:

9) Direzione di partenza e di arrivo dei luoghi.
I rami del luogo che partono dai poli complessi coniugati lasciano tali punti con un angolo θ rispetto alla direzione dell'asse reale dato dalla relazione:

Dove θ_i è l'argomento del vettore congiungente lo zero z_i con il polo considerato e φ_i è l'argomento del vettore congiungente il polo p_i con il polo considerato.
In modo analogo si può dimostrare che i rami che giungono agli zeri complessi coniugati arrivano con un angolo θ rispetto all'asse reale dato da:

10) Somma delle parti reali delle radici.
Nel caso che il grado del denominatore della G_loop=A(s)B(s) superi di almeno 2 quello del numeratore
( n-m≥2 ) la somma delle parti reali delle radici della funzione di trasferimento ad anello chiuso risulta costante,indipendentemente dal valore di k_o.

Esempio 1

          con        

si ha un solo polo per       .

Il luogo delle radici ha un solo ramo che coincide con l'asse reale negativo a sinistra di ;
il ramo termina a ; non essendovi zeri.

     per s=–2 si ha

per s=–4 si ha

Esempio 2

   con   

Per la regola 1 il luogo consiste in due rami che partono dai poli p₁=-1 e p₂=-10 che terminano all'infinito non essendovi zeri.

Per la regola 5 appartiene al luogo delle radici il tratto dell'asse reale compreso fra i due poli.
I due rami terminano all'infinito per la regola 6 formando con l'asse reale angoli di 90° e 270° ( n-m=2 ) ed incontrano l'asse delle ascisse nel punto dato dalla regola 7.

I due rami si distaccano dall'asse reale nel punto di ascissa a data dalla regola 8.

dunque a=d :si nota che questo punto coincide con quello di incontro degli asintoti, quindi in questi tratti il luogo delle radici coincide con gli asintoti stessi.

nel punto a=-5,5 si ha                    

nel punto b=-5,5+j2 si avrebbe     

Esempio 3

    con     

I base alla regola 1 il luogo è costituito da due rami di cui uno termina nello zero ( regola 3 ) e uno all'infinito con asintoto a 180° in base alla regola 6. Il luogo è dunque costituito da due tratti sull'asse reale determinati in base alla regola 5 ed è disegnato come:

Esempio 4

    con    

Se ci sono tre poli, il luogo delle radici deve avere tre rami che partendo da dai poli devono terminare all'infinito non essendoci zeri. Appartengono all'asse reale i tratti compresi tra -0,25 e -0,5 (un polo a destra ) e a sinistra dal punto -1 (tre poli a destra ). Per la regola 6 si hanno tre asintoti con inclinazione 60°;180° e 300° che si incontrano sull'asse reale nel punto di ascissa dato dalla regola 7

Il luogo delle radici si stacca dall'asse reale in un punto d dato dalla relazione

( la seconda soluzione –0,8 non appartiene al luogo delle radici ) .
Campionando alcuni valori che appartengono al luogo troviamo

s	ko
-0,4+j0	0,009
-0,43+j0	0,00718
-1,018+j0	0,00716
0,363+j0	0,01
0,3±j0,27	0,57
-1,126+j0	0,56
-0,2±j0,535	2,53
0±j0,9,35	11,25
0,215±j1,315	30
-2,17+j0	30

è possibile controllare i risultati ottenuti con questa pagina.

In particolare l'attraversamento dell'asse immaginario che indica il limite della stabilità può essere individuato in due modi:
1) tramite il criterio di Routh
2) ponendo s=jω nell'equazione caratteristica

1+A(s)B(s)=0

e risolvendo il sistema

che a volte può essere laborioso; ad es. nel nostro caso:

uguagliando a zero la parte immaginaria

uguagliando a zero la parte reale e sostituendo