Stabilità

      

Quando un sistema è soggetto ad un segnale perturbatore, esso, può veder evolvere il proprio assetto; se al cessare del segnale perturbatore il sistema torna nelle sue condizioni inziali i sistema viene detto stabile.
Il sistema è' invece instabile quando si allontana definitivamente dalle condizioni iniziali.
Un esempio di sistema stabile è dato da una pallina vincolata a muoversi su una curva contenuta in un piano verticale con la concavità verso l'alto.

Supponendo che in condizioni di riposo la pallina si trovi nel punto 0, se a questa viene applicata una forza impulsiva (spinta) in grado di spostarla da tale posizione, al cessare della perturbazione la pallina, dopo un certo numero di oscillazioni di ampiezza via via decrescente a causa dell'attrito, ritornerà nella condizione iniziale.

Se invece la pallina è vincolata a muoversi su una curva con la concavità rivolta verso il basso, supponendo che la pallina sia in equilibrio inizialmente nel punto 0, applicando una forza impulsiva tale da spostarla anche solo leggermente, una volta lasciata la posizione iniziale, cade lungo la curva a cui è vincolata, senza più ritornare nella posizione di partenza. Nel primo caso il sistema è stabile,nel secondo è instabile.
La stabilità di un sistema può essere studiata esaminando la funzione di trasferimento complessiva del sistema G(s). Infatti si può pensare di applicare al sistema un segnale perturbatore costituito da un impulso unitario ed esaminare la sua risposta nel tempo.

Supponendo inizialmente il sistema in condizioni di riposo, con uscita nulla, se esso è stabile, la risposta all'impulso unitario (delta di Dirac) deve tendere a zero, mentre se è instabile diverge.

Nella pratica la risposta di un sistema instabile non assume mai valori infinitamente grandi, perché intervengono delle non linearità che delimitano l'ampiezza della risposta dell'uscita.

Siccome la trasformata di Laplace di un impulso unitario (impulso deltiforme di durata nulla ampiezza indefinita e area unitaria) vale 1, la risposta del sistema a tale perturbazione si ottiene eseguendo l'antitrasformata della funzione di trasferimento G(s).

Si dispone la funzione di trasferimento del sistema nella sua prima forma canonica

poi, la si decompone in frazioni parziali tramite lo sviluppo di Heaviside

dove i poli p₁,p₂..p_n possono essere reali o complessi coniugati.
Nel caso di poli reali, si ha dalla tabella delle antitrasformate che il per il generico termine

questo termine tende a zero per t → ∞ solo se p è negativo mentre se p > 0 tale termine tende ad ∞.
Nel caso si trovino dei poli complessi coniugati del tipo

Nella scomposizione in frazioni parziali della G(s) si trovano termini del tipo

che poi possono essere riuniti in un unico termine

che antitrasformata risulta essere

Se la parte reale k è negativa l'espressione precedente è rappresentata da sinusoidi smorzate che per t → ∞ tendono a zero; se k è positiva queste sinusoidi sono di ampiezza crescente e tendono ad una ampiezza infinita per t → ∞

Da quanto visto: è condizione necessaria e sufficiente per la stabilità di un sistema lineare è che tutti i poli della funzione di trasferimento G(s) del sistema siano negativi se reali o che abbiano parte reale negativa se complessi coniugati. .

In pratica si rappresentano i poli del sistema sul piano complesso ; perché il sistema sia stabile, occorre che tutti i poli si trovino nel semipiano sinistro (parte reale negativa) . Basta che ci sia un solo polo nel semipiano destro (parte reale positiva) perché il sistema sia instabile.

Quindi per valutare la stabilità, non è necessario antitrasformare la funzione di trasferimento del sistema G(s) ma solo esaminare la posizione dei poli sul piano complesso.

Criterio Routh

      

Il criterio di Routh è un metodo matematico per stabilire se un polinomio di grado n ammette radici a parte reale positiva, senza risolvere l'equazione che si ottiene uguagliando a zero il polinomio, ma solo dall'esame dei suoi coefficienti. Va applicato al denominatore D(s) della funzione di trasferimento del sistema ( funzione di trasferimento ad anello chiuso ):

Consideriamo il polinomio di grado n

Dai teoremi dell'algebra si può dimostrare che, perché il polinomio abbia radici tutte negative, è necessario ma non sufficiente, che i coefficienti a_o a₁ a₂..a_n abbiano tutti lo stesso segno e che nessuno di essi sia nullo. Accertata tale condizione, si può calcolare la tabella di Routh disponendo i coefficienti su due righe prendendoli in ordine alterno.

La terza riga viene formata con i termini delle prime due righe prendendoli in ordine alterno: secondo la regola:

                       etc..

si continua così finchè non si ottiene un termine x_i=0 compilando la tabella secondo l'orditura:

nel caso particolare di polinomi di grado 3 e 4

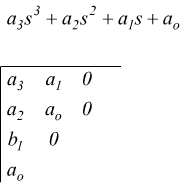
Il criterio di Routh afferma che un sistema è stabile se nella tabella non vi sono cambiamenti di segno nei numeri della prima colonna.

Architettura di sistemi

      

Supponendo di voler riempire un serbatoio di acqua fino ad un livello prefissato; oltre al serbatoio ci occorrerà una conduttura e una valvola (ON/OFF) attivabile tramite un comando (pulsante o manopola).

Il processo eseguito, consiste nel trasferimento della massa di liquido che riempie il serbatoio facendolo passare da un livello di partenza fino al livello desiderato. Un sistema di questo tipo, denominato a catena aperta richiede la presenza di un operatore che svolga una funzione di controllo e di regolazione . Ovviamente, come si è visto nel caso dei sistemi idraulici, ci sarà una funzione di trasferimento G(s) che descriverà il comportamento fisico del sistema che metterà in relazione una variabile di ingresso x (ad es. lo stato del comando) e una variabile di uscita y (ad esempio il livello del liquido nel serbatoio).

Un modo per migliorare l'efficacia del controllo e ridurre l'effetto di eventuali disturbi sul sistema è quello di utilizzare sistemi a catena chiusa,

dove ad esempio si misura il livello del liquido nel serbatoio e si attiva un'azione correttrice nel caso in cui il livello sia diverso dal valore desiderato.

L'anello di reazione disegnato in figura svolge questa funzione e consente la regolazione automatica del livello del serbatoio.
L'azione correttrice dipende dalla differenza tra il valore misurato e il valore atteso del livello del liquido.

Ai fini del controllo della grandezza di uscita si utilizza la retroazione negativa, perché questo tipo di reazione è meno sensibile alle variazioni parametriche, ha una maggiore immunità ai disturbi e permette di ottenere il valore atteso della grandezza controllata con un errore prefissato.
Vi sono anche degli svantaggi: il sistema è più complesso e sono necessari più componenti, si ha una diminuzione del guadagno rispetto alla condizione di anello aperto, possono instaurarsi condizioni di instabilità.
La retroazione positiva, implica invece che il segnale di reazione si sommi al segnale di ingresso introducendo una deriva che porta l'uscita verso una saturazione, perdendo di fatto il controllo del sistema.
Questa condizione di funzionamento è inaccettabile e il progettista deve accertarsi che non si verifichi mai.

Sistemi reazionati

      

Un generico sistema di controllo retroazionato è normalmente costituito da elementi di per sé stabili collegati fra loro in vari modi riducibili alla forma rappresentata nel disegno, con un blocco di andata A(s) è un blocco di reazione che ha funzione di trasferimento B(s).

Per poter esaminare la stabilità dell'intero sistema occorre calcolare la funzione di trasferimento complessiva E calcolarne i poli, oppure applicare il criterio di Routh. Nel primo caso si va incontro a calcoli laboriosi, mentre nel secondo caso non si hanno indicazioni sufficienti sul grado di stabilità del sistema.

I due metodi seguenti tendono ad evitare calcoli complessi determinando la stabilità del sistema partendo dall'esame della funzione di trasferimento ad anello aperto:

che si ottiene azzerando l'ingresso e tagliando in un punto qualsiasi l'anello di reazione. ad es. se si apre l'anello come indicato in figura e si immette con segnale di riferimento x nullo un segnale i(s) dall'altra parte del taglio si ottiene un segnale di uscita u(s) .

                                da cui si ottiene

                     funzione di trasferimento ad anello aperto

Il vantaggio di prendere in considerazione la funzione di trasferimento ad anello aperto è che per questa è relativamente facile calcolare poli e zeri in quanto derivante dalla riduzione di blocchi in cascata.
Metodi di analisi comunemente usati che usano la funzione di trasferimento ad anello aperto sono quelli di Nyquist e di Bode.

Criterio di Nyquist

      

E' un criterio di stabilità per sistemi reazionati e prende in considerazione il diagramma polare della funzione di trasferimento ad anello aperto A(jω)B(jω) con un segnale di ingresso di tipo sinusoidale. Esso si basa sul teorema di Cauchy sulle funzioni analitiche.

Se p è numero dei poli del guadagno dell'anello G_Loop a parte reale positiva, il sistema ad anello chiuso G(s) risulta stabile, se il diagramma di Nyquist della G_Loop=A(s)B(s) completo della sua parte speculare
( immagine della funzione per -∞ < ω < +∞ ) compie in senso orario un numero di giri n attorno al punto di coordinate (-1;0) pari al numero di poli p con parte reale positiva; cioè se n=p il sistema è stabile.

Spesso la G_loop=A(s)B(s) nel senso che non contiene poli a parte reale positiva, per cui p=0 e il criterio può essere enunciato attraverso la sua forma ridotta.

Se il sistema retroazionato è stabile ad anello aperto ( p=0 ) allora esso è tale anche ad anello chiuso se n=0; cioè il diagramma di Nyquist della G_Loop non deve contenere al suo interno il punto di coordinate ( -1;0 ).

Criterio di Bode

      

Il criterio di Bode non è altro che il criterio di Nyquist trasferito sui diagrammi cartesiani invece che su quelli polari. Si considera la funzione di trasferimento del sistema a catena aperta ( G_loop ).

Se abbiamo i diagrammi cartesiani occorrerebbe trovare sul diagramma della fase la pulsazione ω° a cui corrisponde uno sfasamento di 180° e in corrispondenza di ω° sul diagramma del modulo esaminare se la corrispondente attenuazione è maggiore o minore di 1 ovvero maggiore o minore di 0 dB.
Il più delle volte si dispone solo del diagramma del modulo e non è agevole determinare ω° allora si può osservare il diagramma polare.

Un sistema stabile non abbraccia il punto di coordinate ( -1, j0 ) del diagramma polare e appare normalmente come rappresentato in figura.
In tal caso un cerchio di raggio unitario con centro nell'origine taglia il diagramma nel punto T cui corrisponde una ω_T detta pulsazione di taglio; il vettore corrispondente ha modulo unitario e argomento φ_T minore di 180°.
Nel caso di un sistema instabile il sistema si presenta ,invece, come rappresentato nel secondo grafico.
Il diagramma abbraccia il punto di coordinate ( -1, j0 ) e il cerchio di raggio unitario taglia questa volta il diagramma polare in un punto T, in cui il vettore ρ presenta un argomento φ_T>180°.
Sul diagramma cartesiano il valore _T corrispondente all'attenuazione 1 ( 0 dB ) è quello in cui il diagramma cartesiano taglia l'asse 0 dB.
Basta allora calcolare lo sfasamento in corrispondenza del valore trovato.

Il criterio di Bode afferma che il sistema è stabile se lo sfasamento calcolato in corrispondenza della pulsazione di taglio è inferiore a 180°; è instabile se superiore a 180°.

Un'altra regola, più generale ( e grossolana ) consiste nell'osservare il diagramma del modulo della G_loop: se l'attraversamento dell'asse a 0 dB avviene con una pendenza di 20 dB/dec il sistema è stabile;
se la pendenza è maggiore o uguale a 40 dB/dec il sistema è instabile.

Margine di fase

      

Questo parametro fornisce una misura quantitativa del grado di stabilità di un sistema