Dinamica del moto rotatorio
Ipotizziamo che un solido cilindrico sia inizialmente fermo, ammettiamo
che esso abbia solo la possibilità di ruotare attorno al suo asse geometrico.
Supponiamo poi, che sia formato da un numero elevatissimo di piccoli
elementi di massa mi.
Applicando ad ogni singola massa una forza elementare piccolissima,
comunque orientata, ma non passante per
l'asse geometrico del cilindro, otteniamo infiniti momenti elementari
che possono produrre il moto di rotazione del cilindro.
Supponiamo per semplicità che le forze siano tutte dirette perpendicolarmente
al raggio del cilindro;

ogni massa elementare mi è messa in condizione di descrivere un moto circolare, uniformemente accelerato sotto l'azione della forza Fi cui è soggetta. Per ciascuna massa elementare, perciò, la seconda legge della dinamica
![]()
moltiplicando entrambi i membri per la distanza dal centro di rotazione
![]()
considerando la relazione cinematica a=α·r dove α è l'accelerazione angolare si ottiene
![]()
si vede che il primo membro è la risultante di tutti i momenti elementari dovuti alle singole forze, cioè il momento complessivo M che produce il moto di rotazione.
![]()
Mentre al secondo membro l'accelerazione angolare α è uguale per tutti punti del cilindro e dunque può essere portata fuori dal segno di sommatoria. Notiamo che quest'ultimo è rappresentativo del momento di inerzia di massa del cilindro J.
![]() si
ha dunque
si
ha dunque
![]()
quest'ultima è l'equazione fondamentale del moto rotatorio, analoga
alla relazione F=ma, vista nel caso dei moti traslazione.
Dalla formula si vede che a parità di momento motore applicato l'accelerazione
angolare α è tanto più elevata quanto minore è il suo momento
di inerzia di massa rispetto all'asse stesso. Se
il solido è di forma cilindrica il momento di inerzia è
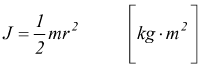
a parità di massa l'accelerazione acquisita è tanto maggiore quanto minore
è il raggio del cilindro;la sua lunghezza invece non ha nessuna influenza
sull'accelerazione.
Se vogliamo fermare un solido cilindrico in moto rotatorio, il momento resistente
da applicare deve essere tanto maggiore quanto più elevato è momento di
inerzia del cilindro.
A parità di momento resistente la decelerazione angolare è tanto più piccola
quanto più grande è il valore del momento di inerzia; quindi un corpo di
grande momento di inerzia per essere ricondotto alla quiete, impiega un
intervallo di tempo maggiore rispetto ai solidi con momenti di inerzia minori.
Sulla computazione del momento di inerzia per varie geometrie di corpi solidi avevamo già precedentemente annotato qualcosa, riassumiamo ulteriormente le principali tipologie.
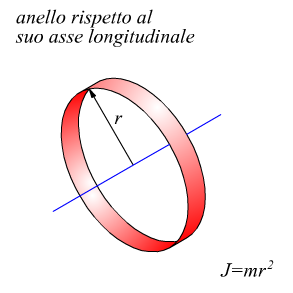
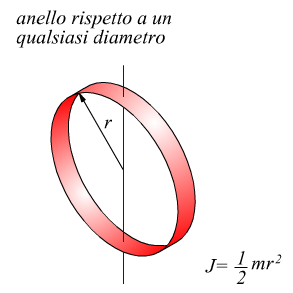
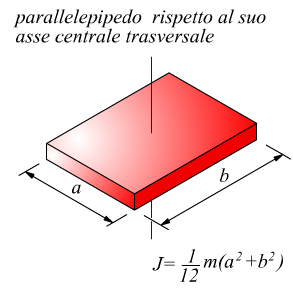
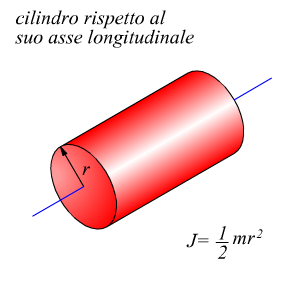
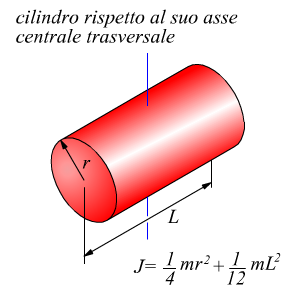
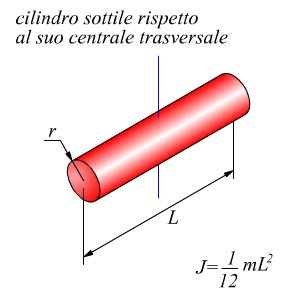
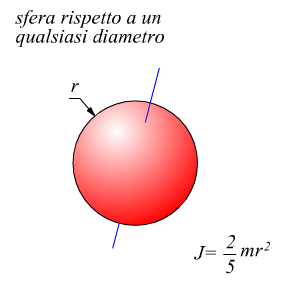
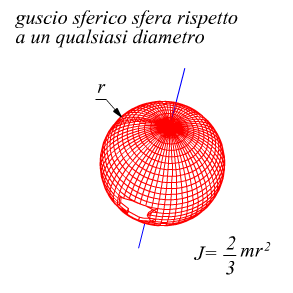
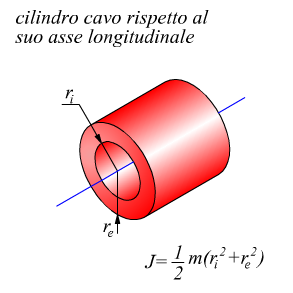
A tal proposito è necessario ricordare che anche se l'asse di rotazione assegnato non passa attraverso al centro di massa, rimane valido il principio di trasposizione di Huygens-Steiner valido per i momenti di inerzia di superfici:
![]()
dove d è la distanza perpendicolare tra l'asse di rotazione assegnato e l'asse parallelo passante per il centro di massa.
Teorema del momento della quantità di moto
Moltiplicando entrambi i membri dell'equazione fondamentale del moto rotatorio per il tempo
![]() dato
che
dato
che 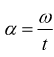 si
ha
si
ha
![]() analoga
al teorema della quantità di moto Ft=mv
analoga
al teorema della quantità di moto Ft=mv
M·t=L=momento dell'impulso
J·ω=momento della quantità di moto
Teorema del momento della quantità di moto:
il momento dell'impulso impresso al corpo è pari alla variazione del
momento della quantità di moto.
![]()
Il moto rotatorio, può dunque essere espresso dall'equazione
![]()
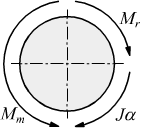
Dove M è la risultante dei momenti delle forze attive e reattive applicate al corpo e Jα può essere assimilato ad un momento fittizio che si oppone alla realizzazione del moto.
 Nel caso più
generale, il solido è soggetto a più di un momento a causa di eventuali
resistenze passive; se indichiamo
Nel caso più
generale, il solido è soggetto a più di un momento a causa di eventuali
resistenze passive; se indichiamo
Mm=momento motore
Mr=momento resistente
![]() se
risulta
se
risulta ![]()
il corpo in rotazione si ferma; visto che J≠0 deve essere α=0.
Questa conclusione ci riporta alla prima legge della dinamica già vista
per il moto traslatorio, che , in questo caso, può essere espressa come:
Un corpo persevera nel suo stato di quiete o di moto circolare uniforme fino a che non interviene una causa esterna (momento) ad alterare questo stato.
 Se viene ad
annullarsi il momento motore, la presenza del momento resistente Mr
tende a rallentare il moto del solido; la condizione di equilibrio dinamico
diventa
Se viene ad
annullarsi il momento motore, la presenza del momento resistente Mr
tende a rallentare il moto del solido; la condizione di equilibrio dinamico
diventa
![]()
con il momento dovuto all'inerzia del mobile( Jα) che cambia verso e si dispone in modo da opporsi all'effetto prodotto dal momento resistente: tende ad impedire il rallentamento del corpo.
Nel moto rotatorio, il prodotto J·α è l'equivalente della forza di inerzia m·a dei moti di traslazione; il prodotto J·α è la reazione inerziale opposta dal corpo alla variazione di velocità imposta dal momento applicato.
Come si vede dagli schemi, la componente di inerzia J·α , durante il moto, si oppone sempre alla risultante dei momenti attivi e resistenti.
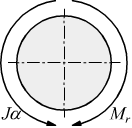
Nello schema successivo viene illustrato il comportamento di un solido
dotato di massa m e raggio r, soggetto ad un momento motore M e ad un
eventuale momento resistente Mr che riteniamo
costante durante tutto il funzionamento.
Ipotizzando un momento motore M=1Nm con un momento resistente Mr=20%
di M=0,2N, una massa m=3kg ed un raggio r=3m il momento totale agente
sarebbe
![]()
supponiamo di applicare il momento motore M per un tempo ta=9 sec.
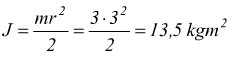
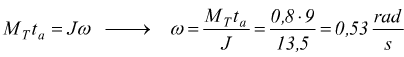 in
termini di giri al minuto sarebbero
in
termini di giri al minuto sarebbero
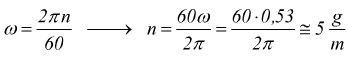
questa è la massima velocità angolare raggiunta, con una accelerazione angolare

Dopo l'istante ta=9sec viene a meno il momento motore rimane solo il momento resistente, così subentra una decelerazione
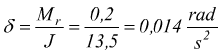 il
tempo impiegato a fermarsi è
il
tempo impiegato a fermarsi è 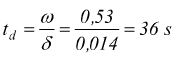
|
r : 1 m m : 1 kg M : 1.0 Nm Mr = 0% di M
|
|
Moto rototraslatorio
Nel caso di moto rototraslatorio, come ad es. quello di un rullo cilindrico su di un piano orizzontale privo di attrito occorre considerare simultaneamente l'equazione fondamentale del moto rotatorio con la seconda legge della dinamica; soltanto che la prima è un bilancio di momenti, la seconda un bilancio di forze. Dato che
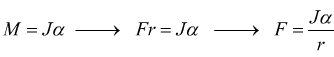
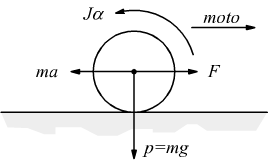
la seconda legge della dinamica, nel caso di moto rototraslatorio, deve essere corretta aggiungendo la forza di inerzia dovuta al moto rotatorio
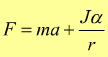
Questa correzione dovrebbe essere apportata anche in altri casi già visti. Ad es. la forza di inerzia del corpo rigido in rotazione, deve essere considerata anche nei problemi con la carrucola dove in genera si trascura Il momento di inerzia (la massa) di quest'ultima.
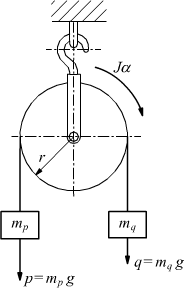
In genere indichiamo con mp ed mq le masse di
due corpi (mp>mq) collegati tra loro da una
fune inestensibile e di massa trascurabile avvolta per mezzo giro su
una puleggia.
Se indichiamo con mo la massa della puleggia e con r il suo raggio.
Lasciando contemporaneamente liberi i due corpi, il più pesante mp inizia un moto di discesa accelerato, trascinando l'altro di massa mq in moto ascendente, ponendo in rotazione la puleggia.
Trascurando la puleggia il problema sarebbe limitato a moti di semplice traslazione scrivendo
![]() ottenendo
ottenendo 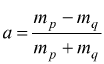 chiaramente
con a<g
chiaramente
con a<g
Tenendo conto dell'inerzia alla rotazione opposta alla puleggia, l'accelerazione acquisita dal complesso sarà prevedibilmente appena inferiore a quella appena calcolata. Se esprimiamo la condizione di equilibrio dinamico valutando i momenti delle varie forze rispetto al centro O della puleggia i singoli termini sono
momento motore ![]()
momento resistente ![]()
momento della forza di inerzia di ![]()
momento della forza di inerzia di ![]()
momento della forza di inerzia della puleggia ![]()
![]()
sapendo che 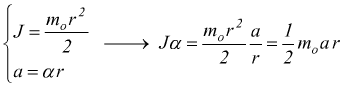 ottenendo
ottenendo
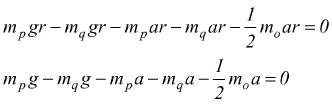
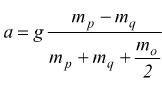
che differisce dalla precedente per il termine mo/2 al denominatore.
Energia
Nel caso di un corpo rigido che ruota attorno ad un asse con velocità angolare ω la velocità di ogni particella i-esima è vi=ωri con ri distanza della particella dall'asse di rotazione, allora
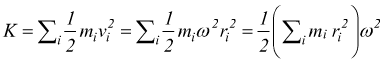
dato che prima abbiamo definito il momento di inerzia
![]()
possiamo allora ritenere che l'energia cinetica di un corpo che ruota attorno ad un asse sia
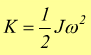
Consideriamo invece il caso più generale in cui un corpo rigido ruota per un asse passante per il suo centro di massa ed al medesimo tempo trasla rispetto ad un osservatore; dobbiamo sommare le due energie cinetiche : quella di traslazione e quella di rotazione ottenendo la seguente formula
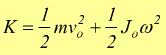
in questa equazione vo è la velocità del centro di massa (baricentro) del corpo mentre Jo è il momento di inerzia rispetto sempre al centro di massa del corpo, supponendo che per questo passi l'asse di rotazione.
In base al principio di conservazione dell'energia, possiamo assumere che l'energia totale posseduta dal corpo in rototraslazione sia

somma dell'energia cinetica e potenziale rimanga costante.
 edutecnica
edutecnica