La carrucola
La carrucola è una macchina semplice, infatti, per come è stata descritta in precedenza, è assimilabile ad una leva di primo genere
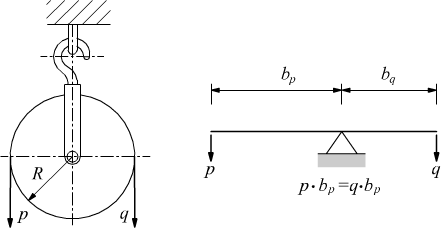
La differenza tra una leva ed una carrucola è che in quest'ultimo caso il braccio della forza motrice p e della forza resistente q è lo stesso (R) dunque:
![]()
non vi è alcun vantaggio nell'usare la carrucola, lo sforzo fatto è
uguale al carico da sollevare, il vantaggio della carrucola, è che nel
suo uso, l'operatore assume una posizione più comoda.
Un altro aspetto già visto,
è la possibilità di dimensionare il cavo sollecitato a trazione previsto
nel suo utilizzo.
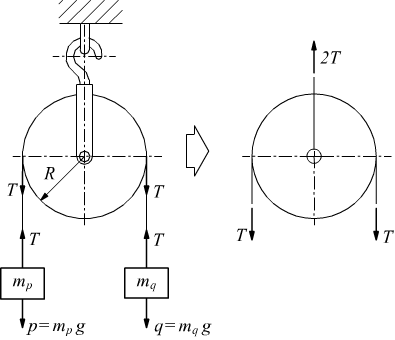 Premesso
che in condizioni di equilibrio, quando ad una carrucola sono appese
due masse uguali mp=mq , la situazione delle forze
è quella disegnata qui a fianco, dalla quale si deduce T=p=mp·g=q=mq·g
con
Premesso
che in condizioni di equilibrio, quando ad una carrucola sono appese
due masse uguali mp=mq , la situazione delle forze
è quella disegnata qui a fianco, dalla quale si deduce T=p=mp·g=q=mq·g
con
g=9,81 m/s2 :accelerazione di gravità e T: tensione (sforzo)
interno della fune [N].
Chiaramente la tensione T dipende sia da mp che da mq
ma, se mp≠mq il suo valore, in generale, non
sarà quello, comunque, nella carrucola fissa,
si deve evidenziare che la tensione della
fune T è la stessa nei due rami a cui vengono applicate le due forze
esterne.
Una variante della carrucola fissa è la carrucola
mobile, anch'essa già
vista.
La carrucola mobile è assimilabile ad una leva di secondo genere (con
fulcro in A) con il braccio della forza motrice (con punto di applicazione
B) , doppio rispetto a quello della forza resistente (con punto di applicazione
O). Dal disegno si vede la forza motrice p che agisce con braccio AB=2R
mentre la forza resistente lavora con braccio AO=R
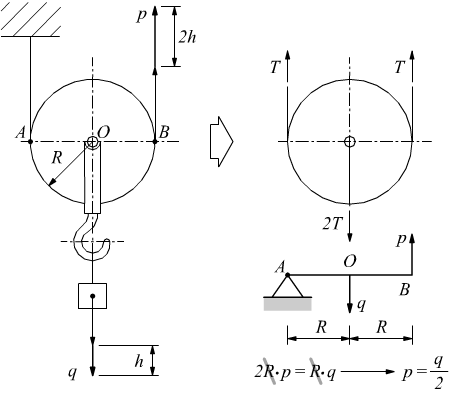
Nella carrucola mobile è dunque presente un vantaggio: se p è la forza applicata e q è il carico da sollevare si ha p=q/2. Questo si riflette sugli spostamenti effettuati dai punti di applicazione delle due forze: il lavoro effettuato dalla forza p deve essere uguale al lavoro associato alla forza q:
![]()
ma dato che p è la metà di q , deve essere
![]()
come già detto, quello che si risparmia in forza lo si spende in spostamento.
Questo ha delle implicazioni che vanno tenute conto quando si fanno
gli esercizi
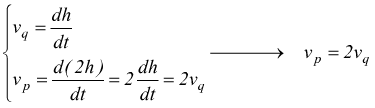
La velocità del punto di applicazione della forza motrice p è doppia rispetto alla velocità del punto di applicazione della forza resistente q. Ma sopratutto:
![]()
questa regola vale anche per le accelerazioni.
Gli esercizi che abbiamo risolto su questo argomento hanno tutti lo stesso
tipo di approccio piuttosto tradizionale, consideriamo il classico esempio
della macchina di Atwood qui sotto disegnata, dove è presente una carrucola
a cui sono appese le due masse m1 ed m2 con tutte
le caratteristiche delle condizioni ideali, cioè, assenza di attrito tra
cavo e carrucola e cavo inestensibile.
E' ragionevole pensare ed ipotizzare che se m1<m2
la massa m2 più pesante tenderà a scendere, mentre la massa m1
tenderà a salire. Esisterà dunque una causa del moto che indichiamo (in
rosso) che è l'accelerazione.
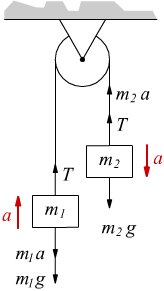
ciascuna massa sarà dotata della
sua propria forza peso (m·g) e della reazione vincolare T (tiro)
del cavo di collegamento con la carrucola.
L'accelerazione sarà evidentemente identica per entrambe le masse così
come il tiro T del cavo.
Una volta indicata l'accelerazione per ciascuna massa, indicheremo per
questa il vettore forza di inerzia (m·a) che dovrà avere verso
opposto all'accelerazione ipotizzata per quella massa, deve , ovviamente,
essere rispettata la seconda e la terza legge della dinamica
![]()
cioè la somma algebrica delle forze attive e reattive deve bilanciare la forza di inerzia.
Non dimentichiamo che la forza di inerzia si oppone alla causa del moto che è l'accelerazione, per questo motivo il vettore m·a viene rappresentato opposto all'accelerazione ipotizzata.
Nel nostro caso, le forze attive sono i pesi m·g le forze reattive, sono invece le reazioni vincolari; in questo caso il tiro T del cavo. In questo modo per le due masse si viene a creare un sistema di due equazioni dove le variabili comuni sono il tiro T e l'accelerazione.
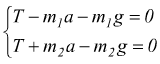
si può procedere per sostituzione oppure sottrarre membro a membro eliminando T
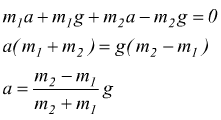
ovviamente poi possiamo trovare T ad es. con la prima equazione
![]()
se l'accelerazione trovata è negativa, non bisogna preoccuparsi, vuol dire
che il modulo dell'accelerazione è quello che abbiamo trovato, ma il verso
del vettore è contrario a quello che avevamo inizialmente ipotizzato. Basterà
rifare l'esercizio ipotizzando un vettore accelerazione contrario a quello
che avevamo scelto la prima volta per trovare conferma a questo fatto (gli
esercizi 1 e 2 dimostrano questa eventualità).
 edutecnica
edutecnica