Radicali
I radicali sono numeri ottenuti attraverso l’operazione di estrazione
di radice, la loro importanza risiede nel fatto che attraverso questa operazione
viene introdotta una nuova classe di numeri: i numeri irrazionali, che va
ad ampliare le precedenti classi dei numeri interi e razionali ( o frazionari
perché ottenuti dividendo degli interi).
L’estrazione di radice è a tutti gli effetti
l’operazione opposta a quella di elevamento a potenza.
Per definizione la radice n-esima di un numero a è quel numero b che elevato alla n restituisce a.
![]() con
le seguenti denominazioni
con
le seguenti denominazioni

Semplicemente il radicando è pari alla radice elevato all'indice di radice.
Quando l'indice di radice non appare è sottinteso che esso vale 2.
![]()
Inoltre ![]() mentre
mentre
![]() è priva di significato; ad es.
è priva di significato; ad es.
![]()
L'indice di radice deve essere valutato con attenzione, infatti, se
n dispari: il radicando (a) e e la radice (b)
sono due numeri reali (a, b ∈R); se
n pari:deve essere a≥0 e b≥0 sempre con
a, b ∈R; .
Radice quadrata
La radice quadrata di un numero reale a, è quel numero reale b, positivo o nullo che elevato al quadrato dà come risultato a.
![]() con
a,b ∈R e a≥0 e b≥0. Ad es.
con
a,b ∈R e a≥0 e b≥0. Ad es.
![]()
![]() perché
perché
![]() indica
l'opposto di
indica
l'opposto di ![]()
![]() non
esiste nessun numero x, che elevato al quadrato restituisca un numero negativo
(x2=-4). Questo giustifica la condizione richiesta a≥0 che costituisce
di fatto una condizione di esistenza del radicale.
non
esiste nessun numero x, che elevato al quadrato restituisca un numero negativo
(x2=-4). Questo giustifica la condizione richiesta a≥0 che costituisce
di fatto una condizione di esistenza del radicale.
Per le frazioni si ha 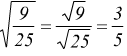 poi
ed in particolare è
poi
ed in particolare è ![]()
Modulo o Valore assoluto
Nella definizione di radicale si deve evidenziare anche la condizione b≥0. Infatti, ipotizziamo b=-3
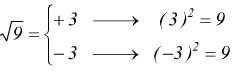
qual è l'uguaglianza corretta? Perché evidentemente 3≠-3.
Il radicale ![]() non
pone problemi per a≥0.
non
pone problemi per a≥0.
Nel caso in cui a<0 la stessa scrittura comporta una discordanza di segni
tra il primo ed il secondo membro dell'uguaglianza.
In questo caso si ricorre alla definizione di valore assoluto
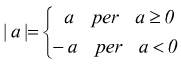
si scriverà dunque ![]() (per
ogni valore di a appartenente al campo reale). Ad esempio
(per
ogni valore di a appartenente al campo reale). Ad esempio
|5|=5
|-6|=-(-6)=6
Quindi il risultato dell'estrazione di radice risulterà sempre positivo
in accordo alla condizione della definizione b≥0.
Radice cubica
E' definita come radice cubica di un numero reale a, e si indica ![]() il
numero reale b che elevato al cubo, dà come risultato a.
il
numero reale b che elevato al cubo, dà come risultato a.
![]()
Quando l'indice di radice n è dispari, le condizioni richieste al radicando e al radicale sono meno restrittive ed è sufficiente che essi siano numeri reali (a,b ∈R).
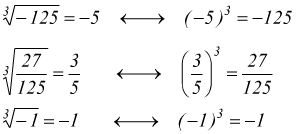
Proprietà invariantiva dei radicali
Moltiplicando l'indice di un radicale e l'esponente del suo radicando per uno stesso numero naturale diverso da zero, si ottiene un radicale equivalente a quello originario
![]()
questo per a≥0. Perché per a<0 questà proprietà può essere
falsa. Ad es. ![]() infatti:
infatti:
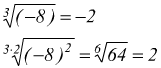
Riduzione di radicali allo stesso indice
La prima conseguenza della proprietà invariantiva dei radicali è la possibilità di ridurre più radicali allo stesso indice.
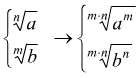 Ad es.
Ad es. ![]()
Il minimo comune multiplo tra i due indici è mcm(12;18)=36 (il 12 nel 36 ci sta 3 volte mentre il 18 nel 36 ci sta 2 volte)
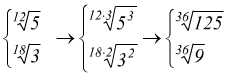
Prodotto di radicali
![]() n∈N
con n≠0
n∈N
con n≠0
Quoziente di radicali
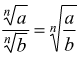 n∈N
con n≠0 e b≠0
n∈N
con n≠0 e b≠0
Elevamento a potenza di radicali
 con
n,m∈N n≠0 e m≠0
con
n,m∈N n≠0 e m≠0
Estrazione di radice di radicali
![]() con
n,m∈N n≠0 e m≠0
con
n,m∈N n≠0 e m≠0
Trasporto sotto il segno di radice
![]() con
a≥0. Se a<0 bisogna fare molta attenzione;ad es.
con
a≥0. Se a<0 bisogna fare molta attenzione;ad es.
![]()
ok ma il primo termine è negativo mentre l'ultimo è positivo, per risolvere correttamente dovevamo portare soltanto il 2 sotto il segno di radice
![]()
Trasporto fuori dal segno di radice
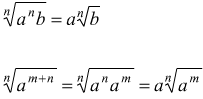
ad.es.
![]()
![]()
Addizione e sottrazione di radicali
In questo caso non valgono più le regole dell'addizione e sottrazione ordinarie, cioè
![]() infatti
infatti
![]() perché
perché
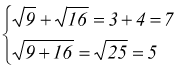 poi
poi
![]() infatti
infatti
![]() perché
perché 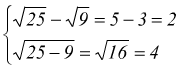
Tuttavia è sempre possibile semplificare le espressioni che si presentano utilizzando le proprietà dei radicali, riducendo a termini simili ed eseguendo raccoglimenti a fattor comune. Un raccoglimento è ad.es.
![]()
Oppure attraverso alla riduzione di radicali simili
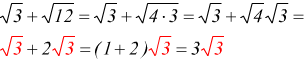
Razionalizzazione
Nelle espressioni algebriche può capitare di avere un radicale al denominatore di una frazione come
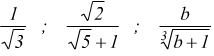
Per effettuare i calcoli, è spesso necessario che tutti i radicali siano al numeratore e questo è possibile da fare grazie all'artificio della razionalizzazione.
1° caso: ![]() si
esegue
si
esegue 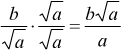 ad
es.
ad
es.
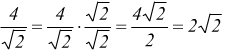
2° caso ![]() si
esegue
si
esegue 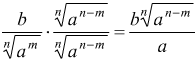 ad
es.
ad
es.
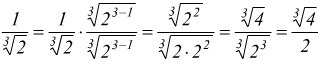
3° caso 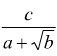 si
esegue
si
esegue 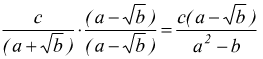 oppure
oppure
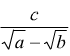 si
esegue
si
esegue 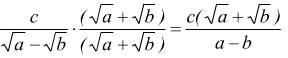
Qui si mette in evidenza l'uso della proprietà dei prodotti notevoli (A-B)(A+B)=A2-B2 , ad es.
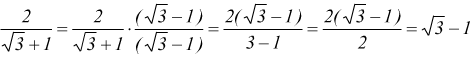
Radicali e potenze ad esponente razionale
Come già visto in precedenza il legame tra radicali e potenze ad esponente razionale è molto stretto in virtù delle regole
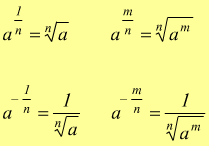
Si possono risolvere espressioni coi radicali anche attraverso le proprietà delle potenze

Numeri irrazionali ed immaginari
L'operazione aritmetica di estrazione di radice, permette di introdurre una speciale classe di numeri che è quella dei numeri irrazionali. Bisogna premettere però, che ogni classe di numeri ha le sue caratteristiche. La classe dei numeri naturali
![]()
Le regole che presiedono i numeri naturali sono molto facili ed intuitive:
• Esiste un primo numero naturale : 1.
• Ogni numero naturale è precursore (precedente) di un altro numero
naturale successivo.
• Nessun numero naturale è il successivo di se stesso.
• Nessun numero naturale ha più di un successore.
• Nessun numero naturale è il successore di più di un numero naturale.
• Soltanto il numero 1 non ha precursori.
Nell'insieme N dei numeri naturali, è sempre possibile eseguire l'adddizione e la moltiplicazione (operazioni interne ad N) mentre per poter fare delle sottrazioni o delle divisioni bisogna ampliare l'insieme N all'insieme Z degli interi relativi
![]()
E' già possibile associare all'insieme Z una sua rappresentazione geometrica: una retta sulla quale possono essere posti, equidistanti, gli elementi di Z.
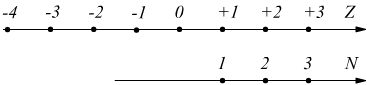
Essendo contenuto in Z, N è un sottoinsieme di Z.
Come si sa esiste una ulteriore classe di numeri: i numeri razionali (o
frazionari) .
Questo insieme viene indicato con la lettera Q ed è costituito da tutti
i numeri relativi che possono essere scritti sotto forma di frazione, essi
rappresentano tutti i numeri relativi (con segno) che esprimono tutti i
numeri che abbiano un numero di decimali finito oppure infinito ma
periodico, ad es.
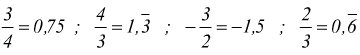
Il diagramma sottostante illustra la gerarchia tra gli insiemi
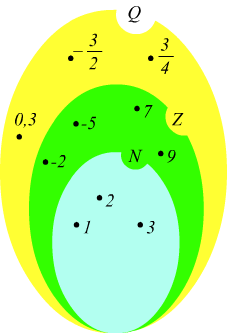
Si deve notare che i numeri razionali sono ottenuti solo da frazioni si possono
scrivere come:
•numeri decimali limitati
•numeri decimali illimitati periodici
Anche i numeri razionali possono essere posizionati sulla linea retta
vista prima che tuttavia, dovrà essere considerata ancora costituita
da punti discreti, cioè tra un punto ed un altro ci sarà sempre e comunque
dello spazio.
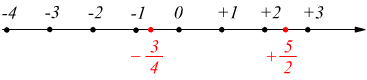
L'operazione di estrazione di radice non può essere espressa attraverso
una frazione ed introduce una ulteriore classe di numeri: la classe
dei numeri irrazionali.
Un numero irrazionale è ogni numero relativo (positivo o negativo) la cui rappresentazione decimale è illimitata e non periodica.
Esempi di numeri irrazionali sono
![]()
L'insieme formato dall'unione dei numeri razionali e dei numeri irrazionali viene chiamato insieme dei numeri reali e viene indicato con la lettera R.
La rappresentazione sul diagramma di Venn deve essere aggiornata
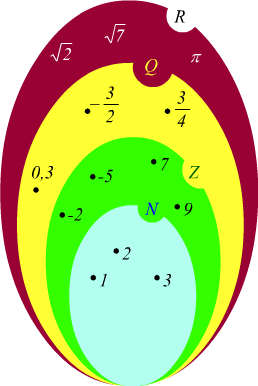
La retta, precedentemente costruita posizionando i vari numeri a secondo della loro classe di appartenenza, viene ora completata; perché l'aggiunta dei numeri irrazionali riesce a completare la sua composizione e da retta costituita da elementi (punti) discreti ora può essere considerata una vera e propria linea retta dotata di continuità.
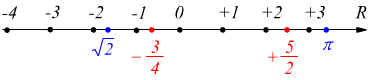
Sia l'insieme dei numeri razionali che l'insieme dei numeri irrazionali sono infiniti e densi sulla retta numerica; tra due numeri razionali si può sempre trovare un altro numero razionale e lo stesso vale per i numeri irrazionali; cioè: tra due numeri qualsiasi, sia che siano razionali o irrazionali, esistono infiniti numeri razionali ed infiniti numeri irrazionali.
Dopo aver disegnato sulla retta numerica tutti i numeri razionali ed irrazionali non esisteranno più spazi su di essa; i numeri reali, costituiti dall'unione dei numeri razionali ed irrazionali, riempiono completamente tutti gli spazi della retta senza lasciare nessun intervallo o punto vuoto.
Ad ogni numero reale corrisponde un punto sulla retta e ad ogni punto sulla retta corrisponde un numero reale.
Ovviamente, la storia della teoria dei numeri non finisce qui. Dopo aver definito questo ordine di cose alcuni problemi rimanevano irrisolti; ad esempio, cosa fare quando un numero si presenta sotto il segno di una radice con indice pari ?
![]()
La necessità di poter gestire anche queste eventualità ha portato alla definizione di una ulteriore classe di numeri: la classe dei numeri immaginari.
Un numero immaginario può essere identificato da qualsiasi numero reale con prefisso o postfisso 'i' (in elettrotecnica usiamo la 'j' per non confondersi con il simbolo della corrente elettrica). La lettera 'i' viene chiamata operatore immaginario. Si pone :
![]()
questo per definizione. Quindi, quando si presenta un caso come quello precedente
![]()
L'unione dei numeri reali e dei numeri immaginari andrà a costituire una
nuova classe di numeri: la classe dei numeri complessi indicata con la lettera
C.
Questo, però, comincia a diventare un altro
argomento.
 edutecnica
edutecnica