Numeri complessi
La radice quadrata di un numero negativo, ad es.
![]()
viene chiamato numero immaginario. Dalle proprietà dei radicali, sappiamo che
![]()
viene, quindi, introdotto l'operatore immaginario
![]() dotato
della proprietà
dotato
della proprietà
![]()
Per l'operatore immaginario, in matematica si usa il postfisso ( o anche
prefisso ) i , mentre in elettrotecnica è più frequente
trovare il prefisso j , ovviamente, perchè il simbolo i
verrebbe confuso col simbolo della corrente elettrica.
Un numero nella forma
![]()
con a e b numeri reali, viene chiamato
numero complesso con
a=parte
reale;
b=parte
immaginaria ;
I numeri complessi contengono tutti i numeri reali e tutti i numeri
immaginari perchè 7=7+0i e 4i=0+4i.
Due numeri complessi a+bi e c+di sono uguali solo se a=c e b=d.
Il coniugato di un numero complesso
a+bi è il numero complesso a-bi; cioè è lo stesso
numero dato, con la parte immaginaria invertita di segno.
Operazioni aritmetiche coi numeri complessi
Addizione : per sommare due numeri complessi si
fa la somma delle parti reali e delle parti immaginarie.
Ad es.
![]()
![]()
Sottrazione : per sottrarre due numeri complessi si fa la differenza delle parti reali e delle parti immaginarie.Ad es.
![]()
![]()
Moltiplicazione : per moltiplicare due numeri complessi si effettua il prodotto come se i due numeri fossero dei semplici binomi, sostituendo poi i2 con -1.
![]()
![]()
![]()
![]()
Divisione : per dividere due numeri complessi si moltiplicano numeratore e denominatore della frazione per il coniugato del denominatore.


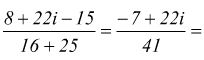

A
B
Rappresentazione grafica di numeri complessi
Il numero complesso a+bi può essere rappresentato da un punto P con
coordinate ( a,b ). Il punto O che ha coordinate ( 0, 0 ) e che rappresenta
il numero complesso 0+0i=0.
Tutti i punti dell'asse orizzontale, delle ascisse, rappresentano i numeri
reali.
Tutti i punti dell'asse verticale, delle ordinate, rappresentano i numeri
immaginari.
Per questa ragione l'asse orizzontale viene chiamato asse
reale.
L'asse verticale viene chiamato asse immaginario.
Il piano cartesiano che ha queste caratteristiche viene chiamato piano
complesso o piano di Gauss.


Sul piano complesso, oltre che dal punto P, un numero complesso può essere rappresentato dal vettore OP.


Trattandosi di vettori, per i numeri complessi l'operazione di somma e
differenza può essere eseguita anche graficamente, tramite la regola
del parallelogramma o attraverso il metodo punta-coda, già visto
nel caso dei vettori.
Una resa grafica delle quattro operazioni aritmetiche sui numeri complessi
è disponibile per chi ha
( ancora ) un browser java-enabled in
questa pagina.
Forma polare di numeri complessi
Oltre alla forma algebrica o binomiale appena vista, i numeri complessi
possono essere rappresentati attraverso la forma polare.
In pratica, invece di usare le due coordinate cartesiane a e b,
si usano le due coordinate polari ρ e θ. ρ=modulo
o intensità del vettore; cioè ( graficamente ) la sua lunghezza.
θ=argomento
( o fase ) cioè l'angolo che il vettore forma con l'asse reale.

![]() modulo
modulo
 argomento
argomento
a:parte reale
b:parte immaginaria
Dopo aver specificato che gli argomenti sono positivi se si svolgono in senso antiorario rispetto l'asse reale, dalla trigonometria si ha:
![]()
La forma polare di un numero complesso è dunque $ρe^{jθ}$ con
e=numero di Neper=2,2718.. in pratica la relazione fra forma polare
e forma binomiale è
![]()
se ρ=1 e θ=π la precedente formula diventa
$e^{jπ}+1=0$ nota come la formula di Eulero.
L'importanza della formula di Eulero sta nel fatto che essa stabilisce, tramite i numeri complessi, la stretta relazione che esiste tra la funzione esponenziale e le funzioni trigonometriche.
modulo
argomento
La forma polare è particolarmente vantaggiosa quando si devono eseguire moltiplicazioni e divisioni fra numeri complessi.

 edutecnica
edutecnica