Potenze
Dopo le quattro operazioni fondamentali dell’aritmetica (+, -, ×, /) l’elevamento a potenza di un numero, con le sue proprietà può essere ritenuta l'operazione successiva più importante; essa è in grado di facilitare o abbreviare calcoli molto complicati con numeri estremamente grandi o piccoli.
Così come la moltiplicazione può essere considerata una addizione ripetuta
3+3+3+3=3×4=12
L'elevamento a potenza non è altro che una moltiplicazione ripetuta
3×3×3×3=34=81
Il simbolo 34 rappresenta l'operazione di elevamento a potenza.
L'elevamento a potenza, è dunque, un'operazione che consiste nell'accostare una coppia di numeri: la base e l'esponente che rappresentano il numero che si ottiene moltiplicando tanti fattori uguali alla base quanti ne indica l'esponente.
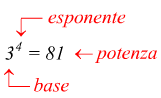
In questo caso :
3 è la base cioè il numero che deve essere moltiplicato per se stesso.
4 è l'esponente cioè il numero che indica quante volte la base 3 deve essere
moltiplicata per se stessa.
La scrittura 34 si legge 'tre alla quarta' o 'tre elevato alla
quarta potenza'.
81=3· 3· 3·3=34 è il risultato dell'operazione
di elevamento a potenza.
Proprietà delle potenze
Le seguenti proprietà valgono per esponente n≠0 (e anche m≠0) inoltre la base a può essere un qualsiasi numero reale (con la virgola) a∈R.
Il prodotto di due o più potenze di ugual base è una potenza con la stessa base che ha per esponente la somma degli esponenti
Infatti se consideriamo l'operazione 34·33 avremo (3·3·3·3) · (3·3·3)=37=34+3 ad esempio :
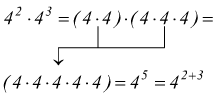
Il quoziente di due potenze di ugual base è una potenza della stessa base che ha per esponente la differenza degli esponenti:
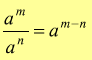ad
esempio
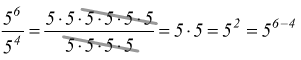
Questo è quanto accade quando m>n ma se l'esponente del numeratore è minore di quello al numeratore cosa accade?
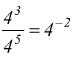ma
che numero rappresenta 4-2 ? 
che
porta a definire la proprietà :
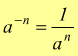
Una potenza che ha una base con esponente negativo è uguale al reciproco
di quella base con lo stesso esponente preso come positivo.
Nel caso in cui risulti m=n si avrebbe:
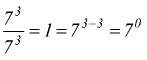che porta a definire la proprietà
ogni
numero elevato all'esponente 0 è uguale a 1.
Dalle considerazioni precedenti si deduce anche la proprietà
ogni numero elevato all'esponente 1 è uguale a se stesso.
Questa proprietà delle potenze si può dedurre come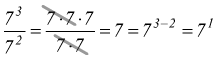 
Non dovrebbe poi essere difficile constatare che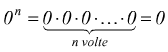 
.
Il numero 0, elevato a qualsiasi esponente maggiore di 0, è uguale a 0.
La potenza 00 è considerata priva di significato.
Un'altra proprietà notevole è la seguente
La potenza di una potenza è una potenza che ha per base la stessa base e per esponente il prodotto degli esponenti.
Se ci pensiamo l'operazione sarebbe la seguente
Inoltre si ha:
Il prodotto di due o più potenze di uguale esponente è una potenza con lo stesso esponente che ha per base il prodotto delle basi. Come si constata
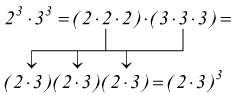allo
stesso modo si può dire
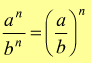
Il quoziente di due potenze di uguale esponente è una potenza con lo stesso esponente che ha per base il quoziente delle basi.
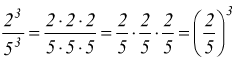
Potenze ad esponente razionale
Potenza ad esponente razionale, significa esponente frazionario, quindi
prendiamo la potenza 
alla
quale non sappiamo ancora attribuire un significato; applichiamo ad essa
la proprietà della potenza di una potenza
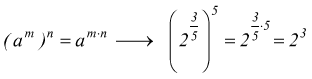per
la definizione di radicale che è
sarà 
allora, è possibile estrapolare la seguente regola
In particolare avremo
Per applicare questa regola deve essere a≥0 con n ed m numeri naturali (interi) con n≠0. La frazione all'esponente può anche essere negativa
In questo caso deve essere strettamente a>0 e sempre, con n,m ∈ N (appartenenti all'insieme dei numeri naturali) si conclude
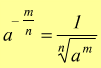
ovviamente, anche in questa circostanza, si ha il caso particolare
