Segnali

Con la parola segnale si intende una funzione del tempo che rappresenta, appunto, l'andamento temporale di una determinata grandezza fisica, come la massa di un corpo, la pressione atmosferica, la temperatura, la velocità di un’auto ecc.

Queste grandezze vengono trasformate, tramite opportuni sensori o trasduttori, in un segnale elettrico (tensione o corrente), trasferendo su questa grandezza fisica, peculiarità e caratteristiche del segnale originario.
A quel punto è possibile coniugare il concetto di segnale anche al tipo di informazione che esso può contenere e si può affermare che il segnale rappresenta il "supporto fisico" su cui viaggia l'informazione. Ricorriamo al segnale per trasmettere informazioni, elaborarle, manipolarle.
Il legame tra grandezza fisica e segnale è molto importante; l’elettronica si è sviluppata nel corso del tempo con l’obiettivo di studiare questo tipo di segnali e degli apparati idonei alla loro manipolazione.
Un esempio piuttosto tradizionale è la costituzione di un impianto Hi-Fi per la riproduzione di dischi musicali degli anni ’70.

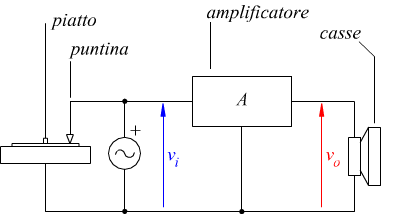
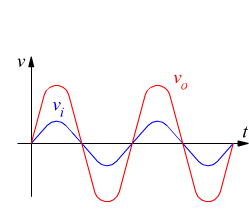
Nello schema è possibile riconoscere il piatto su cui viene messo il disco. Il disco messo in rotazione, entra in contatto con una puntina che produce vibrazioni meccaniche, queste vibrazioni vengono trasformate in un segnale elettrico che poi viene opportunamente amplificato dall'amplificatore, mantenendo invariata la sua frequenza. Il segnale amplificato, viene poi inviato ai finali di potenza, cioè, alle casse che, facendo vibrare le membrane, riproducono il suono amplificato.
In questo schema il dispositivo piatto-puntina costituisce il trasduttore, perche trasforma il segnale fisico (la vibrazione meccanica) in segnale elettrico. Mentre le casse costituiscono l'attuatore, che esegue l'operazione inversa, trasformando il segnale elettrico in suono, cioè, in una grandezza fisica.

Per trasmettere informazioni in un sistema di comunicazione o di misura, si usa dunque, come mezzo di trasporto, una grandezza elettrica variabile nel tempo, denominata segnale, sulla quale viene caricata l'informazione.

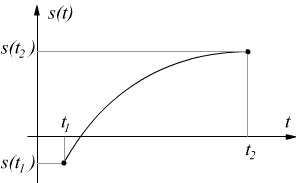
Un segnale è detto analogico o continuo, se la forma d'onda che lo rappresenta è una funzione continua nel tempo, cioè se essa, può assumere con continuità gli infiniti valori compresi tra due estremi.

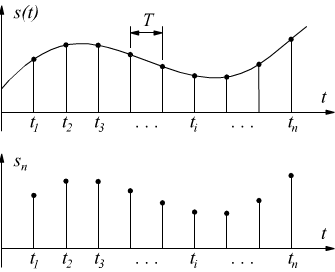
Un segnale discreto, è per definizione un segnale che viene rilevato in corrispondenza di determinati istanti definiti, la cui distanza temporale può essere qualsiasi. Nel settore elettronico i segnali discreti di maggior interesse sono quelli in cui gli istanti del rilevamento sono equidistanti di un intervallo di tempo T (periodo).
Questa operazione di rilevazione periodica viene anche chiamata campionamento.
(ma non solo, ad es. nel settore dei giochi a premi, l'estrazione del superenalotto avviene sempre di sabato, quindi, la rilevazione dei numeri è temporizzata su un periodo T di una settimana) .

Un segnale viene detto quantizzato quando tra due suoi valori successivi non possono esserci altri valori.
Ad esempio l'insieme dei numeri naturali relativi è quantizzato (con quanto Q=1) perche tra 2 e 3 non può esserci nessun altro valore, cosi come tra -7 e -6.

Un segnale digitale è un segnale simultaneamente discreto e quantizzato, è dunque un segnale che può variare solo in determinati istanti di tempo assumendo esclusivamente determinati valori, pari al quanto o a un multiplo del quanto.

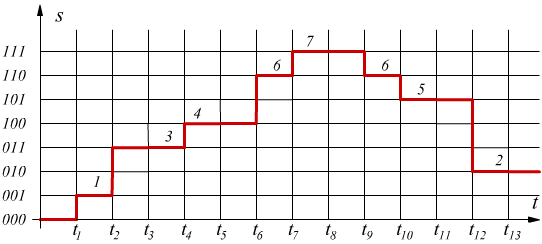
Sarebbe tecnicamente possibile realizzare un segnale quantizzato ma non discreto oppure discreto ma non quantizzato, ma queste tipologie di segnale non possono essere annoverate come digitali.

Il campionamento e la quantizzazione formano un'unica operazione detta codifica.
Per eseguire la codifica vengono usati dei convertitori analogico-digitali (ADC).
Una volta effettuata questa operazione il segnale è convertito in forma numerica e può essere reso disponibile ad un elaboratore elettronico digitale (calcolatore).

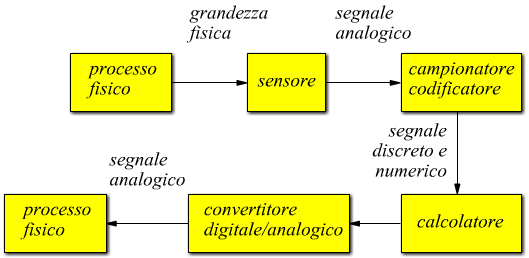
L'operazione inversa a quella descritta consiste nella trasformazione del segnale digitale in segnale analogico al fine di restituire un processo a tempo continuo. Il componente elettronico che permette di effettuare questa operazione è il convertitore digitale-analogico (DAC).

I segnali di comunicazione digitale presentano notevoli vantaggi rispetto ai sistemi analogici. Fondamentalmente se ne possono elencare tre:

● Miglioramento del rapporto segnale/rumore (S/N) .
● Possibilità di essere elaborati da microprocessori .
● Possibilità di impiego dei segnali digitali nel campo della trasmissione dei dati, della telefonia e della TV ad alta qualità.

Teorema del campionamento

Per effettuare un buon campionamento è necessario prelevare da ogni segnale delle porzioni aventi durata molto piccola in intervalli regolari T_c.

Il campionamento si deve effettuare rispettando alcune regole per non perdere l'informazione; in altri termini, il segnale analogico deve essere campionato in modo da rendere possibile in ricezione la propria ricostruzione. Questa regola regola è stabilita dal teorema di Shannon chiamato anche teorema del campionamento.

La frequenza con la quale si deve campionare un qualsiasi segnale deve essere maggiore di due volte la frequenza massima dello stesso segnale:

l'intervallo di campionamento vale .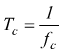

La relazione di Shannon può anche essere espressa come f_c≥2B se il segnale da campionare occupa una banda di frequenza B=0÷f_c.
Il teorema di Shannon stabilisce un limite minimo , in pratica la frequenza di campionamento può raggiungere 3÷4 volte la frequenza massima del segnale analogico da convertire.

L'operazione di campionamento ideale può essere pensata come un interruttore al quale viene applicato il segnale da campionare, la cui apertura e chiusura avvengono con una frequenza pari ad f_c : quando l'interruttore resta chiuso , viene prelevata una porzione del segnale di ingresso, resta invece aperto negli altri istanti.

Poiché nel caso reale tra l'istante in cui si chiude e l'istante in cui si apre il tasto dell'interruttore passa un determinato intervallo di tempo, ciascun campione prelevato avrà una certa durata τ. Il segnale analogico campionato S(t_n) in questo caso può essere rappresentato come un segnale tagliato a fette dalle quali si prelevano alcune di esse in intervalli di tempo prestabiliti.

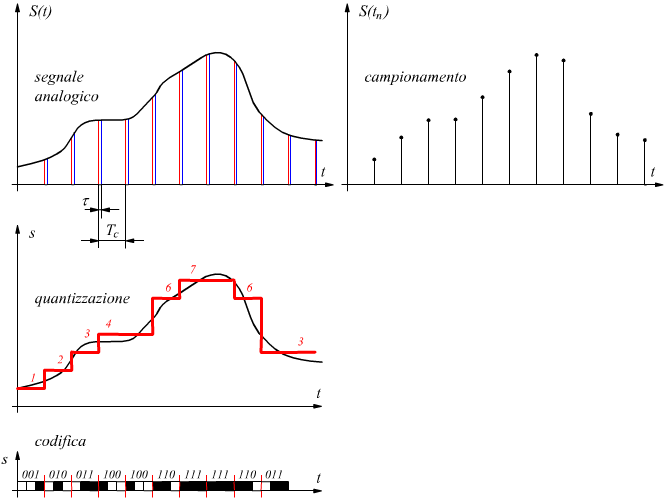
In pratica il campionamento si effettua in modo periodico negli istanti

T_c = periodo di campionamento; n=1, 2, 3,..

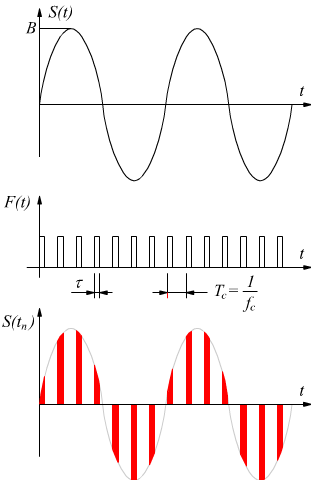
Un segnale campionato, può essere pensato come il prodotto tra il segnale analogico S(t) da acquisire ed un segnale formato da un treno di impulsi F(t) ideali (δ di Dirac) o di durata τ→0 infinitesima avente frequenza f_c pari a quella stabilita dal teorema di Shannon chiamata anche funzione campionatrice.

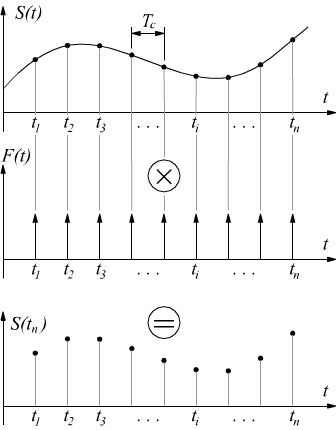
Spettro di un segnale campionato

Per studiare cosa accade ad un segnale che viene campionato ad una frequenza f_c costante possiamo accennare due approcci, entrambi effettuati su una forma d'onda di tipo sinusoidale.

Campionamento istantaneo

Nel caso ideale la funzione campionatrice F(t) è considerata come un treno di impulsi con frequenza di ripetizione pari alla frequenza di campionamento ma di durata τ infinitesima, cioè viene intesa come un treno di impulsi di Dirac o δ.

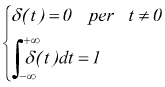
Si può, quindi, pensare l'impulso δ come un impulso ad onda quadra di area unitaria ( di ampiezza 1/τ e larghezza τ) per τ→0.

quindi nel caso della funzione campionatrice sarà

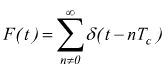sviluppando in serie di Fourier si ha

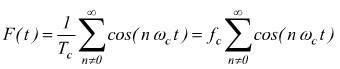
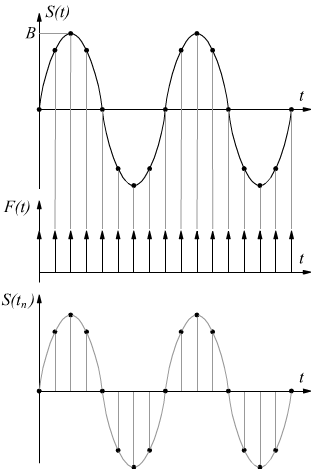
Se l'onda S(t) da campionare per semplicità si suppone sinusoidale di ampiezza B e frequenza f_m (frequenza massima) allora in segnale campionato avrà espressione :

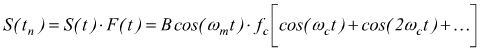
quindi

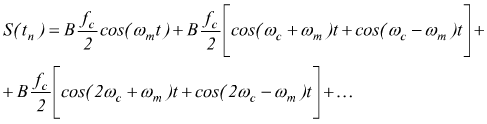
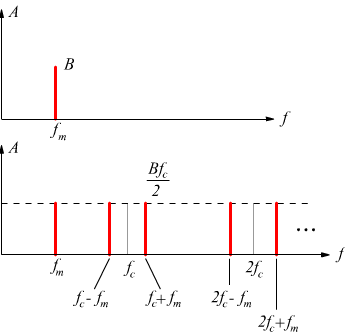
Si deduce che lo spettro di frequenza è composto da 2n+1 termini in cui

● il primo termine è l'informazione del segnale originario;
● i restanti termini rappresentano le componenti centrate attorno alla frequenza di campionamento f_c e alle sue armoniche, ossia f_c , 2f_c , 3f_c ecc..

Notiamo che tutte le componenti di frequenza che appartengono allo spettro hanno tutte la stessa ampiezza .

Campionamento naturale

In questo caso il treno di impulsi della frequenza campionatrice F(t) è costituito da onde rettangolari di durata τ e quindi di durata non infinitesima. E' possibile sviluppare tale segnale in serie di Fourier come:

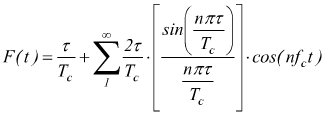
oppure indifferentemente come

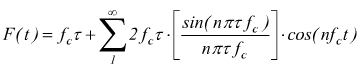
se vogliamo semplificare, si può scrivere

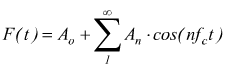
con se poniamo x=nπτf_c sarebbe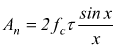

Se il segnale S(t) da campionare è sinusoidale di ampiezza B e frequenza f_m , il segnale campionato S(t_n) si può esprimere attraverso il prodotto tra F(t) e S(t).

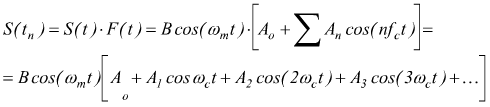
ricordando le formule di Werner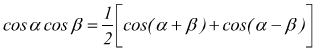

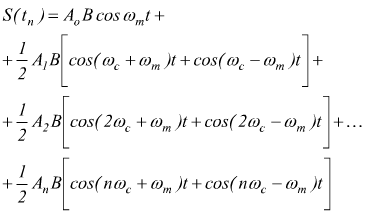
quest'ultima espressione è composta da 2n+1 termini

● il primo termine è l'informazione del segnale originario;
● gli altri termini contengono le componenti di ordine superiore centrate attorno alle frequenze f_c , 2f_c , 3f_c ecc..

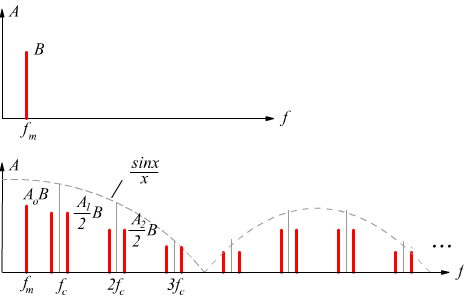
Notiamo come le righe della risposta in frequenza non abbiano un'ampiezza costante come nel caso del campionamento istantaneo, inoltre, le stesse ampiezze variano in ragione dell'inviluppo di in valore assoluto; questo perchè, ovviamente, non esistono ampiezze negative.

Ricostruzione del segnale campionato

La ricostruzione del segnale campionato, può sortire differenti effetti, a secondo delle seguenti eventualità

1 f_c > 2f_m
2 f_c = 2f_m
3 f_c < 2f_m

Nel caso 1 (f_c > 2f_m) lo spettro del segnale campionato è il seguente

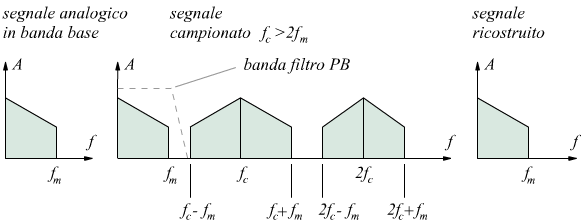
Vediamo come le bande laterali, centrate attorno alle frequenze f_c , 2f_c , 3f_c ecc.. sono distanziate tra loro da una interbanda vuota crescente, al crescere di f_c.
Lo spettro del segnale campionato contiene il segnale utile e per la ricostruzione dell'informazione occorre solo eliminare tutte le componenti di frequenza prodotte dal processo di campionamento tranne quelle appartenenti alla banda del segnale utile.
Questo, può essere agevolmente ottenuto con un filtro passa basso con una frequenza di taglio f_m < f_t < f_c-f_m .
Le interbande vuote, permettono, dunque, di separare facilmente il segnale utile dalle altre frequenze presenti nello spettro, questo grazie al fatto che il campionamento è stato effettuato rispettando il teorema di Shannon.

Nel caso 2 (f_c=2f_m) il teorema di Shannon viene formalmente rispettato e quindi questa eventualità è teoricamente accettabile. In pratica, però, la condizione limite risulta essere problematica per la corretta ricostruzione del segnale, come risulta anche dal seguente disegno:

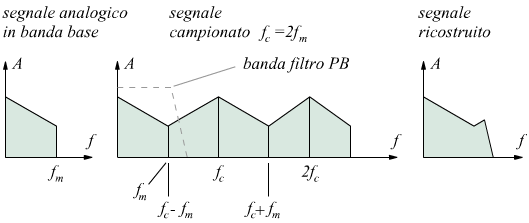
Si vede come per separare la banda del segnale utile dalle altre frequenze indesiderate bisognerebbe utilizzare un filtro ideale con pendenza verticale.
Infatti la frequenza massima della banda base del segnale utile e quella minima corrispondente alla banda inferiore, rispetto alla frequenza di campionamento f_c coincidono (intervallo di guardia nullo); in pratica, le due bande in questione si toccano. In tal caso la ricostruzione corretta è possibile solo se la risposta del filtro è molto rapida, cioè in grado di separare nettamente le due bande.
E' ovvio che usando un filtro reale che abbia una risposta come quella disegnata (in tratteggio) la ricostruzione del segnale originario produce effetti di distorsione, in quanto una parte delle delle componenti di frequenza, appartenenti alla banda inferiore, viene lasciata passare col segnale utile.

Nel caso 3 (f_c < 2f_m) in cui il segnale viene campionato con frequenza o velocità di campionamento inferiore alla condizione limite definita dal teorema di Shannon, vi sarà addirittura una perdita di informazione con distorsione in acquisizione.

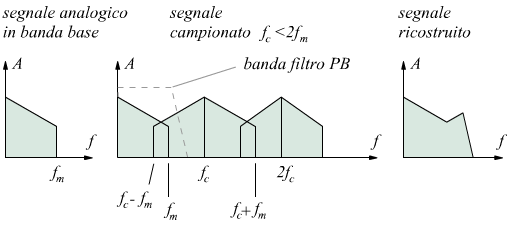
Infatti le frequenze, che normalmente capitano fuori dalla banda di frequenza del segnale originario sono traslate all'interno di tale banda sovrapponendosi ad essa ; in questo modo, dopo la consueta operazione di filtraggio, il segnale risulterà sicuramente distorto. Questo effetto viene chiamato aliasing che potrebbe essere inteso col termine "frequenze fantasma" dato che nel segnale acquisito vengono introdotte delle frequenze che nel segnale originale nemmeno esistevano.

Larghezza dell'impulso

Oltre ai fattori che abbiamo accennato, bisogna specificare che la qualità del del processo di conversione analogico-digitale viene anche influenzata dalla larghezza dell'impulso di campionamento. Osservando i termini della funzione campionatrice F(t) nel caso di campionamento naturale, avremo

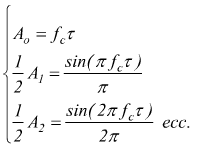
Si nota che al variare della larghezza dell'impulso τ varia solo l'ampiezza della banda laterale dello spettro del segnale campionato essendo f_c=cost.
Si osserva che esiste una relazione di proporzionalità diretta tra la larghezza degli impulsi τ della F(t) e l'ampiezza delle bande laterali A_c.
Cioè all'aumentare o diminuire dell'ampiezza dell'impulso τ aumentano o diminuiscono le ampiezze dell bande laterali dello spettro del segnale campionato e risultano sempre A₁ > A₂ , A₂ > A₃ ecc.

Si conclude che la larghezza dell'impulso della funzione campionatrice può influenzare la ricostruzione del segnale acquisito. Un esempio tipico di questa possibilità viene riscontrata, talvolta, nei sistemi telefonici in cui la frequenza di campionamento non ha mai valori elevati e capita che i filtri passa basso, usati in ricezione per la ricostruzione del segnale campionato non siano in grado di attenuare fortemente le frequenze sopra i 3,4 kHz prelevando anche se in modo attenuato, una componente della banda laterale inferiore, come si nota nel seguente disegno:

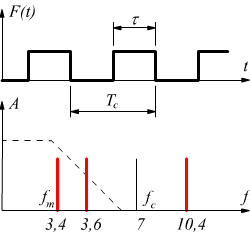
Questo puo avvenire fissando la frequenza di campionamento già a 7 kHz . Si ottiene, infatti, una riga spettrale corrispondente alla banda laterale inferiore collocata a 7-3,4=3,6 kHz. Se la larghezza degli impulsi della funzione campionatrice è grande, il filtro non riesce ad attenuare fortemente l'ampiezza della banda laterale a 3,6 kHz ed il segnale ricostruito verrà distorto.

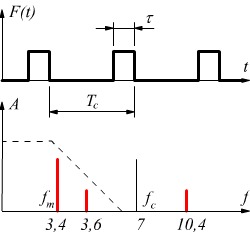
Si può, in questo caso, rimediare riducendo la larghezza degli impulsi riducendo l'ampiezza di questa banda laterale; in questo modo, anche se il filtro non attenua fortemente questa componente, il suo effetto sul segnale ricostruito sarà trascurabile.