Passaggio al limite
Studiando le coniche (retta, parabola, iperbole etc..) abbiamo visto come
queste funzioni matematiche abbiano anche un significato geometrico e possano
essere rappresentate graficamente su un piano cartesiano costituito da una
coppia cartesiana di assi coordinati (x, y).
Per studiare una generica funzione potremmo usare un metodo pratico, come
quello di calcolare il valore della y per valori progressivi della x e poi
di riportare le coppie di coordinate ottenute sul piano cartesiano congiungendole
con una spezzata poligonale che dovrebbe costituire un grafico approssimato
della nostra funzione.
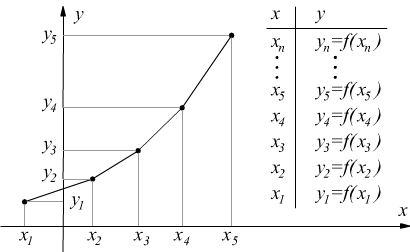
Ma questo metodo oltre ad essere laborioso, si rivela alla lunga insoddisfacente perchè per quanto piccolo possa essere scelto l’intervallo tra due valori della x, esiste sempre la possibilità che in quell’intervallo la funzione abbia un comportamento inaspettato che noi mancheremmo di rilevare.

Occorre dunque cambiare approccio allo studio del comportamento di una funzione, in modo particolare in prossimità dei punti del suo dominio di esistenza in cui essa risulta essere indefinita. Il passaggio al limite è un'operazione matematica che ci permette di analizzare il comportamento di una funzione nell'intorno di un opportuno punto o nell'intorno di infinito (∞).
Intorno
Si chiama intorno di un punto xo un qualunque intervallo aperto che contenga il punto xo .
Si possono avere le seguenti eventualità
intorno di xo
![]()
intorno circolare di xo di raggio
δ

intorno destro di xo

intorno sinistro di xo

Si chiama intorno di +∞ un qualunque
intervallo aperto del tipo $(a,\, +∞)$;
![]()
in modo analogo, si chiama intorno di $-∞$
un qualunque intervallo aperto del tipo $(-∞,\, b)$
![]()
per studiare i limiti è importante anche tener conto della definizione di punto di accumulazione. La definizione di punto di accumulazione è la seguente:
Un punto P, appartenente o no all'insieme A, si dice punto di accumulazione per A, se in ogni suo intorno esistono elementi di A.
Da cui deriva la definizione di punto isolato.
Un punto di A, che non sia punto di accumulazione per A si dice punto isolato.
Fatte queste premesse vediamo come si può introdurre intuitivamente la nozione di limite.
● esempio : prendiamo la funzione
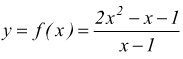
che ha come dominio di esistenza D≡R-{1}; (cioè x ≠ 1)cerchiamo di capire il comportamento della funzione quando si scelgono valori di x prossimi (molti vicini) ad 1 che poi è il punto in cui la funzione risulta indefinita.
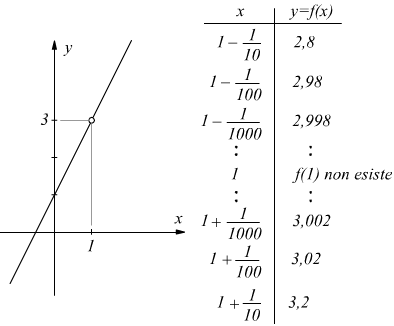
dalla tabella del grafico si intuisce che se x tende ad 1 per difetto (da sinistra) i valori della funzione tendono a 3 (per difetto) mentre se x tende ad 1 per eccesso (da destra i valori della funzione tendono a 3 per eccesso. In simboli si scrive:
![]()
e si dice che il "limite per x che tende ad 1 di f(x) è 3" le approssimazioni per difetto e per eccesso si possono invece scrivere come
![]()
Facciamo notare che nel punto x=1 la funzione non esiste (perchè si ha una divisione per 0) come viene confermato dalla computazione della precedente funzione eseguita con l'excel
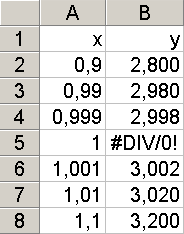
Accertato il fatto che più x si avvicina ad 1 tanto più f(x) si avvicina a 3, scopriremo che se prendiamo un qualunque valore di x in un intorno di 1 sempre più piccolo, allora f(x) si trova sempre più vicino a 3, cioè, cioè si trova in un intorno di 3 sempre più piccolo
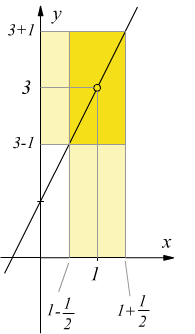
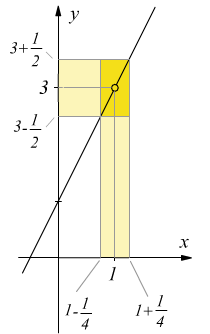
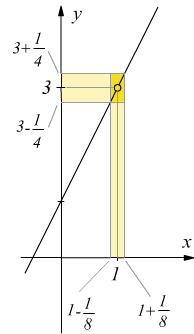
Possiamo allora dire che, se consideriamo un qualunque intorno circolare di 3 di ampiezza ε che indichiamo E di 3 allora esiste sempre un intorno di 1 i cui punti di x (con x≠1) hanno i valori di f(x) contenuti in E.
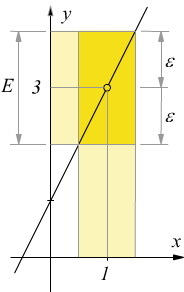
Infatti i punti che soddisfano la disequazione
 sono,
sviluppando i calcoli
sono,
sviluppando i calcoli
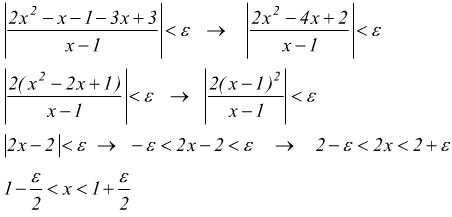
poichè la soluzione è un intorno di 1 il limite è verificato.
Definizione di limite
Possiamo ora, dare la definizione di limite di una generica funzione y=f(x) rispetto al valore xo che sia un punto di accumulazione per il dominio D della funzione anche se xo può appartenere a D oppure no.
Si dice che la funzione y=f(x), per x che tende ad
xo , ammette il limite l e si scrive
$\lim↙{x→x_o}f(x)=l$
se, comunque si scelga un numero ε>0, a questo resta coordinato
un numero δ>0 in modo tale che per ogni x dell'intorno di xo
|x-xo|<δ eccettuato al più il punto xo stesso
f(x) sia compresa nell'intervallo (l-ε,l+ε) cioè si abbia
|f(x)-l|<ε .
Simbolicamente si scrive: ![]()
La definizione precedente può essere interpretata facendo riferimento ad una generica funzione y=f(x) rappresentabile da una curva come quella sotto disegnata
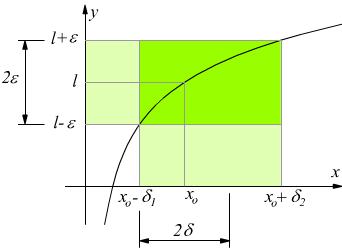
Scegliere un ε arbitrario e positivo significa fissare sull'asse
y i punti l+ε ed l-ε per i quali tracciamo le parallele
all'asse x sino ad incontrare la curva.
Se la curva viene incontrata nei punti di ascissa xo-δ1
ed xo+δ1, detto δ
il minore tra i due numeri δ1 e δ2 otteniamo
l'intorno circolare 2δ di xo.
● esempio ![]()
bisogna provare che scelto un ε>0 esiste un'intorno completo di 2 per ogni x del quale (escluso al più il 2) si ha |(3x-1)-5|<ε.
![]()
![]()
cioè:
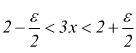 e
si riconosce che se si sceglie
e
si riconosce che se si sceglie ![]()
ogni x che soddisfa la condizione |x-2|<δ soddisfa anche la |(3x-1)-5|<ε.
● esempio 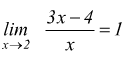
Secondo la definizione data, in corrispondenza di un ε>0 prefissato, si dovrà determinare un numero δ, tale che per ogni x (diverso da 2) soddisfacente la condizione
![]() si
abbia
si
abbia 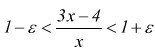
risolviamo quest'ultima rispetto ad x:

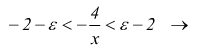
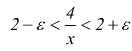 cioè
cioè
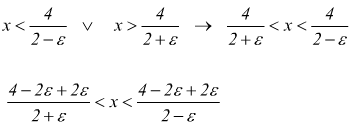
farebbe 
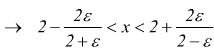
da cui si riconosce che se si sceglie δ il più piccolo dei due numeri $${2ε}/{2+ε}$$ e $${2ε}/{2-ε}$$
per ogni x che soddisfa la $2-δ<x<2+δ$ viene soddisfatta la $$1-ε<{3x-4}/x<1+ε$$
può accadere che la y=f(x) non sia definita per x>xo in tal caso deve essere |f(x)-l|<ε per ogni x≠xo ed appartenente all'intorno sinistro (xo-δ, xo) cioè sarà xo-x<δ . Si potrà dire, allora, che il numero l è il limite sinistro della funzione per x tendente ad xo e si scrive
![]()
Se, invece, la funzione non è definita per x<xo , sarà |f(x)-l|<ε per ogni x≠xo e appartenente ad un intorno destro (xo, xo+δ) di x, e in tal caso il limite l della funzione viene chiamato limite destro, per x tendente ad xo dalla destra e si scrive
![]()
● esempio

La funzione sotto il segno di radicale, ha dominio $$x≥2/3$$ ; non ha senso, dunque, indagare su punti che stanno a sinistra di $$x=2/3$$. Scelto un numero ε positivo arbitrario, si dovrà determinare un intorno destro di $$2/3$$, tale che per ogni x soddisfacente alla condizione
a 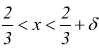 si
abbia
si
abbia ![]() b
b
essendo $√{3x-2}$ un radicale aritmetico la disuguaglianza a sinistra è sempre verificata; l'altra
![]() è
verificata per
è
verificata per 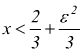
se scegliamo ![]() ogni x che soddisfa la a soddisfa
anche la b .
ogni x che soddisfa la a soddisfa
anche la b .
Limite infinito per x che tende a un valore finito
Si dice che la funzione y=f(x), per x che tende ad
xo tende a +∞ e si scrive
![]()
se comunque si scelga un numero H>0, a questo resta coordinato un numero
δ>0, tele che per ogni x dell'intorno xo :
|x-xo|<δ
eccettuato xo stesso si abbia f(x)>H.
In termini simbolici ![]()
In modo del tutto analogo si riesce a definire il limite a -∞ di una funzione per x che tende ad un valore finito
Si dice che la funzione f(x), per x che tende ad xo
tende a -∞ scrivendo
![]()
se, comunque si scelga un numero H>0, a questo resta coordinato un numero
δ tale che per ogni x dell'intorno di xo:
|x-xo|<δ
eccettuato xo stesso si abbia f(x)<-H.
![]()
● esempio 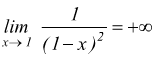
infatti qualunque sia H>0 si ha
 risolvendo
risolvendo 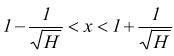
che costituisce un intorno di 1
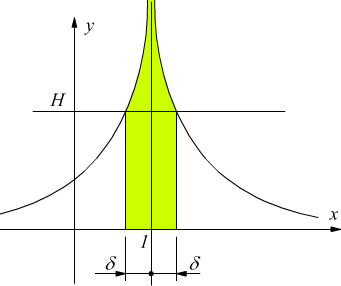
Limite finito per x che tende ad infinito
Si dice che la funzione y=f(x) tende al limite l
per x che tende a +∞ scrivendo
![]()
se comunque si scelga un numero ε>0 a questo resta coordinato
un numero xo tale che per ogni x>xo si abbia |f(x)-l|<ε.
![]()
Del tutto simile è la definizione per x che tende a -∞
● esempio 
In base alla definizione dobbiamo verificare se la disequazione
 ha
soluzioni e se queste costituiscono un intorno di +∞.
ha
soluzioni e se queste costituiscono un intorno di +∞.
La disequazione equivale a
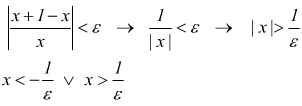
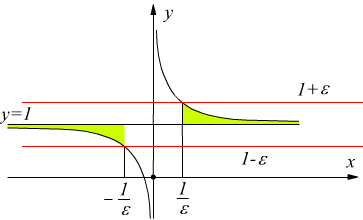
come si vede dal disegno la disequazione è soddisfatta perchè scegliendo un valore di x maggiore di $$x_o=1/ε$$, la y risulta compresa nell'intervallo (1, 1+ε) .
Limite infinito per x che tende a infinito
Si dice che la funzione y=f(x) per x che tende a +∞ tende a +∞
scrivendo
![]()
se comunque si scelga un numero H>0, a questo resta coordinato un numero
xo tale che per ogni x>xo si abbia f(x)>H .
![]()
Del tutto simili sono le definizioni per le altre eventuali scritture
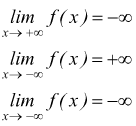
● esempio ![]()
dobbiamo verificare se la disequazione
![]() con
H>0 arbitrario, ha soluzioni, e se queste formano un intorno di +∞
con
H>0 arbitrario, ha soluzioni, e se queste formano un intorno di +∞
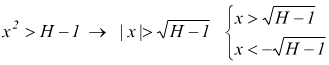
quindi posto ![]() per
ogni x>xo la disequazione è soddisfatta e il limite è verificato.
per
ogni x>xo la disequazione è soddisfatta e il limite è verificato.
Essa è soddisfatta anche per x<-xo; questo indica che se x
tende a -∞ la funzione tende a +∞.
Alla nozione di limite di una funzione matematica sono legati alcuni importanti teoremi.
Teorema dell'unicità del limite
Se per x tendente ad xo, la funzione y=f(x)
ha per limite il numero reale l allora tale limite è unico.
$\lim↙{x→x_o}f(x)=l$
La dimostrazione è condotta per assurdo, supponiamo infatti che sia $\lim↙{x→x_o}f(x)=l_1$ e $\lim↙{x→x_o}f(x)=l_2$ con $l_1≠l_2$ .
Se $l_1>l_2$ scegliamo arbitrariamente un valore $$ε={l_1-l_2}/2$$.
Per definizione di limite è possibile determinare un intorno di H1
di xo tale che per ogni x di tale intorno si abbia
 1
1
e un intorno H2 di xo tale che per ogni x di tale intorno si abbia
 2
2
Nella parte comune dei due intorni H1 ed H2 dovranno valere contemporaneamente la 1 e la 2 cioè le relazioni

ma ciò è assurdo. Quindi l1 non può essere diverso da l2. Il teorema rimane valido anche se il limite è infinito .
Teorema della permanenza del segno
Se è $\lim↙{x→x_o}f(x)=l$ con $l≠0$, allora esistono sempre intorni di xo (escluso al più xo)in cui la f(x) mantiene il segno del limite.
E' possibile dimostrare questo teorema supponendo che sia l>0. Data l'arbitrarietà nella scelta di ε, possiamo scegliere ε in modo che sia l-ε>0. Per definizione di limite resta determinato un intorno di xo , tale che per ogni x di tale intorno, escluso al più xo , si abbia
![]()
Questa relazione, essendo l-ε>0, dice che f(x) nell'intorno
considerato è positiva.
Se l<0, basta scegliere ε>0, in modo l+ε sia ancora
negativo. Viene allora individuato un intorno di xo , tale che
per ogni x di tale intorno, escluso al più xo si abbia:
![]()
Questa relazione, essendo l+ε<0 dice che f(x) nell'intorno considerato è negativa,
Teorema del confronto
Se le tre funzioni $y=f(x)$, $y=p(x)$ ed $y=q(x)$ sono
tali che in un intorno di xo (eccettuato al più xo
stesso) è sempre
$p(x)≤f(x)≤q(x)$
e se è
$\lim↙{x→x_o}p(x)=\lim↙{x→x_o}q(x)=l$
allora
è anche $\lim↙{x→x_o}f(x)=l$
Infatti, per definizione di limite, fissato ε>0 viene determinato un intorno H1 di xo , tale che per ogni x di tale intorno, escluso al più xo si abbia
![]()
Per lo stesso valore di ε esiste un intorno H2 di xo , tale che per ogni x di tale intorno (escluso al più xo) si abbia
![]()
Nella parte comune dei due intorni H1 ed H2 le due limitazioni valgono contemporaneamente. Quindi si ha
![]()
Si conclude che per tutti gli x dell'intorno stesso (eccettuato al più xo) si ha
![]() che
equivale a dire $\lim↙{x→x_o}f(x)=l$
che
equivale a dire $\lim↙{x→x_o}f(x)=l$
Il teorema rimane valido anche se il limite è infinito.
Funzioni continue
Abbiamo visto che nel caso del limite per x che tende ad xo di una funzione, non è necessario che xo appartenga al dominio della funzione, ma ciò che accade nel punto xo , se esso appartiene al dominio D è del tutto ininfluente, quello che conta è come si comporta la funzione "vicino" a xo e a quale valore si avvicina, non "quanto vale" in xo.
E' la nozione di continuità che pone
in relazione $\lim↙{x→x_o}f(x)$ con
f(xo); quindi, per parlare di questa proprietà, non solo xo
deve essere punto di accumulazione per l'insieme D di definizione di f(x),
ma xo deve anche appartenere al dominio D.
La definizione formale di continuità di una funzione è la seguente.
Una funzione y=f(x) definita nel dominio D si dice
continua nel punto xo se
$\lim↙{x→x_o}f(x)=f(x_o)$
in via preliminare, devono, comunque essere verificate le seguenti tre
condizioni
1 la funzione deve essere definita in xo
2 deve esistere il limite per x → xo
3 tale limite deve essere uguale ad f(xo)
Quando anche una sola delle tre condizioni suddette non è soddisfatta si dice che la funzione f(x) è discontinua in xo.
E' possibile affermare la continuità della funzione y=f(x) nel punto xo
anche se esistono i suoi limiti destro e sinistro per
x → xo
ed essi valgono xo.
![]()
Inoltre se vale solo la relazione
$\lim↙{x→x^{+}_o}f(x)=f(x_o)$ oppure solo la relazione $\lim↙{x→x^{-}_o}f(x)=f(x_o)$
si parla rispettivamente di continuità destra oppure sinistra in xo.
Oltre alla definizione di continuità puntuale (in un punto) è possibile dare anche una definizione di continuità in un intervallo (chiuso).
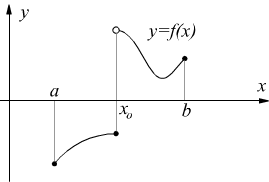
Si dice che una funzione y=f(x) è continua nell'intervallo [a, b] se è continua nei punti interni dell'intervallo e continua alla destra dell'estremo a e a sinistra di b.
Tramite vari esempi è possibile riconoscere che esistono tre diversi tipi di discontinuità.
a Discontinuità di prima specie
Nel punto xo la funzione f(x) presenta una discontinuità di prima specie quando in tale punto esistono finiti i due limiti destro e sinistro, ma sono tra loro diversi cioè quando
![]()
con l1 ≠ l2 . La differenza |l1-l2| è chiamato salto della funzione in xo.
Ad esempio la funzione  che
è definita ∀x ≠ 0.
che
è definita ∀x ≠ 0.

Non esistendo f(0) la funzione non è continua in x=0 ed essendo
![]()
il punto x=0 è una discontinuità di prima specie.
b Discontinuità di seconda specie
Nel punto xo la funzione f(x) presenta una discontinuità di seconda specie quando in quel punto almeno uno dei due limiti sinistro o destro non esiste o se esiste è infinito.
Ad esempio la funzione $$y=1/x$$ ha una discontinuità di seconda specie nel punto x=0, perchè

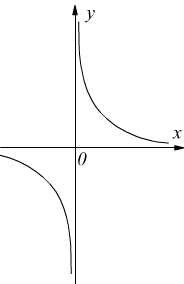
c Discontinuità di terza specie (o eliminabile)
La funzione y=f(x) presenta in xo una discontinuità di terza specie quando esiste finito il limite
$\lim↙{x→x_o}f(x)$
ma la funzione f(x) non è definita in xo oppure lo è ma risulta $\lim↙{x→x_o}f(x)≠f(x_o)$
Ad esempio consideriamo la prima funzione che abbiamo analizzato in questa pagina
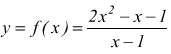
il dominio è D ≡ R-{ 1 } la funzione è discontinua in xo=1 perchè f(1) non esiste ma
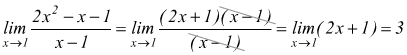
Per la definizione di limite, possiamo dire che, scelto un intorno completo di xo=1 sempre più ristretto, la funzione assume valori sempre più vicini a 3 e quindi possiamo dire che la funzione è quasi continua perchè rimane escluso solo il punto xo=1.
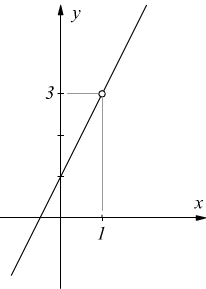
Il punto x=1 viene anche detto di discontinuità eliminabile perchè la funzione
può essere modificata (ridefinita) nel punto 1 in modo da renderla continua
facendo rimanere invariato il suo dominio naturale:
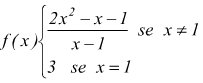
Proprietà delle funzioni continue
Le funzioni continue sono caratterizzate da alcune importanti proprietà che bisogna ricordare.
Teorema della funzione composta
Se f(x) e g(x) sono due funzioni continue, tali che esista, per x appartenente ad un intervallo A, la funzione composta F(x)=g[f(x)] allora la funzione F(x) è pure continua. Ad esempio sono continue ∀x reale le funzioni :

Teorema della funzione inversa
Se una funzione è continua in un intervallo A e in quest'intervallo ammette la funzione inversa, allora anche la funzione inversa è continua. Sono ad esempio continue le inverse delle funzioni circolari:
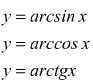
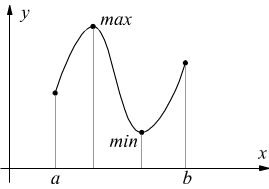
Teorema di Weierstrass
Se una funzione y=f(x) è continua in un intervallo chiuso [a, b], allora allora essa assume, in tale intervallo, il massimo assoluto e il minimo assoluto.
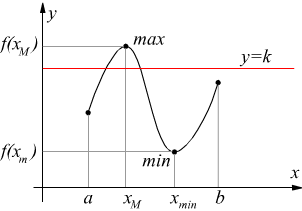
Teorema dei valori intermedi
Se y=f(x) è una funzione continua in un intervallo chiuso [a, b] all'ora essa assume almeno una volta tutti i valori compresi tra il massimo ed il minimo. riferendoci al seguente disegno, il teorema equivale a dire che la retta y=k con f(xm) < k < f(xM) incontra il grafico di f(x) almeno una volta.
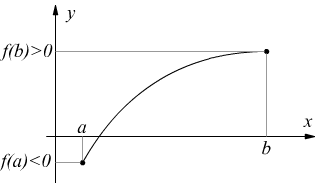
Teorema degli zeri
Se una funzione, continua in un intervallo chiuso [a, b] assume agli estremi a e b valori di segno opposto, essa si annulla almeno in un punto dell'intervallo.
una funzione discontinua nel punto xo di un determinato intervallo [a, b] può non rispettare il precedente teorema: come si vede dal seguente disegno in nessun punto dell'intervallo [a, b] la funzione si annulla.
 edutecnica
edutecnica