Sommatori binari
L’addizione è la più elementare delle operazioni aritmetiche; l’addizione
è più o meno la sola cosa che i computer fanno; l’unico problema è riuscire
a costruire qualcosa che produca delle somme col sistema binario, dato che
tutte le macchine sono basate su questo sistema numerico.
Sommare numeri binari è più o meno come sommare numeri decimali, per sommare
due numeri come 245 e 673, si scompone il problema in passi più semplici.
Ogni passo richiede soltanto di sommare una coppia di cifre decimali. In
questo esempio si comincerebbe con 5 più 3 (etc.).
I sommatori binari sono reti combinatorie che ricevono
in ingresso n bit degli addendi da sommare e generano in uscita i bit della
somma binaria con il relativo riporto.
Si tratta, dunque, di un tipico esempio di rete combinatoria con ingressi
multipli ed uscite multiple, strutturata in modo da seguire il meccanismo
secondo cui avviene la somma binaria.
Introduciamo, pertanto, i due blocchi funzionali fondamentali che sono:
• il semisommatore binario HA (Half Adder) senza riporto in ingresso
;
• il sommatore binario FA (Full Adder) con riporto in ingresso.
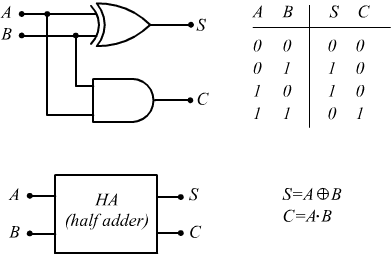
Circuito semisommatore HA
La differenza tra la somma in decimale e la somma in binario è che per
quest'ultimo sistema lo schema per la somma è molto più semplice:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 con riporto 1
questo schema non è altro che la tabella della verità della porta XOR (a parte la questione del riporto che deve essere risolta).
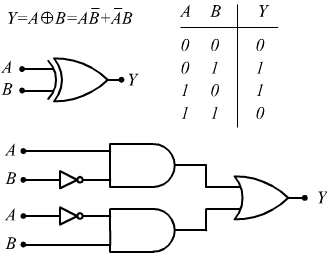
Per gestire anche il riporto questo circuito deve essere modificato in modo da risolvere la seguente tabella della verità
Dove A e B sono i bit da sommare, S è il bit della somma (sum) e C è il
bit del riporto (carry).
Abbiamo così costruito il semisommatore o Half-Adder.
Circuito sommatore FA
Il dispositivo creato si chiama semi-sommatore (half-adder) questo nome deriva dal fatto che per ottenere la somma completa (full-adder) tra due numeri di più cifre, oltre ai bit dello stesso ordine occorre sommare anche il riporto eventualmente ottenuto dai due bit di ordine immediatamente inferiore.
Per questo motivo il circuito full-adder si presenta con tre ingressi e due uscite.
I due ingressi sono costituiti dai due bit An e Bn
da sommarsi e dal riporto Ci eventualmente ottenuto dalla somma
dei due bit An-1 e Bn-1 .
Le due uscite sono composte dal bit di somma dei tre ingressi e dall'eventuale
riporto Co da inviare al full-adder successivo. Qui sotto è mostrato
il simbolo logico, la tabella della verità e lo schema circuitale di un
full-adder
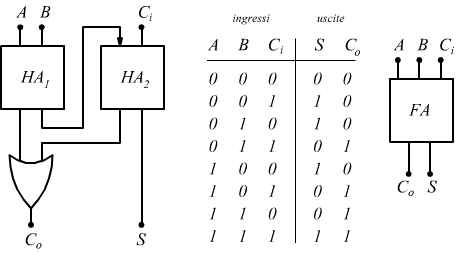
Dalla tabella della verità è possibile dedurre la funzione logica della somma eseguita di questo circuito combinatorio

mentre la funzione logica del riporto è la seguente
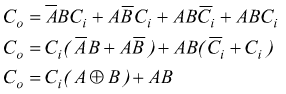
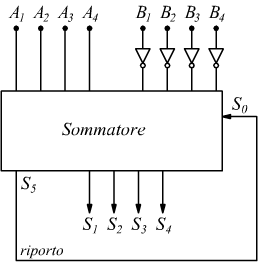
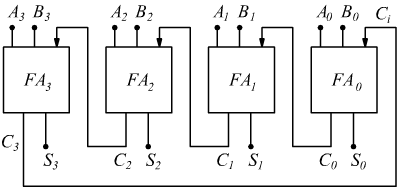
Quando si vogliono sommare numeri di più bit ciascuno, il metodo più semplice è quello di realizzare un sommatore parallelo come disegnato qui
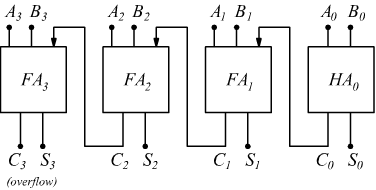
mettendo in cascata tanti FA (full-adder) quanti sono i bit di ciascun
numero binario da sommare.
Se per ipotesi usiamo dei nibble (4bit) i quattro bit di ciascun numero
vengono presentati simultanemente all'ingresso del full-adder e viene effettuata
la somma se non è presente alcun riporto.
Nel caso peggiore, invece, in cui ad ogni somma corrisponde un riporto,
si avrà che questo bit traslerà dal primo HA a tutti gli altri FA fino all'ultimo.
A :
B :
E' molto facile schematizzare il comportamento del sommatore anche usando l'excel.
Qui sotto è riportato lo schema completo di un addizionatore a 4 bit che usa solo porte elementari ed in cui i numeri da sommare sono individuati dalle posizioni degli otto deviatori (considerando +Vcc=1 e GND=0).
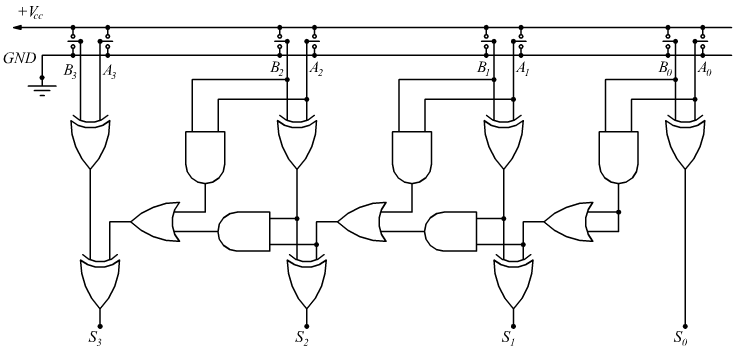
Sottrattori binari
In analogia a quanto visto per il sommatore, è possibile realizzare una rete combinatoria che realizza una sottrazione tra due numeri binari; anche in questo caso, tenendo presenti le regole della sottrazione binaria, dobbiamo preparare due blocchi fondamentali:
˙ il semisottrattore binario HS (Half subtracter) senza prestito in
ingresso
˙ il sottrattore binario FS (Full subtracter) con prestito in ingresso
.
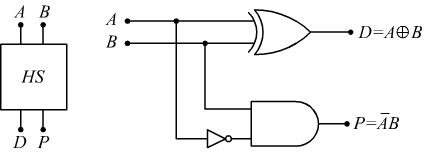
Circuito semisottrattore HS
Il semisottrattore è il blocco elementare che realizza la differenza di due bit: deve rispettare la seguente tabella della verità
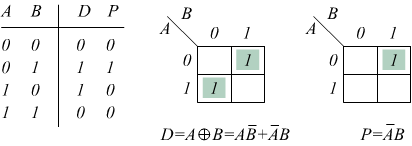
In questo caso invece che usare i teoremi dell'algebra di Boole semplifichiamo la funzione con le mappe K ottenendo come variabili di uscita.
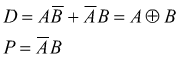
La differenza si ottiene facendo l'operazione di XOR (EX_OR o OR esclusivo) come nel caso del sommatore, mentre il prestito è un AND logico tra la variabile B e la variabile A negata.
Circuito sottrattore FS
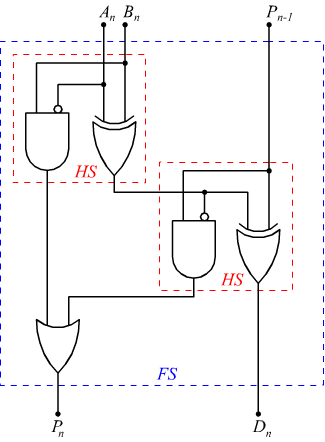
Lo schema completo di un sottrattore è qui riportato, dove
An ; Bn sono i bit da sottrarre
Pn è il prestito da richiedere
Dn è la differenza binaria
Pn-1 è il prestito da fornire
Il circuito logico che esegue la sottrazione è ottenuto sviluppando la
funzione in due fasi: dapprima, con un HS si sottraggono An e
Bn ; successivamente, mediante un secondo HS si toglie il riporto
Pn-1 . I riporti in uscita convergono verso una porta OR.
In modo analogo al sommatore non si verifica mai che a questo porta si presentino
due 1 simultaneamente.
Per eseguire la sottrazione binaria di due numeri di n bit, bisogna disporre
di n blocchi elementari, coi prestiti connessi in cascata. Il primo blocco,
meno significativo, non avendo riporto in ingresso, può essere un HS, gli
altri saranno necessariamente degli FS.
Bisogna dire che in caso di calcoli complessi, i sottrattori sono poco usati. Si preferisce effettuare l'operazione tramite una addizione con complementazione.
In tal caso, l'operazione aritmetica di sottrazione viene effettuata aggiungendo al minuendo il complemento a uno del sottraendo. Il sottrattore è, in questo caso, simile ad un sommatore al quale uno dei due numeri giunge complementato
e l'eventuale riporto, ottenuto dalla somma dei bit significativi, deve essere aggiunto alla somma dei bit meno significativi. Si deve osservare che il riporto si ha solo nel caso in cui il minuendo è maggiore del sottraendo e mai nel caso opposto.
caso A minuendo maggiore del sottraendo

caso B minuendo minore del sottraendo

In quest'ultimo caso già sappiamo che il risultato è negativo come segno perchè minuendo < sottraendo poi basta prendere il risultato 1100 e complementarlo nuovamente a 1 per conoscere il modulo del numero. che è (0011)2=(3)10.
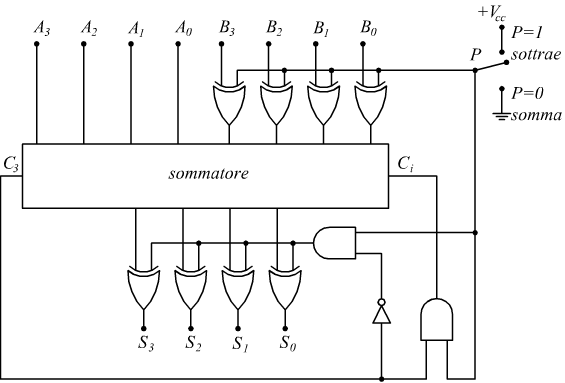
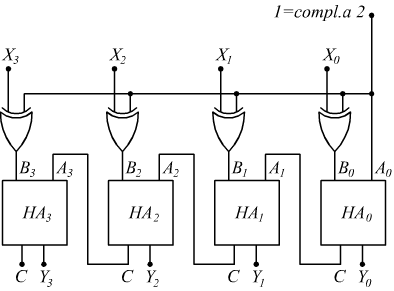
Il circuito da realizzare deve quindi essere in grado di complementare eventualmente un addendo e poi deve tener conto del riporto causato dalla somma dei due bit più significativi. Partendo da un sommatore semplice, un circuito capace di eseguire la sottrazione con il metodo del complemento ad 1 può essere schematizzato dal seguente disegno.
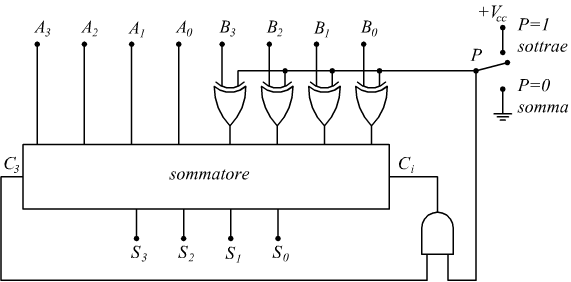
L'uscita C3 costituisce il riporto eventuale ottenuto dalla somma di A3 e B3 mentre C0 è l'ingresso che deve essere sommato ad A0 e B0.
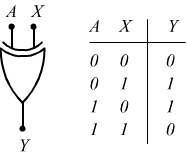
Per fare in modo che il circuito possa funzionare da sommatore o da sottrattore
occorre dotarlo di un comando che complementi o non complementi uno dei
due nibble, ed inoltre impedisca o no la somma dell'ultimo riporto con i
bit meno significativi.
Dallo schema si riconosce come l'operazione di complementazione ad 1 possa
essere eseguita su un singolo bit da una porta XOR.
Si vede come quando la variabile X=1 la variabile A venga commutata (complementata
ad 1) mentre quando X=0 la variabile A non venga complementata.
La variabile X applicata ad ogni singolo bit del sottraendo B sarà determinata
dalla posizione del selettore P.
L'eventuale bit di riporto C3 dovrà coincidere con il riporto
in ingresso Ci associato ai due bit meno significativi; si deduce
che il dispositivo è costituito da 4 FA e non da 3 FA e un HA sul LSB come
nel sommatore puro.
rimane solo una correzione da fare; nel caso in cui l'operazione sia una sottrazione (P=1) ed il risultato sia eventualmente negativo (C3=0) deve essere eseguita una complementazione su quest'ultimo. Questo può essere effettuato con la stessa struttura di porte prevista sull'operando B.
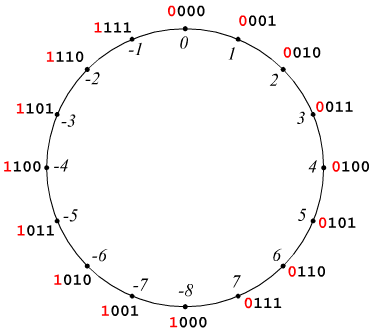
Abbiamo precedentemente
detto che solitamente nei sistemi digitali i numeri interi relativi vengono
rappresentati con il metodo del complemento a 2, utilizzando il bit più
pesante come bit di segno:
0=numero positivo
1=numero negativo
quindi in un sistema a 4 bit avremo le seguenti eventualità
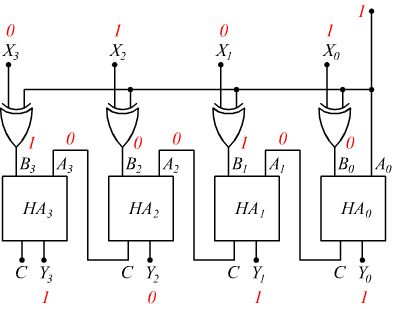
I circuiti sommatori sono indispensabili anche in questo caso. Il circuito
disegnato sotto ci permette di eseguire il complemento a 2 di un numero
a 4 bit.
Se il terminale A0=1 si ha la complementazione a 2 dei bit in
ingresso X che saranno rappresentati dai bit Y in uscita ; se A0=0
il numero rimane invariato(X3X2X1X0=Y3Y2Y1Y0).
Supponiamo infatti di voler complementare il numero +5=0101, dopo aver posto A0=1 ecco cosa accade
infatti 1011=-5. Se teniamo conto che nel sistema binario con rappresentazione
a complemento a 2, la differenza tra due numeri positivi avviene complementando
a 2 il sottraendo e poi sommando quest'ultimo valore al minuendo.
Il dispositivo precedente può anche essere facilmente usato per ricavare
il modulo del numero in ingresso, se infatti siamo in presenza di un numero
negativo il bit X3 può pilotare l'ingresso di complementazione
A0. Supponiamo, infatti di voler calcolare il modulo di 1101C2
basterà porre X3=A0.
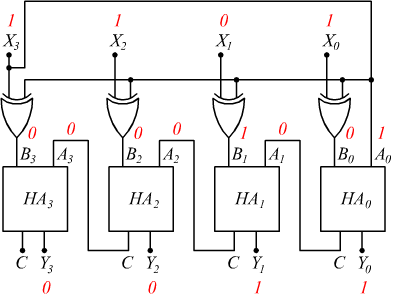
Infatti 1101C2=-3 con |-3|=3=0011C2.
Supponiamo di voler effettuare l'operazione A±|B| con A numero naturale
positivo e B numero positivo in complemento a 2. Ipotizzando di operare
sempre in un sistema di 4 bit possiamo collegare i dispositivi precedenti
nel seguente modo.

Una volta implementata la sottrazione abbiamo di fatto realizzato una unità aritmetico-logica, dato che la moltiplicazione non è altro che una somma ripetuta e la e la divisione , a sua volta, una sottrazione ripetuta.
Display a 7 segmenti
La realizzazione di dispositivi numerici digitali si accompagna alla necessità di visualizzazione di variabili e di risultati. In Particolare, nel caso dei circuiti sommatori e sottrattori si può ricorrere ai display a 7 segmenti a diodi LED (Light emitting Diode) oppure a cristalli liquidi LCD (Liquid Crystal Display). In entrambi i casi i segmenti utilizzati vengono identificati secondo il seguente schema

I display a 7 segmenti devono essere guidati da un opportuno decoder per effettuare la rappresentazione in decimale di un codice BCD (Binary Code Decimal) che è un codice a 4 bit, ottenuto utilizzando le prime 10 cifre del binario puro assegnandole alle corrispondenti cifre del decimale secondo la seguente orditura
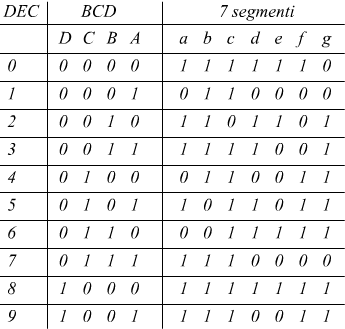
Si osserva che nel codice BCD le combinazioni 1010, 1011, 1100, 1101, 1111 sono inutilizzate ( ridondanti ) e prive di significato.
Se assumiamo che nella sequenza dei bit in ingresso la cifra più significativa sia D (MSB=Most significant Bit) mentre la cifra meno significativa sia A (LSB=Least Significant Bit) si avrebbe il seguente collegamento:

La struttura interna del decodificatore (che normalmente si acquista dal mercato) può facilmente essere ricavata costruendo la mappa di Karnaugh per ciascuna delle sette variabili di uscita a,b,c,d,e,f,g ottenendo le seguenti semplificate espressioni
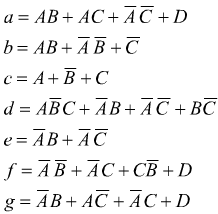
Nell'attuare questo procedimento, i cinque numeri inutilizzati dal codice BCD possono essere considerati condizioni di indifferenza.
Se invece i vuole mantenere la codifica in ingresso in binario puro, allora saranno ammesse anche le combinazioni di bit precedentemente escluse, ma l'unica maniera per utilizzarle sarà quella di interpretare l'uscita secondo una codifica esadecimale da (0)10=(0000)2=(0)H a (15)10=(1111)2=(F)H.
 edutecnica
edutecnica