Aritmetica binaria
Dopo aver parlato del sistema
numerico binario, vediamo adesso, come applicare in questo sistema le
operazioni aritmetiche fondamentali.
Le regole dell'aritmetica binaria sono del tutto simili alle regole che
presiedono l'aritmetica del sistema decimale.
Addizione con numeri binari
Se chiamiamo A e B i due bit da sommare dobbiamo solo far riferimento alla presente tabella, dove con S indichiamo la somma e con R (carry) il riporto dei due bit

in tal modo nel sistema binario risulterà 1+1=10(2)=2(10). Per eseguire la somma di due numeri binari si devono sommare le cifre bit a bit tenendo conto del riporto, se chiamiamo A e B i due addendi, proviamo ad eseguire la somma 1001+1101 cioè 9+13.

Come si vede, si applica lo stesso metodo del sistema numerico decimale che ci ha insegnato la maestra delle elementari. Si procede incolonnando i due addendi A e B è, partendo da destra, si eseguono ordinatamente le operazioni di somma S e riporto R, collocandolo in testa alla colonna adiacente di sinistra.

nel caso in cui si abbia 1+1+1 si avrà S=1,
R=1.
Sottrazione con numeri binari
Vediamo adesso il caso della sottrazione binaria in cui il minuendo sia maggiore del sottraendo e quindi la differenza positiva. In tal caso si può seguire la tabella qui riportata dove con D indichiamo la differenza tra i due bit e con P il prestito (borrow).
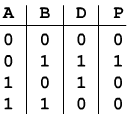
Il prestito P, è preso, come nel caso decimale, dalla cifra precedente del minuendo; nel caso quindi che questa sia 1 diventerà 0. Vediamo un esempio, indicando con A il minuendo e con B il sottraendo, eseguendo la sottrazione 1100-0110.

Si procede nel modo seguente: si incolonnano i due numeri A e B e, partendo da destra, si eseguono ordinatamente le operazioni di sottrazione D e di prestito P, collocandolo in testa alla colonna adiacente di sinistra, Si ha così
1a colonna : 0-0=0 →
D=0, P=0
2a colonna : 0-1; in questo
caso si prende a prestito dalla colonna adiacente sinistra P=1 che, riferito
alla colonna di destra vale 10=2. L'operazione diventa 2-1=1 → D=1
P=1
3a colonna : si toglie il prestito
al corrispondente bit del minuendo , 1-1=0; si toglie ora, dal risultato,
il sottraendo: 0-1. Per effettuare questa operazione si ricade nel caso
illustrato nella seconda colonna ottenendo: D=1, P=1.
4a colonna : in modo analogo
alla terza colonna, eseguendo le medesime operazioni bit a bit si ha :
1-1=0
0-0=0 → D=0, P=0
Si nota pertanto, che le cifre che hanno un trattino sopra di esse si
devono considerare 0 a causa del riporto.
Se invece la cifra del minuendo, da cui si prende il prestito, vale 0 allora
questa diventerà 1 ed il prestito scivolerà sulla cifra che la precede,
e così di seguito finchè non si tova un 1. Altro esempio 1000-0011
:

le cifre sovrascritte da un trattino si devono considerare 1 a causa del riporto.
Se il minuendo è minore del sottraendo questa procedura risulta ancora
più difficoltosa; bisogna poi tener conto che i sistemi digitali sono in
grado di implementare solo la somma ed il complemento. Per questo motivo
la sottrazione binaria deve essere eseguita usando queste due ultime funzioni
opportunamente combinate.
Distanza tra due numeri binari
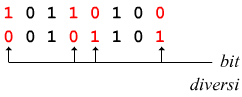
La distanza tra due numeri binari che abbiano lo stesso numero di cifre è definita come il numero di bit per i quali i due numeri differiscono. Ad esempio 1011 e 1101 hanno distanza 2 infatti

10110100 e 00101101 hanno distanza 4 infatti
Complemento a 1
Quando la distanza tra due numeri binari è massima, cioè tutti gli 1 sono
cambiati in 0 e viceversa, i due numeri si dicono complementari con complemento
a 1. Ad esempio 0110 e 1001
sono complementari. 1101101 e 00100100
sono due byte complementari.
Complemento a 2
Questa operazione, nonostante sia poco frequentemente applicata è già nota dall'aritmetica decimale, infatti il complemento Nc a 10 di un numero decimale N(10) è definito come
![]()
dove n rappresenta il numero di cifre di N(10).
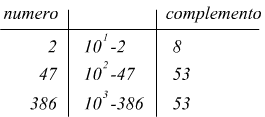
In modo analogo al complemento a 10 si può definire il complemento a 2 di un numero binario N(2).
![]()
dove n è il numero di cifre di N(2).
Calcoliamo ad esempio il complemento a 2 di 101. Con n=3 e 2n=23=8(10)=1000(2) poi eseguiamo la sottrazione
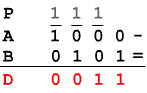
il complemento a 2 di un numero binario si può ottenere anche attraverso ad un'altra procedura, evitando di eseguire, in questo modo, la sottrazione.
1 si esegue il complemento ad 1 del numero
dato
2 si aggiunge 1 al numero così ottenuto
rifacendoci al caso precedente
![]()
Sottrazione binaria con il complemento a 2
Adesso siamo in grado di eseguire la sottrazione binaria come una somma tra il minuendo ed il complemento a 2 del sottraendo, si possono individuare due casi.
● Minuendo maggiore del sottraendo : risultato positivo
1 Prendiamo il sottraendo con lo stesso numero
di cifre del minuendo se necessario aggiungendo degli zeri davanti al MSB
ed eseguiamo il complemento a 2 del numero
2 Sommiamo quanto ottenuto al passo precedente
al minuendo e non consideriamo il MSB del risultato .
Esempio 14-5=9 cioè 1110-0101.
0101 → (1010)' →
(1011)"
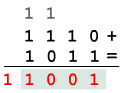 risultato
1001(2)=9(10)
risultato
1001(2)=9(10)
Esempio 45-26=19 cioè 101101-011010 eseguiamo il
complemento a 2 sul sottraendo.
011010 → (100101)' →
(100110)" eseguiamo l'addizione:
 risultato
10011(2)=19(10).
risultato
10011(2)=19(10).
● Minuendo minore del sottraendo, risultato negativo
1 prendiamo il sottraendo e sottoponiamolo
al complemento a 2
2 sommiamo quanto ottenuto al minuendo e consideriamo
anche il MSB
3 eseguiamo al contrario il complemento a 2
sul risultato ottenuto
Esempio: 4-6=-2 cioè 100-110.
110 → (001)' → (010)"
 adesso
complementiamo a 2 il risultato
adesso
complementiamo a 2 il risultato
110 → (001)' → (010)"
Esempio : 25-43=-18 cioè 011001-101011.
101011 → (010100)' →
(010101)"
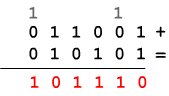 eseguiamo
il complemento a 2 del risultato
eseguiamo
il complemento a 2 del risultato
101110 → (010001)'
→ (010010)"
il risultato sarà negativo in modulo pari a 10010(2)=18(10).
Moltiplicazione binaria
La moltiplicazione binaria si esegue con le stesse regole di quella decimale, basta ricordare la tabella del prodotto M a due bit qui riportata.
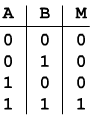
Ad esempio eseguiamo M=1101·101 cioè 13·5=65

Notiamo che nel caso dei numeri binari basta considerare solo gli 1 del moltiplicatore, perchè gli zeri eseguono solo uno spostamento a sinistra della cifra successiva.
Esempio : M=1011·1001 cioè 11·9=99.

Divisione binaria
Anche per la divisione binaria valgono le regole della corrispondente
divisione decimale, col vantaggio che il quoziente può essere soltanto 1
o 0.
Esempio 21:7=3

Si tratta, in sostanza, di eseguire delle sottrazioni successive con il
corretto incolonnamento.
Rappresentazione in modulo e segno
Sappiamo che con n bit è possibile esprimere 2n numeri da 0 a 2n-1 . Nel caso in cui si debbano elaborare numeri relativi, è necessario introdurre una ulteriore informazione relativa al segno + o -. E' possibile usare una rappresentazione detta in modulo e segno, il cui il bit più significativo appare come il bit di segno, precisamente 0 per i numeri positivi e 1 per i numeri negativi. Il campo dei numeri relativi che si possono esprimere in un sistema ad n bit risulta
![]()

nel disegno sopra viene riportata la numerazione
in modulo e segno per un sistema a 4 bit (-7 ≤ Nr ≤
7 ) notiamo la presenza di due valori per lo zero (0000 e 1000) questo fatto
comporta nei sistemi di elaborazione digitale una maggiore complicazione
circuitale, per cui si preferisce ricorrere ad una rappresentazione dei
numeri relativi utilizzando il complemento a 2.
Rappresentazione in complemento a 2
Ricorrendo alle proprietà sul complemento già viste, possiamo esprimere i numeri positivi nel modo usuale, facendoli precedere da uno 0, mentre i numeri negativi si possono esprimere come il complemento a 2 del corrispondente numero positivo. Come si vede dal disegno il MSB dei numeri negativi è sempre 1.

La rappresentazione in complemento a 2 permette di esprimere un campo di escursione per i numeri relativi Nr che vale
![]()
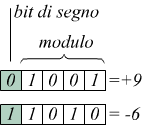
Ad esempio se il sistema ha 5 bit il bit più pesante (a sinistra) viene usato per indicare il segno del numero. La convenzione prevede che il bit di segno sia 0 per i numeri positivi e sia 1 per i numeri negativi.
si vede come il secondo numero sia sicuramente negativo, perchè MSB=1 ma il suo valore può essere dedotto solo facendo il complemento a 2 del modulo, 1010 → (0101)' → (0110)" cioè 110(2)=6(10). Quindi il numero è negativo e il suo valore in modulo è 6; cioè stiamo parlando di -6.
Un altro modo abbastanza veloce per trovare il valore decimale di un numero binario ad n bit, complementato a 2 è utilizzare la formula
![]()
applicata al caso precedente
![]()
![]()
nel caso di un sistema ad 8 bit si ha
![]()
La somma algebrica eseguita con questa rappresentazione, porta sempre
a risultati corretti purché si ignori l'eventuale bit di riporto. Naturalmente
nell'esecuzione delle operazioni è necessario rimanere nel campo limite
dei numeri Nr in caso contrario occorre passare ad una rappresentazione
con un numero maggiore di bit.
Numeri reali in virgola mobile
La rappresentazione dei numeri reali in virgola mobile (floating point) viene chiamata anche notazione scientifica, ad esempio N = -1,853·103 è un numero scritto con notazione scientifica; si possono individuare tre elementi:
● il segno -
● la mantissa 1,853
● l'esponente 3
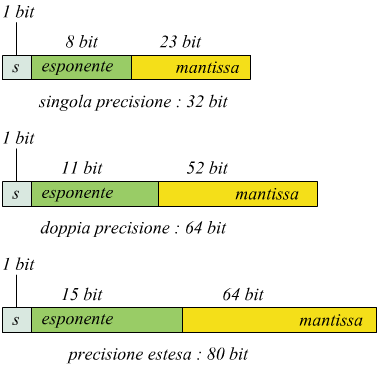
Attualmente, il formato di rappresentazione dei numeri reali in virgola mobile è definito dallo standard IEEE 754 che ha la seguente struttura
![]()
dove s indica il segno 0 per i numeri positivi (+); 1 per i negativi(–). Lo standard riconosce tre formati
● singola precisione
● doppia precisione
● precisione estesa
I numeri reali in virgola mobile si possono allora esprimere attraverso i seguenti formati
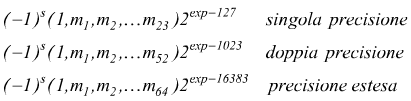
Nel campo mantissa, si vede come il valore 1 sia sempre sottinteso sul primo bit, esso non viene memorizzato nella singola e nella doppia precisione mentre viene memorizzato nel formato a precisione estesa. La parte decimale successiva si ottiene moltiplicando i bit per potenze decrescenti del 2 a partire da 0
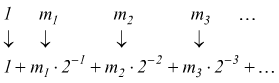
ottenuta la mantissa nella forma 1,xxx10 è suffficiente moltiplicare tale numero per 2exp-127
![]()
per ottenere il numero in virgola mobile (floating point) in formato a precisione singola.
In alternativa possiamo lasciare la mantissa nel suo formato binario per poi farla slittare di un numero di cifre pari all'esponente e=exp-127 ad esempio
![]()
per poi convertire tale numero in decimale. Un esempio concreto è il seguente: convertiamo in decimale il numero in virgola mobile
0 10000001 11110000000000000000000
s=0=+
exp : 100000012=129
e=129-127=+2
m=(1)+2-1+2-2+2-3+2-4=1,9375
N=1,9375(10)·22=7,75
seguendo un procedimento alternativo si può notare che la mantissa vale
(1,1111)2·22 = 111,112
= 22+21+20+2-1+2-2 =
4+2+1+0,5+0,25=+7,75
E possibile anche eseguire la conversione inversa da numero decimale a formato binario -300,25=NFP?
N10=100101100,01=1,0010110001·28
s=1= –
e=8 exp=127+8=135=10000111
m=1,0010110001 → 0010110001
NFP=1 10000111 00101100010000000000000
Nel seguente modulo è possibile inserire un numero in formato decimale per ottenere la sua rappresentazione binaria nello standard IEEE 754 a precisione singola.
 edutecnica
edutecnica