Piano inclinato

     

Il piano inclinato è una macchina semplice che può essere ottenuta appoggiando un corpo rigido sopra una superficie inclinata di un prefissato angolo rispetto all'orizzontale.
Il contatto fra le superfici del corpo appoggiato può essere caratterizzato da attrito, oppure no; in quest' ultimo caso si parla di vincoli lisci.
Ipotizziamo per semplicità la situazione disegnata in figura, dove un parallelepipedo dotato di massa m e quindi di peso p=mg venga appoggiato al piano inclinato che qui immaginiamo privo di attrito.

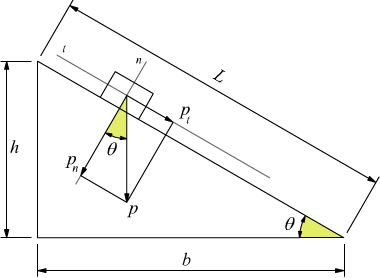
Decomponiamo il vettore forza peso [p] secondo le direttrici normale [n] e tangenziale [t] al piano, passanti per il baricentro del corpo rigido ottenendo i due vettori p_n e p_t.

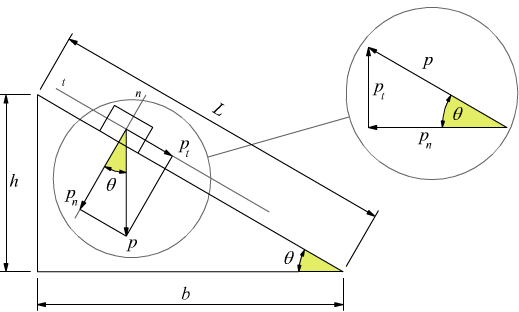
Possiamo anche non sapere o non ricordarci niente di trigonometria, l'importante è osservare che il triangolo di lati
b-h-L è simile al triangolo di lati p_n-p_t-p, come evidenziato; questo ci permette di impostare la proporzione:

         

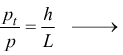
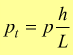
Se invece si vuole tener conto della trigonometria, basta osservare che

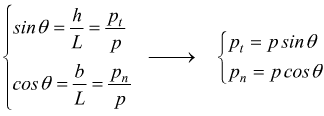
Quando un corpo è semplicemente appoggiato ad un piano, la reazione vincolare N di questo è sempre perpendicolare al piano stesso.

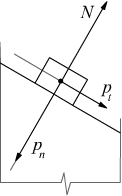
Se immaginiamo il corpo rigido descritto come un punto materiale, identificabile col suo baricentro in cui sia concentrata tutta la forza peso notiamo come la componente p_n normale al piano sia compensata dalla reazione vincolare N mentre la componente tangenziale al piano p_t non è compensata da niente. Da qui si deduce che se non ci sono forze che vanno ad equilibrare la p_t questa forza tende a far scendere il corpo lungo il piano.

Le possibili forze che possono compensare p_t sono
a) la forza di attrito tra il piano ed il grave
b) una forza equilibrante esterna applicata al grave

Quando non vi è attrito, si parla esplicitamente di vincolo liscio. Quando vi è attrito, deve essere assegnato f=coefficiente di attrito. Se si ragiona semplicemente su un corpo rigido appoggiato ad un piano orizzontale

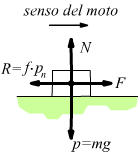La forza di attrito si calcola moltiplicando la forza attiva perpendicolare al piano di appoggio per il coefficiente di attrito.
In questo caso la forza attiva verticale coincide con la forza peso p, quindi R=f·p ne consegue che per muovere orizzontalmente il corpo in questione bisogna applicare una forza F ≥ R.
Bisogna fare attenzione al fatto che la forza di attrito si manifesta sempre in senso contrario alla direzione dello spostamento.
Se il corpo è inizialmente fermo si parla di coefficiente di attrito statico [f_s] mentre quando lo stesso oggetto è già in moto bisogna considerare il coefficiente di attrito dinamico [f_d] chiaramente risulta f_s > f_d.

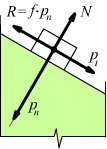
Nel caso specifico del piano inclinato la forza normale al piano è p_n essa genera una forza di attrito R=f_s·p_n; si conclude che finchè

     il corpo resta fermo.

Quando questa condizione non è più vera, il corpo si mette il movimento lungo il piano.

Bisogna precisare che quando si parla di forza attiva verticale si intende la forza attiva netta. Ad esempio se su un piano orizzontale oltre alla forza peso p agisce anche una seconda forza T la forza attiva netta che agisce in direzione verticale coincide con N=p-T_y dunque :

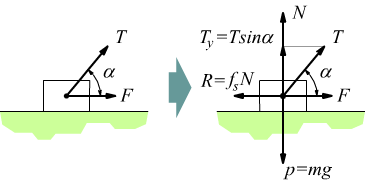
La forza attiva verticale nel casi di un corpo appoggiato coinciderà sempre con la reazione vincolare di quel corpo che per definizione è perpendicolare al piano stesso.

E' facile tradurre questa eventualità anche nel caso di un grave collocato su un piano inclinato:

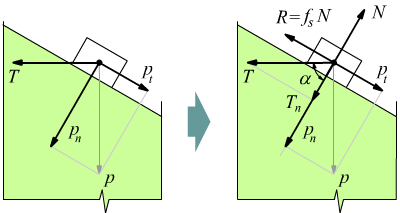
in questo caso le forze attive applicate in direzione perpendicolare all'appoggio sono p_n e T, quest'ultima ha evidentemente una componente in direzione normale contro il piano di appoggio, cospirante con p_n che vale T_n=Tcosα. La somma algebrica di queste due forze coincide con la reazione vincolare N.

In generale, per calcolare la forza di attrito è più corretto considerare la reazione vincolare normale al piano di appoggio (N) intesa come equilibrante delle forze attive agenti in direzione perpendicolare al piano stesso.

Cinematica del piano inclinato

     

Quando si considera un problema col piano inclinato è inevitabile decomporre la forza peso secondo le due direzioni normale e tangenziale al piano stesso.
La componente normale è compensata dalla reazione vincolare N uguale e contraria al piano stesso.
La componente normale p_n è poi coinvolta nella generazione della forza di attrito R=f·p_n che si oppone al moto del corpo che si trova sul piano.
La componente tangenziale al piano p_t è invece responsabile dello scivolamento verso il basso che può eventualmente instaurarsi (dipende dall'eventuale presenza di attrito e dalla sua entità).

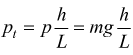
Si tratta di una forza costante che ha direzione costante lungo la direzione del piano inclinato. per la seconda legge della dinamica (F=ma) il grave si muove con accelerazione costante lungo la direzione del piano, verso il basso.

      

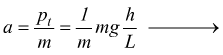
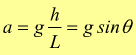
Chiaramente al termine della discesa il sistema di forze si ricompone, diventando p_n=p e p_t=0.
Se p_t=0 → a=0 ma sappiamo che a=Δv/t=0 → Δv=0 :il corpo continuerà a muoversi lungo la direzione orizzontale a velocità costante con moto uniforme. Questo, se non c'è attrito, altrimenti la forza di attrito R=f_d·p che si oppone al moto imprimerà una decelerazione al corpo.

Nello schema 100px=1m e si ipotizza assenza di attrito.