Velocità di un’onda

    

Il seguente disegno mostra due istantanee di un onda che viaggia in direzione positiva dell’asse x (verso destra).
Per definizione il rapporto incrementale Δx/Δt (o al limite differenziale dx/dt) rappresenta la velocità dell’onda che chiamiamo v.

Mentre l’onda si muove, ciascun punto, come ad esempio il punto P ce si trova sulla cresta, mantiene invariata la sua posizione y. Se il punto P mantiene la sua posizione al propagarsi dell’onda la fase dell’equazione caratteristica di un’onda in moto:
      X
deve mantenersi costante, cioè $kx-ωt=cost.$

anche se sia x che t variano costantemente. Derivando l'eq.precedente rispetto al tempo si ha:

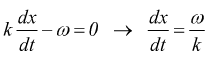   dunque  
    Y

usando poi le relazioni trovate nella pagina dei parametri ,  $k={2π}/λ$ e $ω={2π}/T$ si ha:

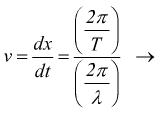
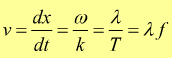       Z

Dunque, per trovare la velocità di un'onda basta dividere la lunghezza d'onda per il suo periodo. L'equazione

$$y(x,t)=y_m sin(kx-ωt)$$

descrive un'onda che si muove nel verso di x crescente. Per trovare l'equazione descrittiva di un'onda che si muove in senso opposto bisogna sostituire con -t il valore di t nell'eq. precedente ottenendo: $kx+ωt=cost.$; derivando rispetto al tempo si ha:

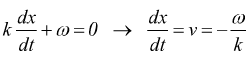
il segno negativo indica, appunto, che l'onda si propaga nel senso negativo di x.

L'equazione X non è l'unica espressione matematica che può descrivere un'onda in movimento. Qualsiasi funzione del tipo

può essere rappresentativa di un'onda in moto, come ad es. $y(x,t)=√^3{ab}$ oppure $y(x,t)=ln(ax+bt+c)$ con a b e c costanti. Per contro un’espressione del tipo $y(x,t)=sin(ax^2+bt)$ non è rappresentativa di un’onda in movimento.In particolare, ricordando l’identità

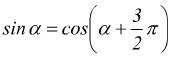
possiamo esprimere l'eq. X anche in funzione del coseno cioè:

è sempre e comunque un'onda in moto, che in virtù dell'identità $cosα=cos(-α)$ risulta esprimibile come

Consideriamo una generica perturbazione che nell'istante t=0 risulta rappresentabile come ne disegno seguente:

Si tratta di una curva che ha la sua cuspide per x=0.

supponendo che questa perturbazione si sposti nella direzione positiva dell'asse x con velocità costante v, in un generico istante t successivo a t=0 potremo avere la situazione seguente :

In tale istante l'onda avrà percorso la distanza x=vt che è poi la coordinata della cuspide della curva. Si deduce che se la perturbazione si muove con velocità v nel tempo, tale curva deve essere espressa dalla funzione :

consideriamo ora la funzione sinusoidale

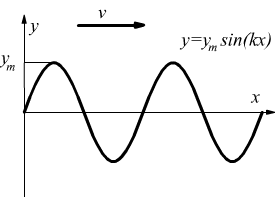
se viaggia in direzione positiva dell'asse x deve essere essere esprimibile come

dalla pagina sui parametri dell'onda abbiamo $$v=ω/k$$ dunque,

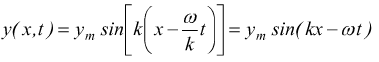
e ritroviamo l'eq. X.

Velocità di una corda tesa

    

La velocità di un'onda non solo dipende dalla lunghezza d'onda e alla frequenza di oscillazione come espresso dall'equazione Z, ma dipende anche dalle proprietà del mezzo. Se un'onda si muove in un mezzo come l'acqua, l'aria, il calcestruzzo, o su una corda tesa, deve fare oscillare le particelle di quel mezzo mentre lo attraversa. Affinché questo avvenga, il mezzo deve possedere sia l'inerzia (per immagazzinare energia cinetica) sia l'elasticità (per immagazzinare energia potenziale). Queste due proprietà determinano la velocità con cui l'onda può viaggiare nel mezzo. Per trovare questa relazione ci concentriamo su un singolo impulso lungo la corda.

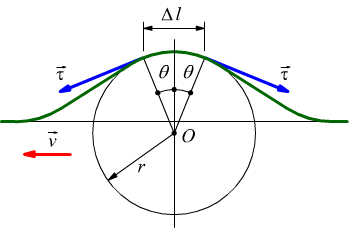
Consideriamo un piccolo segmento di lunghezza Δl della corda soggetta all'impulso, che forma un arco di circonferenza di raggio r e che sottende un angolo 2θ. Il tiro a cui è soggetta la corda τ agisce tangenzialmente sul segmento da ambo le parti. Le componenti orizzontali di queste forze si annullano, ma le componenti verticali si sommano per formare una nuova forza F radiale. La sua intensità sarà:

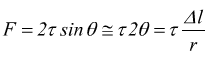    [ N ]

La massa del segmento può essere considerata come: $Δm=μΔl$ com μ massa lineica della corda.
Il segmento Δl si sta muovendo lungo un arco di circonferenza e sarà dunque dotato di accelerazione centripeta con μ massa lineica della corda. Il segmento Δl si sta muovendo lungo un arco di circonferenza e sarà dunque dotato di accelerazione centripeta $a=v^2/r$ dalla legge di Newton $F=m·a$ avremo :

     da questa equazione si trova la velocità

  [ m/s ]

La velocità di un'onda lungo una corda tesa ideale dipende soltanto dalla sua tensione e dalla sua massa lineica, e non dalla frequenza dell'onda. La frequenza dell'onda è completamente determinata da ciò che genera l'onda secondo la relazione $$λ=v/f$$.